Переменным называется ток, который изменяется с течением времени:
Мгновенным значением переменного тока называется его значение в фиксированный момент времени.
Периодическим называют такой переменный ток, мгновенные значения которого повторяются через равные промежутки времени:
![]() -- период переменного тока, т.е. наименьший промежуток времени,
по истечении которого мгновенные значения тока повторяются в той же последовательности.
-- период переменного тока, т.е. наименьший промежуток времени,
по истечении которого мгновенные значения тока повторяются в той же последовательности.
Простейшим типом периодического тока является гармонический ток:
| где | -- | амплитуда тока; | |
|
|
-- | полная фаза колебания; | |
| -- | начальная фаза колебания (при |
||
| -- | круговая частота (угловая скорость). |
![$\displaystyle \omega={2\pi\over T}=2\pi\nu\left[{Рад\over c}\right]\,,$](img13.png)
![$\displaystyle \nu={1\over T}[Гц]\,.$](img15.png)
Гармонический ток можно представить в виде проекции на вертикальную ось вращающегося вектора (рис.3.1).
Действующим или эффективным значением гармонического тока
называется значение такого постоянного тока, который протекая через одно
и тоже неизменное сопротивление ![]() за период времени
за период времени ![]() выделяет такое
же количество тепла, что и рассматриваемый гармонический ток.
выделяет такое
же количество тепла, что и рассматриваемый гармонический ток.
Между амплитудным и действующим значением гармонического тока существует простая связь:
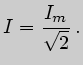
Аналогично для напряжения и ЭДС:
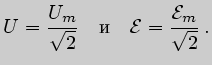
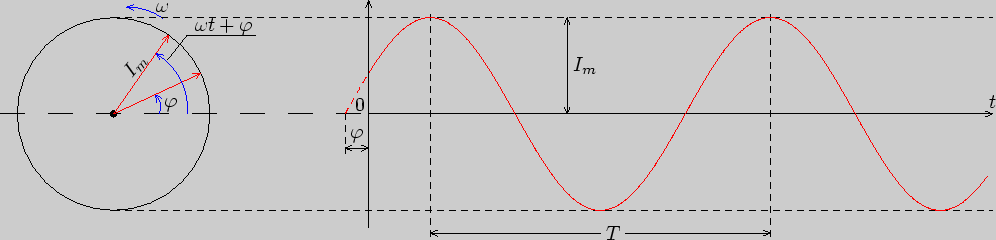
Рис. 3.1
Для мгновенных значений достаточно медленно изменяющихся переменных ЭДС и токов справедливы основные законы постоянного тока в их наиболее общей форме.
При этом следует иметь в виду, что сопротивление одной и той же электрической цепи для постоянного и переменного токов не совпадают. Так один и тот же резистор для постоянного и переменного токов имеет разное электрическое сопротивление.
Основными элементами электрической цепи переменного тока являются активное сопротивление, индуктивность и ёмкость.
Активное сопротивление представляет собой элемент электрической цепи, в котором при прохождении тока происходит необратимый процесс преобразования электрической энергии в тепловую.
Численное значение активного сопротивления определяется отношением мощности, расходуемой на тепло к квадрату действующего значения переменного тока:
![$\displaystyle R={P\over I^2}[Ом]\,.$](img20.png)
Необходимо помнить, что
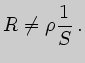
В цепи переменного тока с активным сопротивлением ток и напряжение совпадают по фазе (рис.3.2).

Рис. 3.2
Покажем это.
Пусть:
Начальная фаза тока
![]() .
.
Начальная фаза напряжения
![]() .
.
Разность фаз между напряжением и током:
В цепи с активным сопротивлением мгновенные, амплитудные и действующие значения напряжения и тока связаны законом Ома:
Индуктивность ![]() -- это элемент электрической цепи, способный
накапливать энергию магнитного поля.
-- это элемент электрической цепи, способный
накапливать энергию магнитного поля.
В цепи переменного тока с индуктивностью напряжение опережает по
фазе ток на
![]() (рис.3.3). Покажем это.
(рис.3.3). Покажем это.
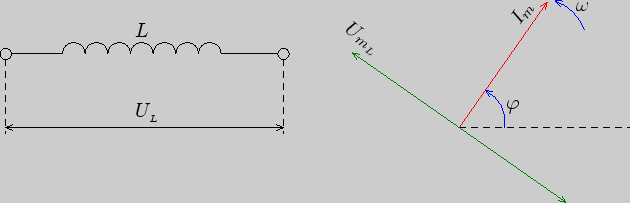
Рис. 3.3
Пусть
![]() .
.
При прохождении переменного тока в индуктивности возникает ЭДС самоиндукции:
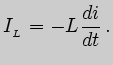
На основании закона Ома для участка цепи с ЭДС можно записать:

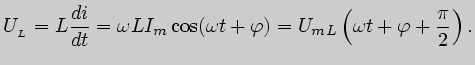
Начальная фаза тока
![]() .
.
Начальная фаза напряжения
![]() .
.
Разность фаз между напряжением и током:
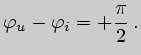
ЭДС самоиндукции отстаёт по фазе от тока на угол
![]() ,
так как
,
так как
![]() .
.
Таким образом, в цепи переменного тока с индуктивностью амплитудные и действующие значения напряжения и тока формально связаны законом Ома:
Ёмкость ![]() -- это элемент электрической цепи, способный накапливать
энергию электрического поля.
-- это элемент электрической цепи, способный накапливать
энергию электрического поля.
В цепи переменного тока с ёмкостью напряжение отстаёт по фазе от
тока на угол
![]() (рис.3.4). Докажем это.
(рис.3.4). Докажем это.
Пусть:
Это напряжение приложено к конденсатору от внешнего источника. Оно уравновешивает ЭДС ёмкости (аналогичную ЭДС самоиндукции в катушке индуктивности), которая возникает при наличии зарядов на обкладках конденсатора.
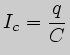
![\includegraphics[width=1.05\textwidth]{D:/html/work/link1/lab/lab_elekt19/lab_elekt19pic.4}](img49.png)
Рис. 3.4
На основании закона Ома для участка цепи с ЭДС можно записать:
За положительное направление тока в соответствии с законом сохранения электрического заряда принимается направление, при котором заряды покидают обкладки конденсатора:
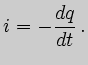
Вместе с тем
![]() .
.
Следовательно,
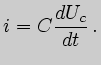
Подставляя значение ![]() , получим:
, получим:
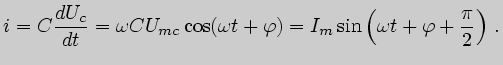
Начальная фаза напряжения
![]() .
.
Начальная фаза тока
![]() .
.
Разность фаз между напряжением и током:
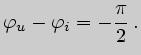
При этом ЭДС ёмкости опережает по фазе ток на угол
![]() . Таким образом, в цепи переменного
тока с ёмкостью амплитудные и действующие значения напряжения и тока
формально связаны законом Ома:
. Таким образом, в цепи переменного
тока с ёмкостью амплитудные и действующие значения напряжения и тока
формально связаны законом Ома:
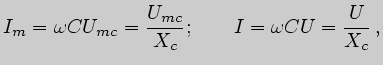
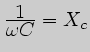 -- ёмкостное сопротивление,
измеряемое в [Ом].
-- ёмкостное сопротивление,
измеряемое в [Ом].
Это расчётная величина, которая не имеет физического смысла.
В общем случае в состав цепи переменного тока могут входить и активное сопротивление, и ёмкость, и индуктивность. Все эти элементы могут быть соединены между собой как последовательно, так и параллельно. На рисунке 3.5 показана схема последовательного соединения указанных элементов и соответствующая им векторная диаграмма для тока и напряжений.
![\includegraphics[width=1.12\textwidth]{D:/html/work/link1/lab/lab_elekt19/lab_elekt19pic.5}](img61.png)
Рис. 3.5
В цепи, состоящей из последовательно соединённых ![]() ,
, ![]() и
и ![]() через все элементы
протекает один и тот же ток:
через все элементы
протекает один и тот же ток:
Падение напряжения на элементах цепи:
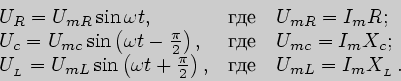
Приложенное мгновенное значение напряжения равно сумме мгновенных падений напряжения на отдельных элементах цепи:
Сложение этих гармонических напряжений произведено в векторной форме (рис.3.5). Порядок построения векторной диаграммы обозначен цифрами.
![]() -- активная составляющая напряжения.
-- активная составляющая напряжения.
![]() -- реактивная составляющая напряжения.
-- реактивная составляющая напряжения.
Из векторной диаграммы следует, что
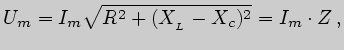
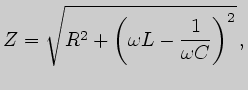
![]() -- активная составляющая сопротивления цепи;
-- активная составляющая сопротивления цепи;
![]() -- реактивная составляющая сопротивления цепи.
-- реактивная составляющая сопротивления цепи.
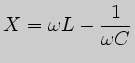
Условились индуктивное сопротивление считать положительным, а ёмкостное -- отрицательным.
Поэтому реактивное сопротивление цепи ![]() в зависимости от знака может иметь
либо индуктивный характер
в зависимости от знака может иметь
либо индуктивный характер
![]() , либо ёмкостный характер
, либо ёмкостный характер
![]() .
.
Реактивные сопротивления ![]() ,
, ![]() и
и ![]() зависят от частоты.
Соответствующие графики приведены на рисунке3.6.
зависят от частоты.
Соответствующие графики приведены на рисунке3.6.
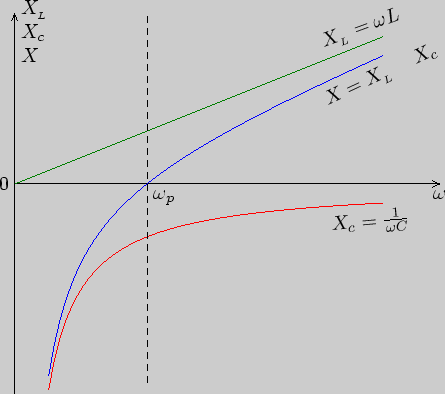
Рис. 3.6
В зависимости от знака реактивного сопротивления треугольники напряжений могут иметь вид:
![\includegraphics[width=1.05\textwidth]{D:/html/work/link1/lab/lab_elekt19/lab_elekt19pic.7}](img78.png)
Рис. 3.7
Угол ![]() положителен при отстающем и отрицателен при опережающем токе.
положителен при отстающем и отрицателен при опережающем токе.
Если все стороны треугольников напряжений (рис.3.7) разделить на амплитуду тока, то получатся соответствующие треугольники сопротивлений (рис.3.8).
Угол ![]() всегда отсчитывается от
всегда отсчитывается от ![]() к
к ![]() .
.
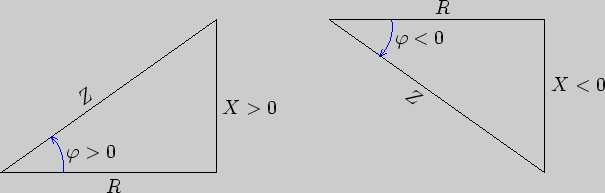
Рис. 3.8
Из треугольников сопротивлений (рис.3.8) следует ряд важных соотношений:
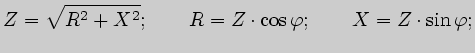
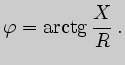
На частоте
![]() полное реактивное сопротивление
цепи становится равным нулю и цепь из
полное реактивное сопротивление
цепи становится равным нулю и цепь из ![]() ,
, ![]() и
и ![]() ведёт себя как чисто активное сопротивление:
ведёт себя как чисто активное сопротивление:
| где | -- | активное сопротивление катушки индуктивности; | |
| -- | активное сопротивление конденсатора; | ||
| -- | активное сопротивление внешнего резистора. |
Состояние электрической цепи на частоте ![]() носит название резонанса напряжений.
носит название резонанса напряжений.
Работа в цепи переменного тока за время одного периода ![]() выражается формулой:
выражается формулой:
Средняя за период мощность называется активной мощностью:
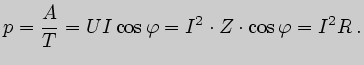
Она расходуется в активном сопротивлении цепи переменного тока.
Наряду с изложенным необходимо иметь в виду, что любая реальная катушка индуктивности как и любой реальный конденсатор при работе в цепи переменного тока имеют не только реактивные, но и активные сопротивления. На рисунке3.9 показаны реальные катушка индуктивности и конденсатор и их эквивалентные схемы:
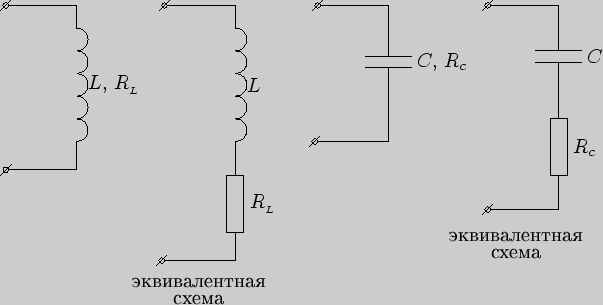
Рис. 3.9