Далее: 2.  Описание установки Вверх: Лабораторная работа 7 Назад: Лабораторная работа 7

1.  Теоретическое введение

Механическими колебаниями, движениями называется движение, обладающее той или иной степенью повторяемости.

Колебания, при которых состояние движения точно повторяется через определённые промежутки времени, называются периодическими. Среди многообразия колебательных движений особое место занимают гармонические колебания. Изучение этих колебаний занимает особое место, так как к ним может быть сведён большой класс колебательных движений. Простейшим примером гармонического колебания является движение так называемого математического маятника. Математический маятник представляет собой абстракцию: на невесомой нерастяжимой нити висит материальная точка (тело, имеющее массу, но не имеющее размеров). Центр тяжести такой системы будет совпадать с центром тяжести материальной точки. Практически такой маятник создать невозможно, но маленький шарик, подвешенный на нити, размеры которой во много раз больше размеров шарика, по своим свойствам близок к математическому. Такая система, выведенная из положения равновесия на малый угол совершает гармонические колебания.

Колебания маятника совершаются по определённому закону. Закон колебания маятника это зависимость $S$ от $t$, где $S$-дуговое смещение маятника от положения равновесия (рис.1.1)

Для получения закона колебания используем уравнение движения Ньютона:

$$\sum\limits_{i=1}^n \vec{F_i}=m\vec{a}$$

на шарик маятника действует сила тяжести $\vec{P}$ и $\vec{N}$ сила натяжения нити.

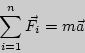
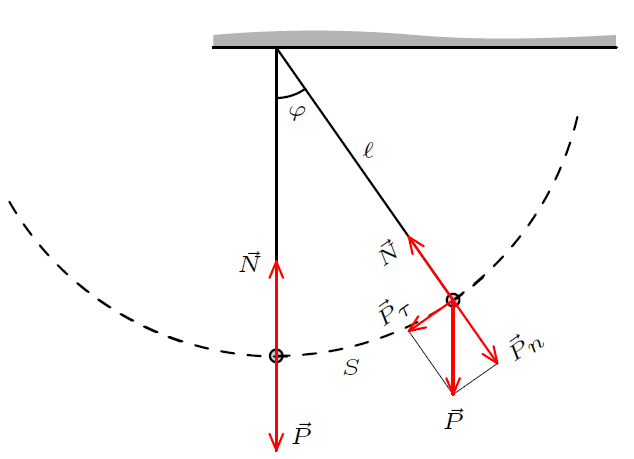
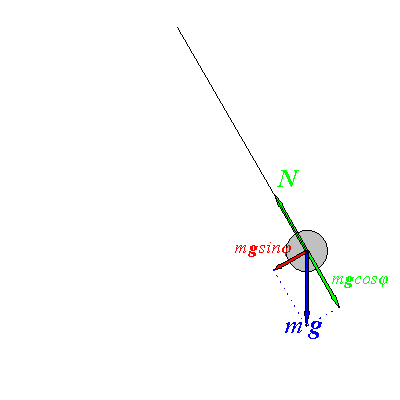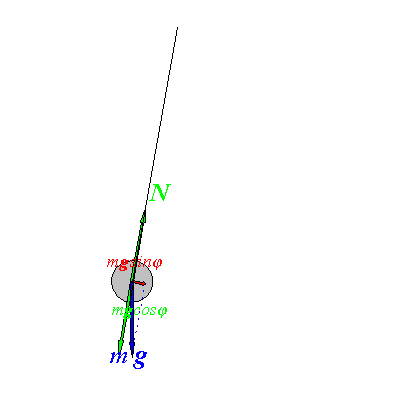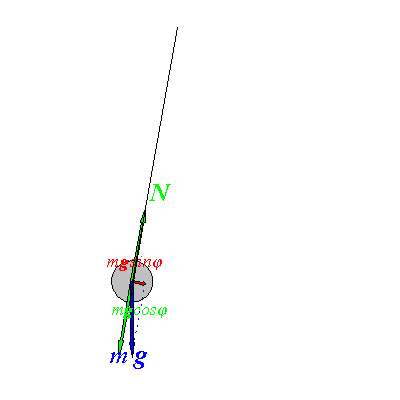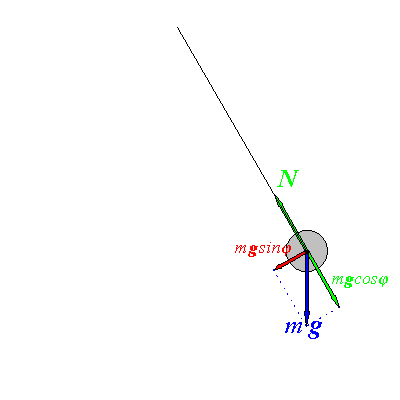
Рис. 1.1 

Выведем маятник из положения
равновесия на малый угол $\varphi$.

Разложим силу $\vec{P}$ на две составляющие $\vec{P}_{n}$ и $\vec{P}_{\tau}$. Сила $\vec{P}_{\tau}$ обеспечивает колебания маятника. Модуль этой силы равен $-P\sin\varphi\approx -P{S\over\ell}$. Используя закон Ньютона, получим: $a_{t}m=-P{S\over\ell}$. Поскольку $a=S''(t)$, a $P\approx mg$, то

$$S''(t)=-\frac{g}{\ell}S(t) .$$ (1)

Это дифференциальное уравнение гармонического колебания. Где $\frac{g}{\ell}=\omega^2$, $\omega$ -- собственная циклическая частота гармонического колебания. Решение этого уравнения даёт закон колебания математического маятника $S=S_o\cos(\omega t+\varphi_o)$, где $S_o$ -- амплитуда колебания (максимальное смещение маятника от положения равновесия).

Зная частоту $\omega$, можно вычислить период (время одного полного колебания) собственных колебаний маятника $T$:

$$T=\frac{2\pi}{\omega};\qquad T=2\pi\sqrt{\frac{\ell}{g}} .$$ (2)

Зависимость (2) позволяет определить $g$ -- ускорение свободного падения в данном месте Земли по известному периоду колебаний.

Практически, всякое реальное колебание происходит с постепенным расходованием энергии движения на работу против сил сопротивления. При этом амплитуда и скорость колебательного движения убывают.

Происходит затухание колебаний. В этом случае колебания уже не будут гармоническими, так как у них меняется амплитуда колебаний и частота, что приводит к изменению периода колебаний.

Практически, наибольший интерес представляют случаи колебаний с небольшими скоростями, при которых сила сопротивления пропорциональна скорости $\vec{v}$: $\vec{F}_{\text{сопр.}}=r\vec{v}$. Где $r=const$ -- коэффициент сопротивления. В этом случае уравнение движения маятника запишется так:

$$S''(t)=-\frac{g}{\ell}S(t)-\frac{r}{m}S'(t) ,$$

т.е. помимо силы $\vec{P}_{\tau}$ на тело действует сила сопротивления $\vec{F}_{\text{сопр.}}$. Решением этого уравнения является функция вида:

$$S(t)=S_o e^{-\frac{r}{2m}t}\cos(\omega t+\varphi_o)$$ (3)

или, введя обозначения $S_o e^{-\beta t}=S_m(t)$; где $\beta=\frac{r}{2m}$, получим:

$$S(t)=S_m(t)\cdot\cos(\omega t+\varphi_o) .$$

Из уравнения (3) видно, что амплитуда колебаний уменьшается со временем по экспоненциальному закону (рис.1.2).

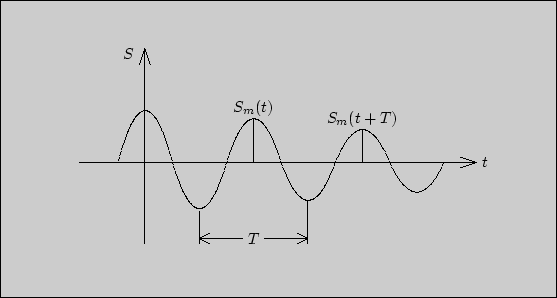
Рис. 1.2 

Отношение амплитуд, отстоящих друг от друга по времени на период колебаний, называется декрементом затухания.

$$\frac{S_m(t)}{S_m(t+T)}=\frac{S_o e^{-\beta t}}{S_o e^{-\beta(t+ T)}}=\frac{1}{e^{-\beta T}}=e^{\beta T}$$

Из этого соотношения видно, что отношение амплитуд затухающих колебаний, отстоящих друг от друга на интервал времени, равный периоду, постоянно во всё время колебаний.

Натуральный логарифм этого отношения называется логарифмическим декрементом затухания $\alpha$.

$$\alpha=\ln\frac{S_m(t)}{S_m(t+T)}=\beta T ,$$ (4)

где $\beta$ -- коэффициент затухания, $\beta=\frac{\alpha}{T}$.

Логарифмический декремент затухания характеризует быстроту убывания амплитуды и зависит от $r$ коэффициента сопротивления среды и массы системы.

Далее: 2.  Описание установки Вверх: Лабораторная работа 7 Назад: Лабораторная работа 7