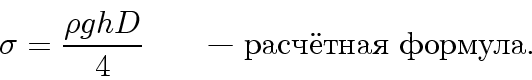В узких трубках (капиллярах), опущенных в жидкость, хорошо заметно
поднятие или опускание жидкости. Поверхностная пленка жидкости в
трубке под действием молекулярных сил жидкости и твердого тела
принимает вогнутую или выпуклую форму (рис.1). По
величине ![]() подъёма или опускания жидкости можно определить
коэффициент поверхностного натяжения. Такой метод и используется в
данной работе.
подъёма или опускания жидкости можно определить
коэффициент поверхностного натяжения. Такой метод и используется в
данной работе.
Давление под искривленной поверхностью жидкости больше или меньше,
чем под горизонтальной, на величину добавочного давления
(Лапласа), которое для произвольной кривизны поверхности
рассчитывается по формуле:
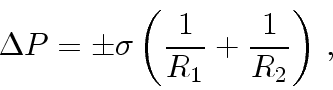
Давление Лапласа направлено по радиусу к центру кривизны. В случае
смачивающей жидкости давление внутри трубки меньше, чем снаружи,
поэтому жидкость в ней поднимается до тех пор, пока
гидростатическое давление столбика жидкости не уравновесит
давление Лапласа. Для сферической поверхности жидкости 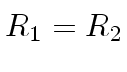 и
и
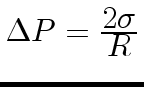 .
.
Тогда
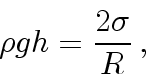
| где | -- | плотность жидкости, | |
| -- | высота уровня жидкости в трубке относительно | ||
| уровня в сосуде, | |||
| -- | радиус кривизны поверхности жидкости. |
Если диаметр трубки равен ![]() , то он связан с радиусом следующим
соотношением:
, то он связан с радиусом следующим
соотношением:
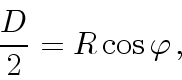
Тогда выражение для коэффициента поверхностного натяжения будет
иметь вид:
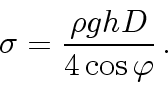
Практически измерить краевой угол трудно. Если жидкость вполне
смачивает поверхность капилляра, то краевой угол равен нулю. В
этом случае выражение для расчета коэффициента поверхностного
натяжения примет вид: