Далее: 2.2.  Интерференция от многих Вверх: 2.  Теоретическое введение Назад: 2.  Теоретическое введение

2.1.  Дифракция на щели

Пусть плоская монохроматическая волна падает на экран с узкой бесконечно длинной щелью. На рис. 1 $FF_{1}$ -- проекция экрана со щелью $AB$ на плоскость рисунка. Ширина щели ($b$) имеет размер порядка длины волны света. Щель $AB$ вырезает часть фронта падающей световой волны. Все точки этого фронта колеблются в одинаковых фазах и на основании принципа Гюйгенса-Френеля, являются источниками вторичных волн.

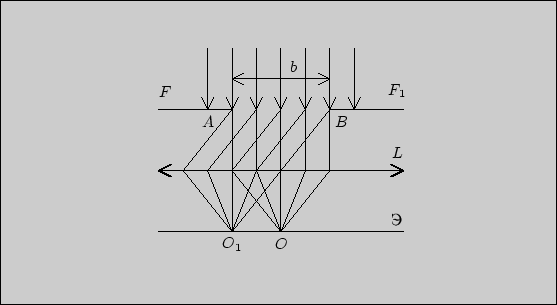
Рис. 1 

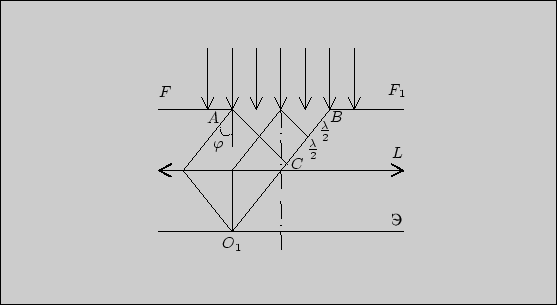
Рис. 2 

Вторичные волны распространяются по всем направлениям от (0) до ( $\pm{\pi \over 2}$) к направлению распространения волн (рис. 1). Если за щелью поставить линзу, то все лучи, которые шли до линзы параллельно, соберутся в одной точке фокальной плоскости линзы. В этой точке наблюдается интерференция вторичных волн. Результат интерференции зависит от числа длин полуволн, которое укладывается в разности хода между соответствующими лучами.

Рассмотрим лучи, которые идут под некоторым углом $\varphi$ к направлению падающей световой волны (рис. 2). $BC=\delta$ -- разность хода между крайними лучами. Разобьем $AB$ на зоны Френеля (зоны Френеля в данном случае представляют собой систему параллельных плоскостей, перпендикулярных плоскости рисунка и построенных так, что расстояние от краев каждой зоны до точки $O_1$ отличается на $\lambda\over 2$).

Если в $\delta$ уложиться четное число длин полуволн, то в точке $O_1$ будет ослабление света -- $min$. Если нечетное, то усиление света -- $max$.

$$\begin{array}{rrclclllll} \text{Следовательно, при } & \delta... ...\pm(2m+1){\lambda\over 2}&\Rightarrow & max & & & & \end{array}$$

где m = 0; 1; 2; ...

Поскольку $\delta=b\cdot\sin\varphi$ (см. рис. 2), то эти условия можно записать в следующем виде:

$$b\cdot\sin\varphi=\pm 2m{\lambda\over 2} \Rightarrow min$$ (1)

$$b\cdot\sin\varphi=\pm(2m+1){\lambda\over 2} \Rightarrow max$$ (2)

На рис. 3 дано распределение интенсивности света при дифракции на щели в зависимости от угла. Её можно вычислить по формуле:

$$I_{\varphi}=I_{o}{\sin^{2}(\pi\cdot b\cdot\sin{\varphi\over\lambda})\over(\pi \cdot b\cdot\sin{\varphi\over\lambda})^{2}}$$

где	$I_{o}$	-	интенсивность в середине дифракционной картины;
	$I_{\varphi}$	-	интенсивность в точке, определяемой значением.

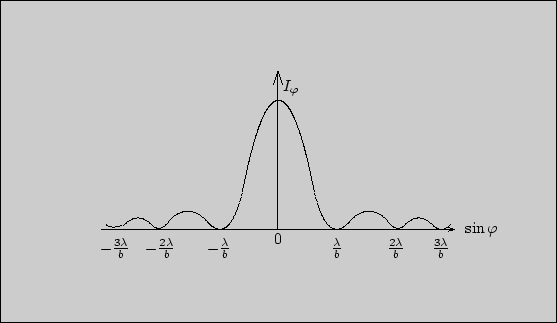
Рис. 3 

Далее: 2.2.  Интерференция от многих Вверх: 2.  Теоретическое введение Назад: 2.  Теоретическое введение