Задание 21.
Точечный заряд ![]() находится в центре сферической
поверхности. Если
добавить заряд
находится в центре сферической
поверхности. Если
добавить заряд ![]() за пределами сферы, то поток
вектора
напряженности электростатического поля
за пределами сферы, то поток
вектора
напряженности электростатического поля ![]() через поверхность
сферы...
через поверхность
сферы...
Варианты ответов:
1) уменьшится; 2) увеличится; 3) не изменится.
Решение: Поток вектора напряженности электростатического
поля
через замкнутую поверхность сферы равен алгебраической сумме
зарядов, заключенных внутри этой поверхности, деленной на
![]() :
:
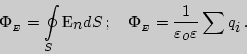
Поскольку добавленный заряд находится вне сферы, то поток не изменится.
Ответ: не изменится.
Задание 22.
Дана система точечных зарядов в вакууме и замкнутые поверхности ![]() ,
, ![]() ,
, ![]() . Поток
вектора напряженности электростатического
поля равен
. Поток
вектора напряженности электростатического
поля равен ![]() через поверхность...
через поверхность...
![\includegraphics[width=0.7\textwidth]{D:/html/work/link1/metod/met108/posobiepic.10}](img183.png)
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Решение: Из рисунка видим, что поверхность ![]() не
охватывает зарядов (внутри замкнутой поверхности нет зарядов),
следовательно, поток вектора напряженности через эту поверхность
равен
не
охватывает зарядов (внутри замкнутой поверхности нет зарядов),
следовательно, поток вектора напряженности через эту поверхность
равен ![]() .
.
Ответ: ![]() .
.
Задание 23.
Поле создано бесконечной равномерно заряженной плоскостью с
поверхностной плотностью заряда ![]() . Укажите направление
вектора градиента потенциала в точке
. Укажите направление
вектора градиента потенциала в точке ![]() .
.
![\includegraphics[width=0.7\textwidth]{D:/html/work/link1/metod/met108/zad23.eps}](img186.png)
Варианты ответов: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)
![]() .
.
Решение: В электростатическом поле напряженность равна
градиенту потенциала, взятому с обратным знаком:
![]() .
Знак ''
.
Знак ''![]() '' отражает тот факт, что векторы
'' отражает тот факт, что векторы ![]() и
и
![]() направлены
противоположно.
направлены
противоположно.
В случае положительно заряженной плоскости градиент потенциала
направлен против силовой линии, то есть в направлении ![]() . Если бы
плоскость имела отрицательный заряд, то это было бы направление
. Если бы
плоскость имела отрицательный заряд, то это было бы направление ![]() .
.
Ответ: ![]() .
.
На рисунке представлена зависимость плотности тока ![]() , протекающего
в проводниках 1 и 2, от напряженности электрического поля
, протекающего
в проводниках 1 и 2, от напряженности электрического поля ![]() .
.
![\includegraphics[width=0.7\textwidth]{D:/html/work/link1/metod/met108/zad24.eps}](img196.png)
Отношение удельных проводимостей
![]() этих элементов
равно...
этих элементов
равно...
Варианты ответов: 1) 1/2; 2) 2; 3) 1/4; 4) 4.
Решение: Закон Ома в дифференциальной форме имеет вид:
![]() . Используя данные,
представленные на
графике, определим в условных единицах удельные проводимости для
первого и второго проводников и найдем их отношение:
. Используя данные,
представленные на
графике, определим в условных единицах удельные проводимости для
первого и второго проводников и найдем их отношение:
На рисунке изображены сечения двух параллельных прямолинейных
длинных проводников с противоположно направленными токами, причем ![]() . Индукция результирующего магнитного поля
равна нулю в
некоторой точке интервала...
. Индукция результирующего магнитного поля
равна нулю в
некоторой точке интервала...
![\includegraphics[width=0.7\textwidth]{D:/html/work/link1/metod/met108/zad25.eps}](img216.png)
Варианты ответов: 1) ![]() ; 2)
; 2)
![]() ; 3)
; 3) ![]() ; 4)
; 4)
![]() .
.
Решение: Магнитное поле в интервалах ![]() ,
, ![]() ,
, ![]() ,
, ![]() образовано в результате наложения (суперпозиции) полей, созданных
прямолинейными длинными проводниками с токами
образовано в результате наложения (суперпозиции) полей, созданных
прямолинейными длинными проводниками с токами ![]() и
и ![]() . В
соответствии с законом Био-Савара-Лапласа магнитная индукция поля
прямого тока определяется выражением:
. В
соответствии с законом Био-Савара-Лапласа магнитная индукция поля
прямого тока определяется выражением:
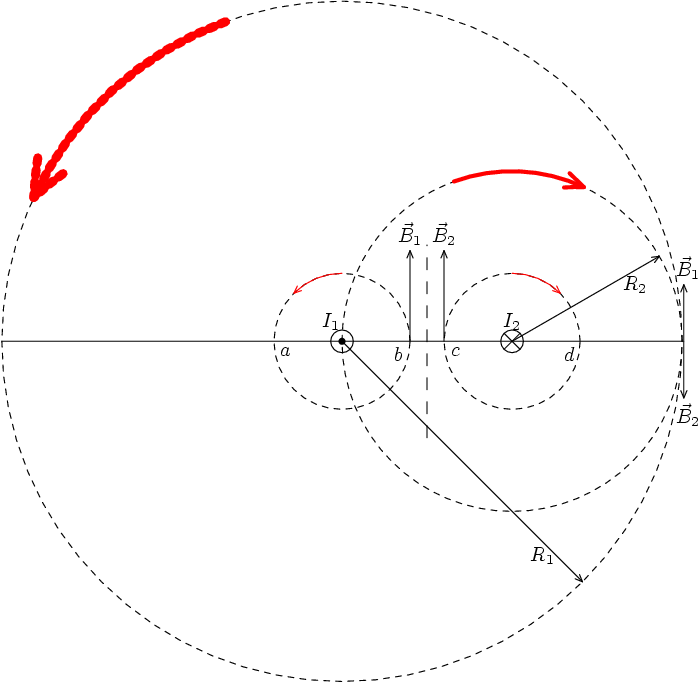
В областях ![]() и
и ![]() касательные к силовым линиям направлены в
противоположные стороны, и магнитные поля могут друг друга
компенсировать, если модули векторов
касательные к силовым линиям направлены в
противоположные стороны, и магнитные поля могут друг друга
компенсировать, если модули векторов ![]() и
и ![]() будут
равны.
будут
равны.
Запишем выражение для молулей ![]() и
и ![]() с учетом
данных задачи (
с учетом
данных задачи (![]() ).
).
Сравнивая выражения для ![]() и
и ![]() , можно
сделать вывод, что
модули этих векторов будут равны при
, можно
сделать вывод, что
модули этих векторов будут равны при ![]() , то
есть расстояние
от тока
, то
есть расстояние
от тока ![]() в 2 раза больше до искомой точки, чем от
в 2 раза больше до искомой точки, чем от ![]() . Эта
точка находитcя в интервале
. Эта
точка находитcя в интервале ![]() .
.
Ответ: интервал ![]() .
.
Дополнение.
В условии задачи 25 изменим направление одного из токов и
определим интервал, в котором результирующее магнитное поле равно
нулю, если поле создается двумя длинными параллельными
прямолинейными проводниками с одинаково направленными токами, причем ![]() .
.
В этом случае искомая точка будет находиться в интервале ''![]() ''.
''.
В этом интервале вектора ![]() и
и ![]() направлены
противоположно. Для равенства модулей этих векторов необходимо,
чтобы
направлены
противоположно. Для равенства модулей этих векторов необходимо,
чтобы ![]() , то есть точка будет находиться ближе к току
, то есть точка будет находиться ближе к току ![]() , это интервал ''
, это интервал ''![]() ''.
''.
Задание 26.
Относительно статических электрических полей
справедливы
утверждения:
Варианты ответов:
1) Электростатическое поле совершает работу над электрическим зарядом.
2) Электростатическое поле является вихревым.
3) Силовые линии поля разомкнуты
1) Электростатическое поле совершает работу над электрическим зарядом;
3) Силовые линии поля разомкнуты.
Второе утверждение относится к магнитному полю: магнитное поле является вихревым, линии магнитной индукции поля замкнуты.
Ответ: варианты 1 и 3.
Задание 27.
На рисунке представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре не возникает на интервале...
![\includegraphics[width=1.1\textwidth]{D:/html/work/link1/metod/met108/zad27.eps}](img222.png)
Варианты ответов:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)
![]() ; 4)
; 4) ![]() ; 5)
; 5)
![]() .
.
Решение: Согласно закону электромагнитной индукции
Фарадея,
ЭДС индукции:
Ответ: интервал ![]() .
.
Задание 28 (выберите один вариант ответа).
В магнитное поле, изменяющееся по закону
![]() ,
помещена квадратная рамка со стороной
,
помещена квадратная рамка со стороной
![]() . Нормаль к
рамке совпадает с направлением изменения поля. ЭДС индукции,
возникающая в рамке, изменяется по закону...
. Нормаль к
рамке совпадает с направлением изменения поля. ЭДС индукции,
возникающая в рамке, изменяется по закону...
Варианты ответов:
1) ![]() ; 2)
; 2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
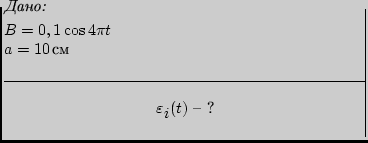 Решение:
ЭДС индукции, возникающую в рамке, определим по
закону Фарадея для электромагнитной индукции:
Решение:
ЭДС индукции, возникающую в рамке, определим по
закону Фарадея для электромагнитной индукции:
Ответ:
![]()
Задание 29.
Полная система уравнений Максвелла для электромагнитного поля имеет вид:
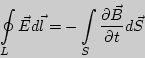
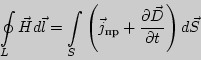
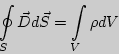
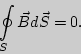
Следующая система уравнений:
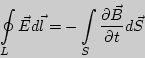
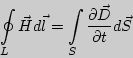
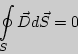
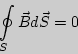
Варианты ответов:
1) в отсутствие заряженных тел и токов проводимости;
2) в отсутствие токов проводимости;
3) при наличии заряженных тел и токов проводимости
4) в отсутствие заряженных тел.
Решение: В отсутствии заряженных тел
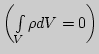 и токов проводимости
и токов проводимости
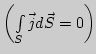 полная система
уравнений Максвелла для электромагнитного поля принимает указанный
вид. (И.В.Савельев. ''Курс общей физики'' т.2, 1978г.,
стр.198-200 и 295.)
полная система
уравнений Максвелла для электромагнитного поля принимает указанный
вид. (И.В.Савельев. ''Курс общей физики'' т.2, 1978г.,
стр.198-200 и 295.)
Ответ: вариант 1.
Задание 30 (выберите один вариант ответа).
Утверждение: ''В любой точке пространства изменяющееся магнитное поле возбуждает вихревое электрическое поле'' раскрывает физический смысл уравнения...
Варианты ответов:
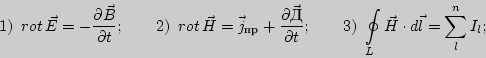
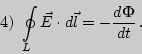
Ответ: вариант 1.