В ряде уравнений и неравенств некоторые коэффициенты могут быть обозначены буквами. Такие буквы называются параметрами. При подстановке вместо этих букв конкретных числовых значений уравнение или неравенство будет содержать только числовые коэффициенты. Тем самым параметр позволяет найти общее решение семейства однотипных уравнений или неравенств.
Решение задачи с параметром предполагает реализацию следующего плана:
1. Найти области определения основной переменной и параметра.
2. Найти контрольные значения параметра.
3. Определить, при каком значении параметра уравнение или неравенство имеет решение; представить общий вид решения в виде формулы; указать количество решений в зависимости от значений параметра.
Задачи с параметром могут решаться аналитически и графически.
Примеры:
1. При каких значениях параметра уравнение
![]() имеет два различных
отрицательных корня?
имеет два различных
отрицательных корня?
![]() : Уравнение имеет два различных корня при положительном дискриминанте:
: Уравнение имеет два различных корня при положительном дискриминанте:
![]() .
.
Если оба корня уравнения отрицательны, то по теореме Виета:
Составим систему условий для параметра:
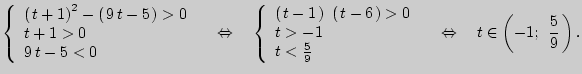
Ответ:
![]() .
.
2. Решить уравнение
![]() . Указать количество
решений уравнения в зависимости от значений параметра
. Указать количество
решений уравнения в зависимости от значений параметра ![]() .
.
Решение: основная переменная ![]() и параметр
и параметр ![]() могут быть любым действительным числом.
Обозначим
могут быть любым действительным числом.
Обозначим ![]() .
.
Тогда исходное уравнение примет вид:
![]() .
.
а) Исходное уравнение будет иметь 2 корня, если ![]() и
и ![]() положительны:
положительны:
![]() . Вспомогательное квадратное уравнение всегда имеет 2 корня:
. Вспомогательное квадратное уравнение всегда имеет 2 корня:
![]() Оба корня больше нуля при
Оба корня больше нуля при ![]() .
.
Тогда получаем:
![]() .
.
б) Исходное уравнение будет иметь 1 корень, если меньший из корней вспомогательного уравнения отрицателен или равен нулю, а второй - больше нуля:
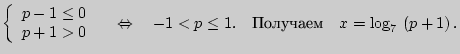
в) Если оба корня вспомогательного уравнения отрицательны или равны нулю, то исходное уравнение не имеет корней:
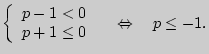
Ответ: если ![]() , уравнение не имеет решений;
, уравнение не имеет решений;
если
![]() , уравнение имеет один корень
, уравнение имеет один корень
![]() ;
;
если ![]() , уравнение имеет два корня:
, уравнение имеет два корня:
![]() .
.
3. Решить неравенство
![]() .
.
Решение: а) При ![]() = 0 получим неравенство
= 0 получим неравенство
![]() , верное при любом
действительном
, верное при любом
действительном ![]() .
.
б) Если ![]() , исходное неравенство равносильно неравенству
, исходное неравенство равносильно неравенству
![]() , решение которого принадлежит промежутку
, решение которого принадлежит промежутку
![]() .
.
в) Если ![]() , исходное неравенство равносильно неравенству
, исходное неравенство равносильно неравенству
![]() , справедливому при всех действительных
, справедливому при всех действительных ![]() .
.
Ответ: если ![]() , то
, то
![]() ; если
; если ![]() , то
, то
![]() .
.
4. Найти все значения ![]() , при которых уравнение
, при которых уравнение
![]() имеет решение, принадлежащее отрезку
имеет решение, принадлежащее отрезку
![]() .
.
Решение: Перепишем уравнение в виде
![]() .
.
Рассмотрим функцию
![]() и найдем множество ее значений на отрезке
и найдем множество ее значений на отрезке
![]() , используя понятие производной
, используя понятие производной
![]() ; функция
; функция
![]() имеет экстремумы при
имеет экстремумы при
![]() ;
;
![]() ;
; ![]() и
и ![]() принадлежат отрезку
принадлежат отрезку
![]() . В
точке
. В
точке ![]() = 1 функция
= 1 функция
![]() имеет локальный максимум
имеет локальный максимум
![]() ; в точке
; в точке ![]() = 3 функция
= 3 функция
![]() имеет минимум
имеет минимум
![]() .
.
На концах отрезка функция принимает следующие значения:
![]() .
.
Таким образом, на отрезке
![]()
![]() принимает значения из отрезка
принимает значения из отрезка
![]() . Следовательно, если параметр
. Следовательно, если параметр ![]() будет принимать
значения из отрезка
будет принимать
значения из отрезка
![]() , то
исходное уравнение будет иметь решение, принадлежащее отрезку
, то
исходное уравнение будет иметь решение, принадлежащее отрезку
![]() . При других значениях параметра
требования задачи не будут выполнены.
. При других значениях параметра
требования задачи не будут выполнены.
Эту же задачу можно решить графическим методом, построив графики функций
![]() и
и
![]() и рассмотрев их поведение на отрезке
и рассмотрев их поведение на отрезке
![]() .
.