1. Задачи на совместную работу
Задача 1. Две копировальные машины печатают рукопись. Если всю рукопись будет печатать первая машина, то работа будет выполнена на 4 минуты позже, чем двумя машинами, работающими вместе. Если печатать всю рукопись будет вторая машина, то она напечатает на 25 минут позже, чем обе машины, работающие вместе. За сколько минут может напечатать эту рукопись вторая машина?
Решение:
1 способ. Примем за единицу работу по печати всей рукописи. Пусть время
печати всей рукописи первой машиной ![]() (мин.), а второй
(мин.), а второй ![]() (мин.). Тогда
производительность первой машины
(мин.). Тогда
производительность первой машины
![]() , производительность второй
машины
, производительность второй
машины
![]() ; общая производительность двух машин
; общая производительность двух машин
![]() , а время их совместной работы
, а время их совместной работы
![]() . Теперь можно составить два уравнения
относительно времени работы:
. Теперь можно составить два уравнения
относительно времени работы:
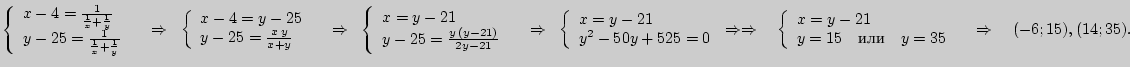
В соответствии с условиями задачи решение (- 6; 15) является посторонним. Следовательно, вторая машина может напечатать всю рукопись за 35 минут.
2 способ. Пусть время печати всей рукописи первой машиной ![]() (мин.), а второй
(мин.), а второй
![]() (мин.). Тогда время совместной работы двух машин можно найти двумя
способами:
(мин.). Тогда время совместной работы двух машин можно найти двумя
способами:
![]() - 4 и
- 4 и ![]() - 25. Таким образом, получаем первое уравнение:
- 25. Таким образом, получаем первое уравнение:
![]() .
.
Примем за единицу работу по печати всей рукописи. Тогда производительность
первой машины
![]() , производительность второй машины
, производительность второй машины
![]() ,
общая производительность двух машин
,
общая производительность двух машин
![]() . Зная их общее время работы (
. Зная их общее время работы (![]() - 4), можно составить второе
уравнение
- 4), можно составить второе
уравнение
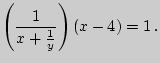
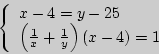
Ответ: 35 минут.
Задача 2. Если две трубы открыть одновременно, то бассейн наполнится за 2 часа 24
минуты. В действительности же сначала была открыта только первая труба в
течение одной четверти времени, которое необходимо второй трубе, чтобы
наполнить бассейн, если она будет действовать отдельно. Затем действовала
вторая труба, также в течение одной четверти времени, которое необходимо
первой трубе, чтобы одной наполнить бассейн. После чего оказалось, что
осталось наполнить
![]() полной вместимости бассейна. Сколько
времени необходимо для наполнения бассейна каждой трубой в отдельности?
полной вместимости бассейна. Сколько
времени необходимо для наполнения бассейна каждой трубой в отдельности?
Решение: Пусть время наполнения бассейна первой трубой ![]() часов, второй
часов, второй ![]() часов, тогда
производительность каждой трубы будет соответственно
часов, тогда
производительность каждой трубы будет соответственно
![]() и
и
![]() в час. Из условия следует, что первая труба наполнила
в час. Из условия следует, что первая труба наполнила
![]() часть бассейна, вторая
часть бассейна, вторая
![]() часть бассейна, а вместе они наполнили
часть бассейна, а вместе они наполнили
![]() части бассейна. Отсюда
части бассейна. Отсюда
![]() . Так как обе трубы при
одновременной работе наполняют бассейн за 2 часа 24 минуты, то
. Так как обе трубы при
одновременной работе наполняют бассейн за 2 часа 24 минуты, то
![]() . Теперь составим
и решим систему уравнений:
. Теперь составим
и решим систему уравнений:

Полагая, что
![]() , имеем:
, имеем:
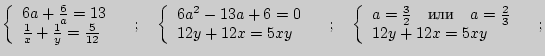
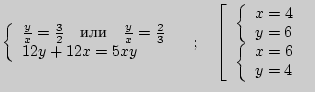
Ответ: 4 часа; 6 часов.
2. Задачи на движение
Задача 1. Пешеход прошел первую половину пути из пункта А в пункт В с постоянной скоростью, а с середины пути увеличил скорость на 1 км/ч и прошел вторую половину пути на 10 минут быстрее, чем первую. С какой скоростью шел пешеход вторую половину пути, если расстояние от А до В составляет 10 км?
Решение: Пусть ![]() км/ч - скорость пешехода на первой половине пути из А в В. Тогда
км/ч - скорость пешехода на первой половине пути из А в В. Тогда
![]() км/ч - скорость пешехода на второй половине пути. Время
движения пешехода на первой половине пути составляет
км/ч - скорость пешехода на второй половине пути. Время
движения пешехода на первой половине пути составляет
![]() часов, а
на второй
часов, а
на второй
![]() часов. Учитывая, что 10 минут - это
часов. Учитывая, что 10 минут - это
![]() часа, получаем уравнение:
часа, получаем уравнение:
![]() . После преобразований данное уравнение сводится к квадратному
уравнению
. После преобразований данное уравнение сводится к квадратному
уравнению
![]() , корни которого
, корни которого ![]() и
и ![]() . Так
как скорость движения - величина положительная, получаем
. Так
как скорость движения - величина положительная, получаем ![]() км/ч.
Значит, на второй половине пути скорость пешехода составляла 6 км/ч.
км/ч.
Значит, на второй половине пути скорость пешехода составляла 6 км/ч.
Ответ: 6 км/ч.
Задача 2. В 9 часов самоходная баржа вышла из пункта А вверх по реке и прибыла в пункт В. Спустя 2 часа после прибытия в пункт В эта баржа отправилась в обратный путь и прибыла в пункт А в 19 часов 20 минут того же дня. Учитывая, что скорость течения реки 3 км/ч, собственная скорость баржи все время постоянна и расстояние между пунктами А и В равно 60 км, определить, в котором часу баржа прибыла в пункт В.
Решение: Обозначим собственную скорость баржи через ![]() км/ч. Тогда время, затраченное
на движение по течению реки, составляет
км/ч. Тогда время, затраченное
на движение по течению реки, составляет
![]() часов, против
течения реки
часов, против
течения реки
![]() часов. Всего было затрачено времени:
часов. Всего было затрачено времени:
![]() часов. На основании этого составим
уравнение и решим его:
часов. На основании этого составим
уравнение и решим его:
![]() .
Его корни:
.
Его корни: ![]() и
и
![]() (не удовлетворяет условию).
(не удовлетворяет условию).
Так как время, затраченное на движение против течения реки, равно
![]() часов, то баржа прибыла в пункт В в 14 часов.
часов, то баржа прибыла в пункт В в 14 часов.
Ответ: в 14 часов.
3. Задачи на проценты
Задача 1. Первоначальная цена товара составляла 1000 рублей и была снижена сначала на 10 %, а затем еще на 20 %. Какова окончательная цена товара?
Решение: Первое снижение цены товара было на
![]() рублей. После
первого снижения цена товара составляла 1000 - 100 = 900 рублей. Второе
снижение цены товара было на
рублей. После
первого снижения цена товара составляла 1000 - 100 = 900 рублей. Второе
снижение цены товара было на
![]() рублей. После второго
снижения цена товара составляла 900 - 180 = 720 рублей.
рублей. После второго
снижения цена товара составляла 900 - 180 = 720 рублей.
Ответ: 720 рублей.
Задача 2. Сколько воды нужно добавить к 20 литрам пятипроцентного раствора соли, чтобы получить четырехпроцентный раствор?
Решение: Соль содержится в каждом из растворов. В 20 л пятипроцентного раствора
содержится
![]() (ед.) соли. Ее количество не меняется,
добавляется только вода. Выясним, каково ее количество.
(ед.) соли. Ее количество не меняется,
добавляется только вода. Выясним, каково ее количество.
Обозначим за ![]() (л) количество добавляемой воды. Из условия задачи получаем,
что четырехпроцентную концентрацию раствора характеризует уравнение
(л) количество добавляемой воды. Из условия задачи получаем,
что четырехпроцентную концентрацию раствора характеризует уравнение
![]() . Решив его, получим
. Решив его, получим ![]() = 5.
= 5.
Ответ: 5 л.
Задача 3. Из двух металлических брусков приготовили сплав, содержащий 15 % свинца. Известно, что первый брусок, состоявший из меди и свинца, весил 18 кг и содержал 80 % меди, а второй брусок весил 10 кг и состоял из свинца и олова. Найти процентное содержание олова во втором бруске.
Решение: Масса приготовленного сплава 18 + 10 = 28 кг. По условию, содержание в
сплаве свинца составляет
![]() кг. До переплавки в первом
бруске свинца было
кг. До переплавки в первом
бруске свинца было
![]() кг, из второго бруска в сплав попало
кг, из второго бруска в сплав попало
![]() кг свинца. Это количество составляет 6 % от массы
второго бруска. Значит, оставшиеся 94 % массы второго бруска составляло
олово.
кг свинца. Это количество составляет 6 % от массы
второго бруска. Значит, оставшиеся 94 % массы второго бруска составляло
олово.
Ответ: 94 %.
4. Задачи на зависимость между компонентами арифметических действий
Задача 1. Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найти исходное число.
Решение: Пусть ![]() - цифра десятков,
- цифра десятков, ![]() - цифра единиц,
- цифра единиц, ![]() - искомое двузначное
число. Из условия задачи следует:
- искомое двузначное
число. Из условия задачи следует:
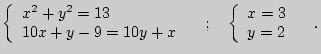 (х = -2 не подходит, так как х - цифра).
(х = -2 не подходит, так как х - цифра).
Следовательно, искомое число 32.
Ответ: 32.
Задача 2. Балкон имеет форму прямоугольника. С двух меньших сторон он покрыт одним
слоем утеплителя, а с третьей - двумя слоями. Площадь всего балкона 8
м![]() . После утепления балкон имеет размеры 3,6 м
. После утепления балкон имеет размеры 3,6 м ![]() 1,8 м. Какую
толщину имеет слой утеплителя? Выберите уравнение, соответствующее условию
задачи:
1,8 м. Какую
толщину имеет слой утеплителя? Выберите уравнение, соответствующее условию
задачи:
А.
![]() .
.
Б.
![]() .
.
В.
![]() .
.
Г.
![]() .
.
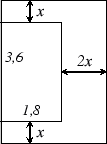
Решение: Если толщина утеплителя ![]() м, то длина балкона (прямоугольника) будет
м, то длина балкона (прямоугольника) будет ![]() , а его ширина
, а его ширина ![]() . Составим уравнение:
. Составим уравнение:
![]() .
.
Ответ: Г.