Элементы множества
Топологическим пространством ![]() называется
множество
называется
множество ![]() , в котором зафиксирован класс
, в котором зафиксирован класс ![]() подмножеств,
называемых открытыми, удовлетворяющий следующей системе
аксиом (аксиомы топологии для открытых подмножеств):
подмножеств,
называемых открытыми, удовлетворяющий следующей системе
аксиом (аксиомы топологии для открытых подмножеств):
![]()
![]() ;
;
![]()
![]() ;
;
![]() Для любого набора
Для любого набора
![]()
![]() , выполнено
, выполнено
![]()
![]() Для любого конечного набора
Для любого конечного набора
![]()
![]() , выполнено
, выполнено
![]()
Элементы множества ![]() называются точками, класс
называются точками, класс ![]() -
топологией на множестве
-
топологией на множестве ![]() .
.
Требование конечности в ![]() является существенным. В самом деле,
рассмотрим числовую прямую, класс открытых множеств которой
определен привычным из курса математического анализа способом.
Такая топология на числовой прямой называется классической.
Система вложенных интервалов
является существенным. В самом деле,
рассмотрим числовую прямую, класс открытых множеств которой
определен привычным из курса математического анализа способом.
Такая топология на числовой прямой называется классической.
Система вложенных интервалов
![]() обладает
единственной общей точкой
обладает
единственной общей точкой ![]() . Одноточечное множество на
числовой прямой не является открытым в классической топологии.
. Одноточечное множество на
числовой прямой не является открытым в классической топологии.
На одном и том же множестве могут быть введены различные
топологии. Например, считая открытыми на числовой прямой только
множества видов ![]() ,
, ![]() и
и
![]() ,
получим концентрическую топологию. Объявляя открытыми любые
объединения одноточечных подмножеств любого множества
,
получим концентрическую топологию. Объявляя открытыми любые
объединения одноточечных подмножеств любого множества ![]() , а также
пустое подмножество и само
, а также
пустое подмножество и само ![]() , получим дискретную
топологию, превращающую множество
, получим дискретную
топологию, превращающую множество ![]() в пространство
изолированных точек.
в пространство
изолированных точек.
Метрическим пространством называется множество ![]() ,
снабженное функцией
,
снабженное функцией
![]() ,
удовлетворяющей следующим аксиомам (аксиомы расстояния):
,
удовлетворяющей следующим аксиомам (аксиомы расстояния):
![]() Знакоопределенность:
Знакоопределенность:
![]() для любых точек
для любых точек
![]() и
и ![]() .
.
![]() Невырожденность:
Невырожденность: ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]()
![]() Симметричность:
Симметричность:
![]() для любых точек
для любых точек ![]() и
и ![]() .
.
![]() Неравенство треугольника:
Неравенство треугольника:
![]() для любых точек
для любых точек ![]() ,
, ![]() и
и ![]() .
.
Функция ![]() называется функцией расстояния, или метрикой.
называется функцией расстояния, или метрикой.
Метрическое пространство является топологическим. Индуцированная
метрикой ![]() топология на множестве
топология на множестве ![]() определяется следующим
образом: объявим открытыми подмножества
определяется следующим
образом: объявим открытыми подмножества
![]()
![]() и
всевозможные объединения подмножеств вида
и
всевозможные объединения подмножеств вида
![]() для всех положительных чисел
для всех положительных чисел ![]() и точек
и точек ![]() .
Выполнение аксиом
.
Выполнение аксиом ![]() -
- ![]() топологического пространства
нетрудно проверить самостоятельно.
топологического пространства
нетрудно проверить самостоятельно.
Далеко не всякое топологическое пространство допускает метрику, такую, чтобы топология была индуцирована этой метрикой.
Пусть
![]() - точка топологического пространства
- точка топологического пространства ![]() . Окрестностью точки
. Окрестностью точки ![]() называется любое открытое в
называется любое открытое в
![]() подмножество, содержащее точку
подмножество, содержащее точку ![]() .
.
Топологическое пространство ![]() называется хаусдорфовым, если для любых двух его различных точек
называется хаусдорфовым, если для любых двух его различных точек ![]() и
и ![]() найдутся непересекающиеся открытые окрестности, то есть множества
найдутся непересекающиеся открытые окрестности, то есть множества
![]() и
и
![]() , такие, что
, такие, что
![]() .
.
Хаусдорфовыми являются, например, числовая прямая с классической топологией, любое метрическое пространство с топологией, индуцированной метрикой, а также любое пространство изолированных точек. Числовая прямая с концентрической топологией нехаусдорфова.
Базой топологии пространства ![]() называется подкласс
называется подкласс
![]() такой, что для всякого открытого
подмножества
такой, что для всякого открытого
подмножества ![]() и для всякой точки
и для всякой точки ![]() найдется
такое подмножество
найдется
такое подмножество
![]() , что
, что
![]() .
.
Если пространство ![]() таково, что подкласс
таково, что подкласс ![]() может
состоять из счетного набора подмножеств, то говорят, что
может
состоять из счетного набора подмножеств, то говорят, что ![]() - пространство со счетной базой.
- пространство со счетной базой.
Пример топологического пространства со счетной базой легко построить. Таковым является числовая прямая с классической топологией. База топологии представлена интервалами с концами в рациональных точках. Множество таких интервалов, как нетрудно видеть, счетно. Читателю предлагается построить счетную базу классической топологии на плоскости.
Непрерывным называется отображение
![]() топологических пространств, при котором выполнено
следующее свойство: прообраз
топологических пространств, при котором выполнено
следующее свойство: прообраз ![]() каждого открытого в
пространстве
каждого открытого в
пространстве ![]() подмножества
подмножества
![]() открыт в пространстве
открыт в пространстве
![]() .
.
Отображение
![]() топологических
пространств называется гомеоморфизмом, если оно
топологических
пространств называется гомеоморфизмом, если оно
1) непрерывно,
2) взаимно однозначно,
3) обладает непрерывным двусторонним обратным отображением
![]() .
.
Нетрудно заметить, что для любого пространства ![]() постоянное отображение
постоянное отображение
![]() , где
, где
![]() - одноточечное пространство, непрерывно. При этом для любого
неодноточечного пространства
- одноточечное пространство, непрерывно. При этом для любого
неодноточечного пространства ![]() отображение
отображение ![]() не
является гомеоморфизмом (оно не взаимно однозначно и тем более не
обратимо).
не
является гомеоморфизмом (оно не взаимно однозначно и тем более не
обратимо).
Отношение гомеоморфности в классе топологических пространств рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности (докажите!)
Отображение ![]() топологических пространств называется локальным гомеоморфизмом, если у каждой точки
топологических пространств называется локальным гомеоморфизмом, если у каждой точки ![]() пространства
пространства
![]() имеется такая окрестность
имеется такая окрестность ![]() , что ограничение
, что ограничение
![]() отображения
отображения ![]() осуществляет гомеоморфизм окрестности
осуществляет гомеоморфизм окрестности ![]() на ее образ
на ее образ
![]() . При этом пространства
. При этом пространства ![]() и
и ![]() называются локально гомеоморфными.
называются локально гомеоморфными.
(Вещественным) топологическим многообразием (без края)
называется хаусдорфово топологическое пространство ![]() со
счетной базой, каждая точка которого обладает окрестностью,
гомеоморфной евклидову пространству
со
счетной базой, каждая точка которого обладает окрестностью,
гомеоморфной евклидову пространству
![]() . Число
. Число ![]() называется размерностью топологического многообразия
называется размерностью топологического многообразия ![]() .
.
Простейшими примерами топологических многообразий являются
числовая прямая с классической топологией и евклидова плоскость.
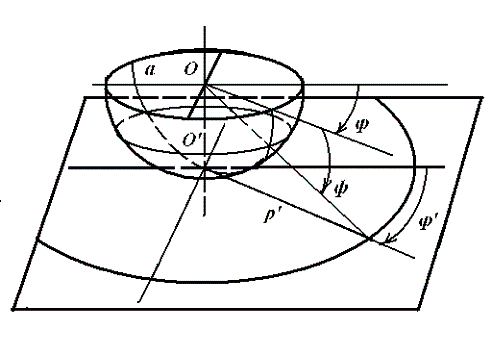
Более содержательный пример - двумерная сфера ![]() . В качестве
окрестности любой ее точки выберем содержащую эту точку открытую
полусферу (рис. 1). Гомеоморфизм открытой полусферы на касательную
плоскость, параллельную плоскости линии границы, определим с
помощью стереографической проекции. Выбрав сферические координаты
на полусфере радиуса
. В качестве
окрестности любой ее точки выберем содержащую эту точку открытую
полусферу (рис. 1). Гомеоморфизм открытой полусферы на касательную
плоскость, параллельную плоскости линии границы, определим с
помощью стереографической проекции. Выбрав сферические координаты
на полусфере радиуса ![]() и полярные координаты на плоскости так,
как показано на рис. 1
, получим:
и полярные координаты на плоскости так,
как показано на рис. 1
, получим:
![]()
![]() . Полученное
отображение непрерывно и взаимно однозначно. Обратное к нему
отображение задается формулами
. Полученное
отображение непрерывно и взаимно однозначно. Обратное к нему
отображение задается формулами
![]() ,
,
![]() . Оно непрерывно, так как непрерывны задающие его
функции.
. Оно непрерывно, так как непрерывны задающие его
функции.
(Вещественным) топологическим многообразием c краем
называется хаусдорфово топологическое пространство ![]() со счетной базой, каждая точка
которого принадлежит одному из двух следующих классов:
со счетной базой, каждая точка
которого принадлежит одному из двух следующих классов:
1) класс точек, каждая из которых обладает окрестностью,
гомеоморфной евклидову пространству
![]() ;
;
2) класс точек, каждая из которых обладает окрестностью,
гомеоморфной полупространству
![]() евклидова пространства
евклидова пространства
![]() .
.
Точки первого класса называются внутренними точками
многообразия ![]() , точки второго класса - точками границы
или точками края. Число
, точки второго класса - точками границы
или точками края. Число ![]() называется размерностью
топологического многообразия
называется размерностью
топологического многообразия ![]() .
.
Примерами одномерных многообразий с краем служат отрезок и полупрямая, примерами двумерных - круг и лента Мебиуса. Границы двух последних многообразий гомеоморфны окружности, в то время как сами многообразия негомеоморфны.
Для конструирования топологических многообразий часто используется
операция приклеивания, заключающаяся в следующем. Пусть ![]() и
и ![]() - топологические многообразия,
- топологические многообразия,
![]() ,
,
![]() - подмножества, причем
- подмножества, причем ![]() гомеоморфно
гомеоморфно ![]() . Пусть
. Пусть
![]() - гомеоморфизм. Отождествляя каждую точку
- гомеоморфизм. Отождествляя каждую точку ![]() с ее образом
с ее образом
![]() , получим новое многообразие
, получим новое многообразие
![]() , называемое склейкой многообразий
, называемое склейкой многообразий ![]() и
и ![]() вдоль гомеоморфизма
вдоль гомеоморфизма ![]() .
.
Для построения связной суммы многообразий ![]() и
и ![]() одинаковой размерности
одинаковой размерности ![]() выберем окрестности
выберем окрестности ![]() и
и ![]() точек
точек
![]() и
и ![]() соответственно, гомеоморфные открытому
соответственно, гомеоморфные открытому
![]() -мерному шару. Очевидно, границы многообразий
-мерному шару. Очевидно, границы многообразий
![]() и
и
![]() гомеоморфны (
гомеоморфны (![]() -мерной сфере). Пусть
-мерной сфере). Пусть ![]() -
какой-нибудь гомеоморфизм границ. Тогда связная сумма
-
какой-нибудь гомеоморфизм границ. Тогда связная сумма ![]() многообразий
многообразий ![]() и
и ![]() определяется как их склейка вдоль
гомеоморфизма
определяется как их склейка вдоль
гомеоморфизма ![]() (рис. 2).
(рис. 2).
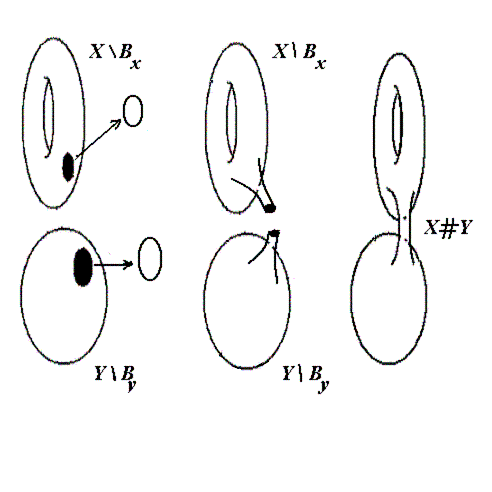
Евклидовым ![]() -мерным симплексом называется множество
-мерным симплексом называется множество
![]()
![]() -Мерной гранью евклидова симплекса
-Мерной гранью евклидова симплекса ![]() называется
евклидов симплекс
называется
евклидов симплекс
![]()
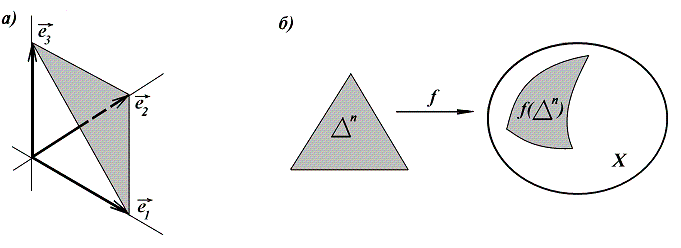
Топологическим ![]() -мерным симплексом в многообразии
-мерным симплексом в многообразии ![]() называется образ евклидова
называется образ евклидова ![]() -мерного симплекса при таком его
отображении
-мерного симплекса при таком его
отображении
![]() в многообразие
в многообразие ![]() , что
индуцированное им отображение
, что
индуцированное им отображение
![]() -
гомеоморфизм.
-
гомеоморфизм.
В дальнейшем мы не будем делать различия в обозначениях между топологическим симплексом и соответствующим ему евклидовым симплексом.
Различные топологические симплексы
![]() и
и
![]() назовем примыкающими правильно, если выполнено одно из условий:
назовем примыкающими правильно, если выполнено одно из условий:
1) симплексы не пересекаются;
2) симплексы имеют общую грань, являющуюся их пересечением;
3) один из симплексов является гранью другого.
Триангуляцией топологического многообразия ![]() называется
представление его в виде объединения некоторого набора симплексов,
причем различные симплексы примыкают правильно, и грань любого
симплекса не может быть инцидентна грани того же симплекса.
называется
представление его в виде объединения некоторого набора симплексов,
причем различные симплексы примыкают правильно, и грань любого
симплекса не может быть инцидентна грани того же симплекса.
Занумеруем вершины ![]() -мерного симплекса
-мерного симплекса ![]() по правилу:
вершина с номером
по правилу:
вершина с номером ![]() имеет координаты
имеет координаты
![]() (координата с номером
(координата с номером ![]() равна 1) и зафиксируем направление
обхода, то есть порядок перечисления его вершин, задаваемый
подстановкой
равна 1) и зафиксируем направление
обхода, то есть порядок перечисления его вершин, задаваемый
подстановкой
![]() (рис. 4). Два направления обхода
(рис. 4). Два направления обхода
![]() и
и
![]() одного симплекса
одного симплекса ![]() называются
равными, если задающие их подстановки имеют одинаковую четность, и
противоположными, если задающие их подстановки имеют различную
четность.
называются
равными, если задающие их подстановки имеют одинаковую четность, и
противоположными, если задающие их подстановки имеют различную
четность.
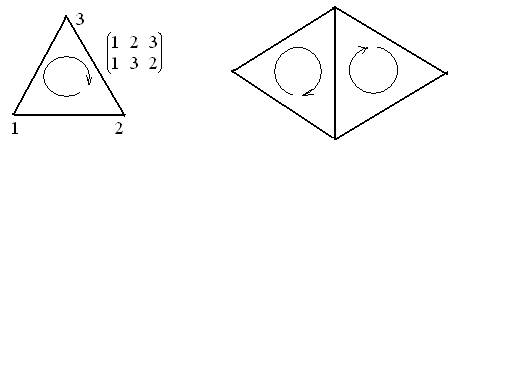
Ориентацией симплекса ![]() называется класс
равных направлений его обхода. Симплексы одинаковых размерностей
называется класс
равных направлений его обхода. Симплексы одинаковых размерностей
![]() и
и ![]() с общей гранью
с общей гранью
![]() согласованно ориентированы, если их ориентации на общей
грани противоположны (рис. 4).
согласованно ориентированы, если их ориентации на общей
грани противоположны (рис. 4).
Топологическое многообразие называется ориентируемым, если оно допускает триангуляцию, симплексы которой можно ориентировать согласованно, и неориентируемым в противном случае.
Можно показать, что ориентируемость (неориентируемость) многообразия не зависит от выбора его триангуляции.
Ориентируемыми многообразиями являются, например, евклидова плоскость, сфера и тор, неориентируемыми - лист Мебиуса, вещественная проективная плоскость и бутылка Клейна (см. задачи).
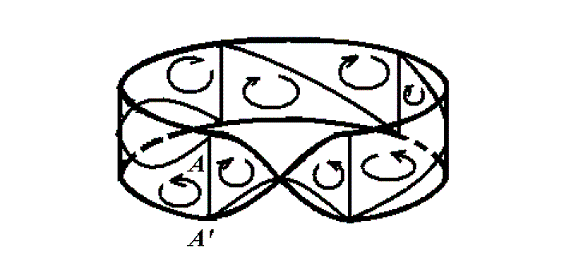
Покажем, что лента Мебиуса является неориентируемым многообразием.
Для этого выберем ее триангуляцию и ориентируем последовательно
каждый ее симплекс так, чтобы он был ориентирован соответственно
предыдущему (рис. 5). Тогда найдется ребро ![]() , на котором
индуцированы одинаковые ориентации.
, на котором
индуцированы одинаковые ориентации.
Ориентации двумерного симплекса на поверхности может быть поставлено в соответствие одно из двух возможных направлений нормали во внутренней точке симплекса. Это может быть сделано по известному из курсов аналитической геометрии и физики правилу буравчика. Направление нормали в точке поверхности указывает одну из двух сторон поверхности в окрестности этой точки. Если поверхность ориентируема, то задание ориентации фиксирует семейство направлений нормалей поверхности, причем направление нормали в точке не меняется при обходе любого замкнутого контура на поверхности, содержащего эту точку. Таким образом, гипотетический наблюдатель, совершающий путешествие по ориентируемой поверхности, всегда остается с одной ее стороны и не может попасть на другую. В этом смысле ориентируемые поверхности называют двусторонними. В случае неориентируемой поверхности ситуация обратная (рис. 6).
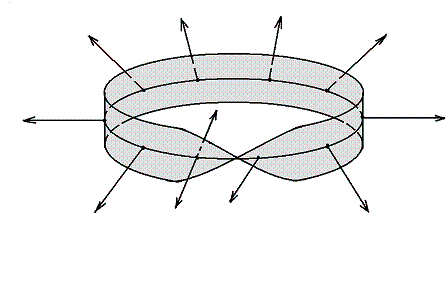
Существует замкнутый контур, при обходе которого направление нормали меняется на противоположное. При путешествии по такому контуру гипотетический наблюдатель, обойдя маршрут один раз, вернется в исходную точку, но окажется с другой стороны поверхности. Поэтому неориентируемые поверхности называют односторонними.
Ограничимся рассмотрением многообразий, допускающих триангуляцию из конечного числа симплексов.
Топологической эйлеровой характеристикой, или характеристикой Эйлера - Пуанкаре, данной триангуляции
многообразия ![]() называется число
называется число
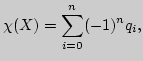
В подробных курсах топологии доказывается, что значение эйлеровой
характеристики зависит от многообразия ![]() , но не от выбора его
триангуляции. Также можно показать, что эйлеровы
характеристики гомеоморфных многообразий равны. Последнее
свойство означает неизменность эйлеровой характеристики при
гомеоморфизмах и называется топологической инвариантностью
эйлеровой характеристики.
, но не от выбора его
триангуляции. Также можно показать, что эйлеровы
характеристики гомеоморфных многообразий равны. Последнее
свойство означает неизменность эйлеровой характеристики при
гомеоморфизмах и называется топологической инвариантностью
эйлеровой характеристики.
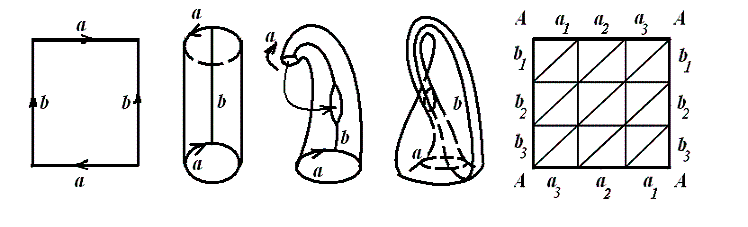
Вычислим эйлерову характеристику бутылки Клейна (рис. 7). Бутылка
Клейна может быть получена склейкой одной пары противоположных
сторон прямоугольника обычным образом, а другой пары сторон - с
обращением направления обхода, как показано на рисунке. Одна из
возможных триангуляций бутылки Клейна показана на рис. 7. Заметим,
что на схеме склейки одна и та же точка может иметь несколько
изображений. Например, вершина ![]() имеет четыре изображения, а
остальные точки сторон прямоугольника - по два изображения.
Также, некоторые грани триангуляции имеют по два изображения,
отождествляемые склейкой. Таковы грани
имеет четыре изображения, а
остальные точки сторон прямоугольника - по два изображения.
Также, некоторые грани триангуляции имеют по два изображения,
отождествляемые склейкой. Таковы грани ![]() ,
, ![]()
![]()
![]()
![]()
![]() . Остальные грани имеют по одному изображению.
Подсчитаем число граней, ребер и вершин триангуляции:
. Остальные грани имеют по одному изображению.
Подсчитаем число граней, ребер и вершин триангуляции: ![]()
![]()
![]() Таким образом, эйлерова характеристика бутылки
Клейна равна
Таким образом, эйлерова характеристика бутылки
Клейна равна
![]()
Топологическое многообразие ![]() называется дифференцируемым
называется дифференцируемым
класса ![]() (или
(или
![]() ), если
гомеоморфизмы
), если
гомеоморфизмы
![]() подчинены следующему
условию:
подчинены следующему
условию:
для любых ![]() ограничения отображений
ограничения отображений ![]() и
и ![]() согласованы в следующем смысле: определено отображение
согласованы в следующем смысле: определено отображение
![]() , задаваемое функциями, имеющими непрерывные частные производные
порядка
, задаваемое функциями, имеющими непрерывные частные производные
порядка ![]() (соответственно, имеющими непрерывные частные
производные любого порядка), такое, что
(соответственно, имеющими непрерывные частные
производные любого порядка), такое, что
![]() .
.
Отображения ![]() называются координатными отображениями,
пара
называются координатными отображениями,
пара
![]() - картой, а соответствующий покрытию
- картой, а соответствующий покрытию
![]() набор
набор
![]() - атласом
дифференцируемого многообразия
- атласом
дифференцируемого многообразия ![]() . Отображения
. Отображения
![]() иногда называют отображениями склейки.
иногда называют отображениями склейки.
Нетрудно убедиться в том, что отображения склейки обладают
следующими свойствами:
1) для любых ![]() справедливо свойство композиции:
справедливо свойство композиции:
![]() ;
;
2) для любых ![]() справедливо свойство коцикла:
справедливо свойство коцикла:
![]() , где символом
, где символом
![]() обозначено тождественное отображение евклидова
пространства.
обозначено тождественное отображение евклидова
пространства.
Многообразия класса
![]() называют также аналитическими.
называют также аналитическими.
Очевидно, что построенная нами структура вещественного
многообразия на двумерной сфере является, согласно только что
данному определению, структурой аналитического многообразия.
Задачи
1. Убедитесь в том, что, наряду с аксиомами
топологии для открытых множеств, топологическая структура на
множестве ![]() может быть задана следующей системой аксиом (аксиомы
топологии для
замкнутых множеств):
может быть задана следующей системой аксиом (аксиомы
топологии для
замкнутых множеств):
![]()
![]() замкнуто;
замкнуто;
![]()
![]() замкнуто;
замкнуто;
![]() Если
Если
![]() - произвольный набор замкнутых
множеств,
то множество
- произвольный набор замкнутых
множеств,
то множество
![]() замкнуто.
замкнуто.
![]() Если
Если
![]() - конечный набор замкнутых
множеств, то множество
- конечный набор замкнутых
множеств, то множество
![]() замкнуто.
замкнуто.
Указание. Определите открытое подмножество как дополнение к
замкнутому, а затем - замкнутое подмножество как дополнение к
открытому.
Приведите пример, показывающий, что требование
конечности в ![]() существенно.
существенно.
Указание. Постройте покрытие открытого интервала числовой
прямой (например, интервала ![]() ) отрезками.
) отрезками.
2. Докажите, что следующие топологические пространства
гомеоморфны (там, где это возможно, задайте отображение уравнениями и
докажите, что это отображение - гомеоморфизм. В других случаях
воспользуйтесь геометрическим построением и теоретико-множественным
определением):
1) окружность ![]() и треугольник
и треугольник ![]() ;
;
2) круг и плоский треугольник;
3) сфера ![]() и поверхность тетраэдра
и поверхность тетраэдра ![]() ;
;
4) поверхность куба и поверхность тетраэдра;
5) открытый интервал (0; 1) и открытый интервал (0; 10);
6) два произвольных открытых интервала;
7) открытый интервал и прямая;
8) открытый круг и плоскость;
9) открытое кольцо и плоскость без точки (проколотая плоскость).
3. Докажите, что данные преобразования евклидова пространства
являются гомеоморфизмами:
1) параллельный перенос на вектор ![]() ;
;
2) сжатие в направлении вектора ![]() c коэффициентом
c коэффициентом
![]() ;
;
3) поворот относительно начала координат на угол ![]() ;
;
4) линейное преобразование, заданное невырожденной матрицей ![]() .
.
4. Докажите, что открытый ![]() -мерный шар гомеоморфен
-мерный шар гомеоморфен ![]() -мерному
евклидову пространству. Укажите функциональное представление
отображения, осуществляющего гомеоморфизм. Сформулируйте новое
определение топологического многообразия с использованием открытых
шаров, и проверьте его эквивалентность известному Вам определению.
Можно ли его переформулировать в терминах локального
гомеоморфизма?
-мерному
евклидову пространству. Укажите функциональное представление
отображения, осуществляющего гомеоморфизм. Сформулируйте новое
определение топологического многообразия с использованием открытых
шаров, и проверьте его эквивалентность известному Вам определению.
Можно ли его переформулировать в терминах локального
гомеоморфизма?
5. Докажите, что данные подпространства евклидова пространства
можно снабдить структурой топологического многообразия:
1) параболоид вращения
![]() ;
;
2) эллипсоид
![]() ;
;
3) проективная плоскость как пространство классов векторов
трехмерного векторного пространства по отношению коллинеарности.
6. Укажите какую-нибудь триангуляцию данного топологического
многообразия. Вычислите эйлерову характеристику, используя эту
триангуляцию:
1) поверхность треугольной пирамиды;
2) поверхность четырехугольной пирамиды;
3) поверхность треугольной призмы;
4) треугольная призма;
5) поверхность куба;
6) поверхность икосаэдра;
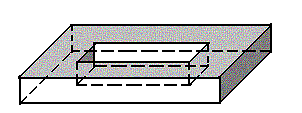
7) поверхность фигуры, изображенной на рис. 8 а) ("кольцо"
квадратного сечения).

7. Постройте две различные триангуляции данного топологического
многообразия и вычислите эйлерову характеристику, используя каждую
из них. Сравните результаты:
1) сфера;
2) шар;
3) тор (рис. 8 б));
4) полноторие (область пространства, ограниченная
тором);
5) лента Мебиуса.
8. Вычислите эйлеровы характеристики следующих топологических
многообразий:
1) вещественная проективная плоскость (рис. 9);
2) связная сумма тора и сферы;
3) тор рода 2 (связная сумма двух
торов);
4) связная сумма тора и бутылки Клейна.
9. Используя эйлерову характеристику, докажите, что данные
топологические многообразия не гомеоморфны:
1) сфера и проективная плоскость;
2) открытый диск и лента Мебиуса;
3) бутылка Клейна и тор рода 3.
10. Выясните, ориентируемы ли данные многообразия:
1) двумерная сфера;
2) круговой цилиндр;
3) тор;
4) тор рода 2;
5) бутылка Клейна;
6) вещественная проективная плоскость;
7) связная сумма тора и вещественной проективной плоскости. Ответ
обоснуйте, используя триангуляции многообразий.
11. Докажите, что данные подмножества евклидова пространства можно
снабдить структурой дифференцируемого многообразия. Сделайте
это и укажите порядок гладкости построенной Вами структуры:
1) плоскость ![]() ;
;
2) гиперболический параболоид
![]() ;
;
3) сфера (постройте какую-нибудь структуру дифференцируемого
многообразия, отличную от приведенной в примере);
4) тор.