Вопросы теории
Вторая квадратичная форма поверхности. Кривизна регулярной кривой
на поверхности. Теорема Менье. Нормальная кривизна поверхности в
данном направлении. Соприкасающийся параболоид и типы точек на
поверхности. Главные кривизны и главные направления поверхности в
точке. Полная (гауссова) и средняя кривизны поверхности.
Поверхности положительной, нулевой и отрицательной гауссовой
кривизны. Поверхности постоянной (положительной и отрицательной)
гауссовой кривизны. Деривационные формулы и символы Кристоффеля
для поверхности. Основные уравнения теории поверхностей. Теорема
Бонне. Геодезическая кривизна кривой на поверхности. Геодезические
линии на поверхности. Свойства геодезических. Примеры
геодезических линий на поверхностях. Существование и
единственность геодезической, проходящей через данную точку
поверхности в данном направлении. Реализации геодезических в
задачах физики. Понятие внутренней геометрии поверхности.
Геодезические линии и гауссова кривизна как объекты внутренней
геометрии. Теорема Гаусса - Бонне. Дефект геодезического
треугольника и топологическая инвариантность интегральной
кривизны.
Основные определения, результаты, комментарии
Второй квадратичной формой поверхности называется выражение
Подстановка в (7) с учетом того, что
![]() ,
приводит к равенству
,
приводит к равенству
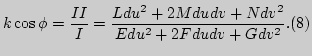
Далее будет введено "квадратичное приближение" формы поверхности в окрестности точки - так называемый соприкасающийся параболоид. В каждом конкретном случае он может оказаться гиперболическим или эллиптическим параболоидом, а также не исключено его вырождение в параболический цилиндр или плоскость.
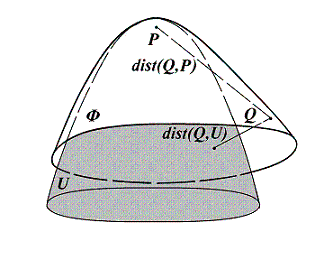
Пусть ![]() - дважды непрерывно дифференцируемая поверхность,
- дважды непрерывно дифференцируемая поверхность,
![]() - различные точки на поверхности
- различные точки на поверхности ![]() (рис. 27), и
(рис. 27), и ![]() -
параболоид, касающийся поверхности
-
параболоид, касающийся поверхности ![]() в точке
в точке ![]() .
.
Параболоид
![]() называется соприкасающимся параболоидом поверхности в ее
точке
называется соприкасающимся параболоидом поверхности в ее
точке ![]() , если выполнено соотношение
, если выполнено соотношение
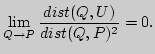
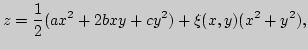
Первые и вторые производные координат в фиксированной точке одинаковы у поверхности и ее соприкасающегося параболоида в этой точке. Поэтому соприкасающийся параболоид имеет те же геометрические характеристики, что и исходная поверхность в данной точке, если эти характеристики выражаются через коэффициенты первой и второй квадратичных форм. Поворотом осей координат можно привести уравнение соприкасающегося параболоида к виду
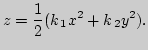
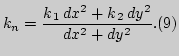
Линия на поверхности, направление которой в каждой точке является
главным, называется линией кривизны. Условие экстремума
нормальной кривизны в направлении ![]() может быть приведено к
виду (обратите внимание на порядок следования дифференциалов!)
может быть приведено к
виду (обратите внимание на порядок следования дифференциалов!)
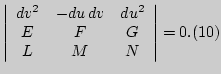
Во всех остальных случаях уравнение (10) имеет два корня- главных направления, которые дают дифференциальные уравнения линий кривизны. Можно доказать, что в окрестности любой точки, не являющейся омбилической точкой или точкой уплощения, поверхность может быть параметризована так, что координатные линии ее параметризации будут линиями кривизны.
Величины
![]() и
и
![]() называются соответственно
средней и гауссовой (полной) кривизнами
поверхности в точке. В случае произвольной параметризации средняя
и полная кривизны могут быть вычислены с использованием
коэффициентов первой и второй квадратичных форм:
называются соответственно
средней и гауссовой (полной) кривизнами
поверхности в точке. В случае произвольной параметризации средняя
и полная кривизны могут быть вычислены с использованием
коэффициентов первой и второй квадратичных форм:
Индикатриса кривизны, или индикатриса Дюпена, строится
в касательной плоскости в данной точке поверхности по следующему
правилу. Координатные оси в касательной плоскости совмещают с
главными направлениями. На луче, расположенном в каждом
направлении, откладывают отрезок, равный величине, обратной
квадратному корню из нормальной кривизны поверхности в этом
направлении, то есть
![]() .
.
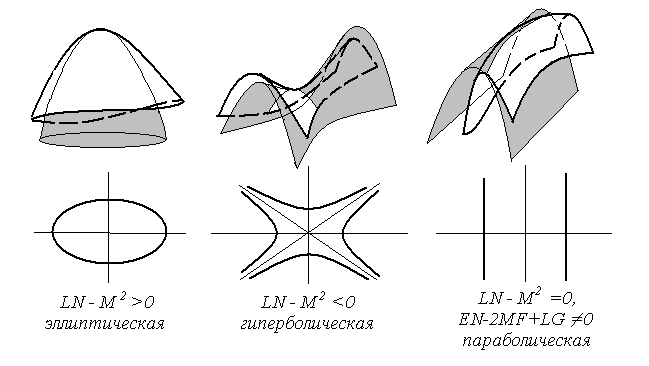
Кроме специального случая точки уплощения, различают типы точек на поверхностях, показанные на рис. 28. Существуют поверхности, состоящие из точек одного, двух или трех типов.
Направление ![]() на регулярной поверхности называется асимптотическим, если нормальная кривизна кривой этого
направления равна нулю. Линия на поверхности называется асимптотической, если в каждой точке ее касательная имеет
асимптотическое направление.
на регулярной поверхности называется асимптотическим, если нормальная кривизна кривой этого
направления равна нулю. Линия на поверхности называется асимптотической, если в каждой точке ее касательная имеет
асимптотическое направление.
Из теоремы Менье и уравнения (8) следует, что дифференциальное уравнение асимптотических линий имеет вид
Рассмотрим на ![]() -регулярной поверхности
-регулярной поверхности ![]() кривую
кривую
![]() класса
класса ![]() . Пусть
. Пусть ![]() - единичный вектор
касательной к этой кривой в точке
- единичный вектор
касательной к этой кривой в точке ![]() ,
, ![]() - единичный
вектор нормали поверхности
- единичный
вектор нормали поверхности ![]() в точке
в точке ![]() ,
, ![]() -
вектор кривизны кривой
-
вектор кривизны кривой ![]() в точке
в точке ![]() ,
, ![]() - естественный
параметр кривой. Вводя вектор
- естественный
параметр кривой. Вводя вектор
![]() ,
получим правый ортонормированный базис
,
получим правый ортонормированный базис
![]() . Разлагая в этом базисе вектор кривизны
. Разлагая в этом базисе вектор кривизны ![]() , имеем
, имеем
![]() где
где
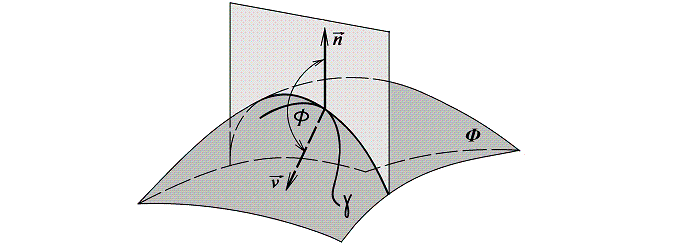
![]() Таким образом, нормальная кривизна поверхности
Таким образом, нормальная кривизна поверхности
![]() в направлении кривой
в направлении кривой ![]() есть проекция вектора
кривизны этой кривой на направление вектора нормали поверхности.
Коэффициент
есть проекция вектора
кривизны этой кривой на направление вектора нормали поверхности.
Коэффициент
![]() называется геодезической кривизной
называется геодезической кривизной ![]() кривой
кривой
![]() в точке
в точке ![]() Геодезическая кривизна кривой на поверхности
может быть вычислена в естественной параметризации по формуле
Геодезическая кривизна кривой на поверхности
может быть вычислена в естественной параметризации по формуле
![]()
Геодезической линией, или просто геодезической, называется линия, геодезическая кривизна которой в каждой ее точке равна нулю.
Иными словами, геодезическая - это кривая, направление которой в каждой ее точке совпадает с направлением нормального сечения поверхности.
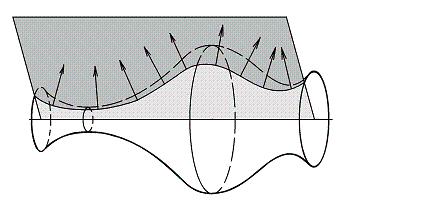
Например, известно, что нормаль поверхности вращения
принадлежит
плоскости, содержащей ось вращения. Поэтому
нормальные сечения поверхности вращения плоскостями, проходящими
через ее ось, являются геодезическими (рис. 29).
Можно доказать, что через каждую точку ![]() -регулярной
поверхности можно провести геодезическую линию, и притом
единственную. Замечательным свойством геодезической является также
то, что если точки
-регулярной
поверхности можно провести геодезическую линию, и притом
единственную. Замечательным свойством геодезической является также
то, что если точки ![]() и
и ![]() геодезической линии достаточно
близки, то дуга этой линии является кратчайшей среди всех дуг
кривых на данной поверхности, соединяющих точки
геодезической линии достаточно
близки, то дуга этой линии является кратчайшей среди всех дуг
кривых на данной поверхности, соединяющих точки ![]() и
и ![]() .
.
Аналогом формул Френе кривой являются деривационные
формулы
поверхности:
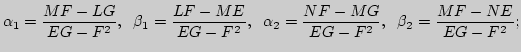
Если поверхность и ее параметризация являются
![]() -регулярными, то имеют место следующие уравнения связи
между коэффициентами первой и второй квадратичных форм
поверхности, называемые основными уравнениями теории
поверхностей. Это уравнения Петерсона - Кодацци:
-регулярными, то имеют место следующие уравнения связи
между коэффициентами первой и второй квадратичных форм
поверхности, называемые основными уравнениями теории
поверхностей. Это уравнения Петерсона - Кодацци:
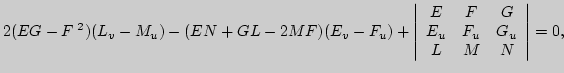
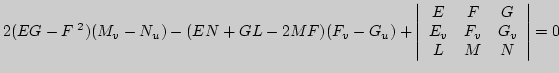
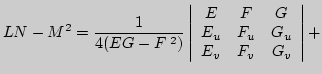
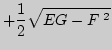 [(
[(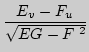 )
)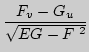 )
)
Оказывается, других связей между первой и второй квадратичными
формами нет, как утверждает теорема Бонне: если в открытой
области ![]() на плоскости переменных
на плоскости переменных ![]() заданы две квадратичные
формы, из которых первая положительно определена и ее коэффициенты
принадлежат классу
заданы две квадратичные
формы, из которых первая положительно определена и ее коэффициенты
принадлежат классу ![]() , а коэффициенты второй формы
принадлежат классу
, а коэффициенты второй формы
принадлежат классу ![]() , и притом коэффициенты заданных форм
удовлетворяют уравнениям Петерсона - Кодацци и Гаусса, то каждая
точка
, и притом коэффициенты заданных форм
удовлетворяют уравнениям Петерсона - Кодацци и Гаусса, то каждая
точка
![]() обладает окрестностью
обладает окрестностью
![]() ,
такой, что определено вложение
,
такой, что определено вложение
![]() ,
задающее поверхность класса
,
задающее поверхность класса ![]() , для которой данные
квадратичные формы являются соответственно первой и второй
квадратичным формами. Эта поверхность единственна с точностью до
перемещения.
, для которой данные
квадратичные формы являются соответственно первой и второй
квадратичным формами. Эта поверхность единственна с точностью до
перемещения.
К внутренней геометрии поверхности относят те геометрические характеристики поверхности, понятия и результаты, которые определяются первой квадратичной формой. Объектами внутренней геометрии являются длины кривых, площади областей, углы между кривыми на поверхности, а также геодезическая кривизна кривой на поверхности, символы Кристоффеля и полная кривизна поверхности. Объекты внутренней геометрии остаются неизменными при изометриях.
Пусть ![]() --
-- ![]() -регулярная замкнутая кривая на
поверхности
-регулярная замкнутая кривая на
поверхности ![]() , ограничивающая область
, ограничивающая область ![]() , гомеоморфную
кругу. Тогда справедливо соотношение
, гомеоморфную
кругу. Тогда справедливо соотношение
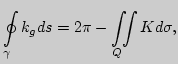
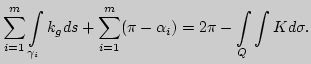
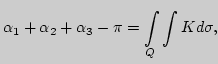
Пусть ![]() - замкнутая ориентируемая поверхность. Триангулируем
ее на геодезические треугольники
- замкнутая ориентируемая поверхность. Триангулируем
ее на геодезические треугольники
![]() . Тогда для каждого
из этих треугольников имеем
. Тогда для каждого
из этих треугольников имеем
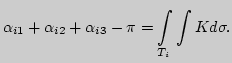
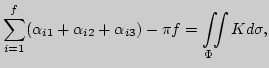
Задачи
1. Для каждой из данных поверхностей вычислите вторую квадратичную
форму, найдите гауссову и среднюю кривизны, а также главные
направления и главные кривизны этой поверхности в начале
координат:
а)
![]() ; в)
; в) ![]() ;
;
б)
![]() ; г)
; г) ![]() .
.
2. Найдите главные кривизны поверхности:
а) ![]() в точке (1,1,1);
в точке (1,1,1);
б)
![]() в точке (0,0,0).
в точке (0,0,0).
3. Вычислите вторую квадратичную форму:
а) сферы
![]()
б) поверхности вращения
![]()
в) кругового цилиндра
![]() ;
;
г) винтовой поверхности
![]() .
Проведите классификацию точек указанных поверхностей. Напишите
дифференциальные уравнения асимптотических линий. Там, где это
возможно, укажите явный вид асимптотических линий либо докажите,
что их нет.
.
Проведите классификацию точек указанных поверхностей. Напишите
дифференциальные уравнения асимптотических линий. Там, где это
возможно, укажите явный вид асимптотических линий либо докажите,
что их нет.
4. Дан эллипсоид
![]() . Найдите его вторую квадратичную форму, главные кривизны
в точках, расположенных на экваторе. Исследуйте характер точек
данной поверхности и проверьте, что координатная сеть является
сетью линий кривизны.
. Найдите его вторую квадратичную форму, главные кривизны
в точках, расположенных на экваторе. Исследуйте характер точек
данной поверхности и проверьте, что координатная сеть является
сетью линий кривизны.
5. Для данных поверхностей вычислите вторую квадратичную форму,
найдите среднюю кривизну и исследуйте характер точек:
а)
круговой цилиндр
![]() ;
;
б) прямой круговой конус
![]() .
Укажите линии кривизны произвольных цилиндрической и конической
поверхностей.
.
Укажите линии кривизны произвольных цилиндрической и конической
поверхностей.
6. Дана поверхность, образованная касательными к кривой
![]() , где
, где ![]() - естественный
параметр.
Вычислите вторую квадратичную форму поверхности, найдите гауссову и среднюю кривизны, а также главные
направления и главные кривизны этой поверхности.
- естественный
параметр.
Вычислите вторую квадратичную форму поверхности, найдите гауссову и среднюю кривизны, а также главные
направления и главные кривизны этой поверхности.
7. Дана поверхность переноса
![]() Найдите ее вторую квадратичную форму и вычислите полную кривизну.
Найдите ее вторую квадратичную форму и вычислите полную кривизну.
8. Дана псевдосфера
![]() . Вычислите полную и среднюю кривизны
псевдосферы. Проведите классификацию точек псевдосферы.
. Вычислите полную и среднюю кривизны
псевдосферы. Проведите классификацию точек псевдосферы.
9. Дан тор
![]() .
.
Вычислите его первую и вторую
квадратичные формы, площадь и проведите классификацию его точек.
Покажите на рисунке множества эллиптических, гиперболических и
параболических точек тора.
10. Найдите главные кривизны и главные направления прямого
геликоида
![]() докажите, что
главные направления делят пополам угол между винтовыми линиями и
прямолинейными образующими. Найдите линии кривизны винтовой
поверхности.
докажите, что
главные направления делят пополам угол между винтовыми линиями и
прямолинейными образующими. Найдите линии кривизны винтовой
поверхности.
11. Дана линейчатая поверхность, образованная главными нормалями
пространственной кривой
![]() где
где ![]() -
естественный параметр кривой
-
естественный параметр кривой ![]() . Найдите вторую квадратичную
форму данной поверхности и вычислите ее полную и среднюю кривизны.
. Найдите вторую квадратичную
форму данной поверхности и вычислите ее полную и среднюю кривизны.
12. Найдите линии кривизны поверхности вращения.
13. Докажите, что радиус геодезической кривизны (величина, обратная геодезической кривизне) параллели поверхности вращения равен отрезку касательной к меридиану, заключенному между точкой касания и осью поверхности.
14. Найдите геодезическую кривизну окружности радиуса ![]() на сфере
радиуса
на сфере
радиуса ![]() .
.
15. Докажите, что геодезические линии плоскости - прямые, геодезические линии сферы - окружности больших кругов. Можно ли доказать эти факты без использования формулы геодезической кривизны?