Далее: §3. Педагогический процесс наглядно-модельного Вверх: Теоретические основы наглядного моделирования Назад: §1. Дидактическая система математического

§2. Наглядность математических объектов

При изучении дидактических закономерностей в обучении математике одним из путей осуществления системного подхода является моделирование. Модель должна адекватно отражать основные, главные черты дидактической системы и должна быть описана математически; кроме того, необходимо учесть роль каждого определяющего структуру системного элемента, его функции и характеристики. Исходя из системного подхода, при исследовании наглядного обучения следует выявить структуру этого процесса, так как именно она и должна быть формализована при построении модели организации познавательной деятельности обучаемых. Изучение этой структуры невозможно без знания специфики учебного процесса и особенностей методики применения средств и видов наглядного обучения, без использования практического опыта имеющихся в педагогике подходов и методик. После изучения структуры наглядного обучения необходимо смоделировать систему организации и управления познавательной деятельности обучаемых в условиях целостного подхода и реализации гуманистических тенденций.

В этой связи исторический подход к наглядности в обучении математике как опоре на чувственное восприятие дает максимальный эффект в начальной школе и явно недостаточен при изучении высших разделов математики.

Здесь необходимо отметить три важных момента. Во-первых, настоящее исследование по проблеме наглядности в преподавании математики охватывает первое и необходимое звено познания - формирование представлений, возникающих на основе ощущений и восприятий. Представление, как правило, отражает лишь внешние признаки и стороны предметов и явлений материального мира, не всегда раскрывая их подлинную сущность, и именно наглядное моделирование позволит найти подходы к ее проявлению.

Процесс восприятия (особенно при больших объемах информации, большой степени его формализованности) предполагает наличие узловых, опорных, характерных, специфических свойств и качеств объекта восприятия, будь то приемы деятельности, отражающие отдельное математическое знание или организованный набор знаний (это может быть доказательство теорем, раздел курса математики во всем многообразии логических взаимосвязей, материал отдельного урока или лекции и т. п.).

Поэтому актуальной является проблема такой организации процесса обучения математике, когда представления, возникающие в мышлении обучаемых, отражают основные, существенные, ключевые стороны предметов и явлений, процессов, в том числе посредством разумного моделирования математического знания.

Именно формирование этих узловых, опорных качеств объекта восприятия (модель) и представляет собой суть процесса наглядного обучения. Такой подход a priori предполагает моделирование объекта восприятия с опорой на нейрофизиологические механизмы памяти и психологию восприятия. При этом особую значимость приобретают модели, фиксирующие процедуру математических действий. Рассмотрим следующий пример из высшей математики.

Пример. Пусть дано векторное поле $\vec A=(X,Y,Z),$ где $X=X(a,b,c),$
$Y=Y(a,b,c), Z=Z(a,b,c),\ \vec i, \vec j, \vec k$ - направляющие ортогональные единичные векторы. Ротор векторного поля $\vec A$ может быть определен следующим образом:

$${\rm rot}\vec A\buildrel{\rm def}\over= \vec i\left({\partia... ...\partial Y\over\partial a}-{\partial X\over\partial b}\right).$$

Это соотношение, как знаково-символическая форма, уже является моделью-заместителем реального явления. Однако процедура "появления" этого соотношения скрыта от обучаемых, понять, а значит, и лучше запомнить эту формулу непросто, тогда как, воспользовавшись понятием определителя третьего порядка и вектора градиента $\nabla=\left({\displaystyle\partial\over\displaystyle\partial x}, {\displaystyl... ...laystyle\partial y}, {\displaystyle\partial\over\displaystyle\partial z}\right)$ (устойчивые остаточные фреймы), ее легко воспроизвести:

$${\rm rot}\vec A=\left\vert \matrix{ \vec i&\vec j&\vec k\cr ... ...e\partial c}\cr \cr X&Y&Z\cr } \right\vert=\nabla\times\vec A,$$

как наглядную процедуру, связывающую понятие ротора с геометрическим понятием векторного произведения.

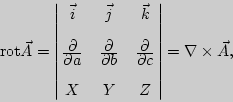
Во-вторых, процесс моделирования, поиск устойчивых ассоциаций, проверка адекватности восприятия предполагают серьезное проникновение в современные исследования нейрофизиологических механизмов восприятия, памяти и мышления, изучение этапов обработки стимула: сенсорного анализа, сличения с репертуаром памяти, принятия решения, использования законов и закономерностей психологии восприятия, целостного изучения динамической структуры личности обучаемых. Поэтому не менее актуальной является проблема дать психолого-педагогическое обоснование концепции наглядного обучения математике, расширить путем диагностических методик спектр психологических компонентов восприятия в процессе освоения учебной деятельности.

В-третьих, актуальность настоящего исследования определяется отсутствием единообразия трактовки принципа наглядности в обучении, слабым отражением специфики математической деятельности, оторванностью от практики, что не позволяет в полной мере использовать достижения психолого-педагогической науки. Деятельность учителя в процессе преподавания ввиду абстрактного характера, сложности и высокого уровня построения математического материала с необходимостью предполагает более детальную конкретизацию применяемых принципов обучения в направлении их системного использования. Таким образом, в настоящий период необходимо дать единую трактовку наглядного обучения и наглядности в обучении математике, разработать приемы деятельности учителя в процессе наглядного обучения, исследовать специфику наглядности в преподавании математики, используя положительный опыт передовых учителей и ученых.

Так как одной из задач педагогического процесса обучения математике является усвоение результатов знаково-символической деятельности, представленной в виде моделей, схем, кодов, знаков, символов, заместителей математических объектов, то большую роль приобретают:

- организация содержания и формы, структуры и объема знаково-символических средств, которая приводит к необходимости учета психологических закономерностей восприятия при их построении, возможностей и закономерностей нейрофизиологических механизмов памяти и мышления с целью усиления продуктивности восприятия (объем, точность, полнота, быстрота, эмоциональная окрашенность) и памяти (объем, точность запоминания и воспроизведения, прочность и точность запоминания);

- оперирование и организация познавательной деятельности со знаково-символическими средствами, объяснение с целью понимания и сознательного оперирования с математическими объектами.

При этом представление знаний в той или иной форме понимается как процесс, отражающий структуру, формы и методы описания, кодирования и моделирования знаний с целью управления, усвоения и принятия решения обучаемым, обеспечивающее их эффективное восприятие, интериоризацию, применение и дальнейшее преобразование.

Эти задачи ориентируют рассмотрение наглядности в целостном процессе обучения математике в тесной связи со знаково-символической деятельностью в направлении оптимального учета психологических и нейрофизиологических закономерностей восприятия, мышления и памяти.

Так как "наглядность есть особое свойство психических образов, создаваемых в процессах восприятия, памяти, мышления" [20], то проектируемая наглядность аккумулирует в себе учет наиболее известных и существенных закономерностей психофизиологических процессов познавательной деятельности обучаемого по овладению существом математических абстракций. В этом смысле в идеале проектируемая наглядность становится статистически универсальной для репрезентативной выборки обучаемых в процессе изучения математики, это позволяет, с одной стороны, приблизить наглядно-модельное обучение математике к уровню педагогической технологии, а с другой - возвращает свойство наглядности математическому объекту (в процессе наглядно-модельного обучения).

Рассмотрим следующий пример проявления сущности математического объекта наглядным моделированием. Понятие окрестности точки $z=z_0$ на расширенной комплексной плоскости ${\bf C}^*$ определяется в двух разновидностях: если
$z_0\in{\bf C}$, то

$$U(z_0)=\{z\in{\bf C}:\vert z-z_0\vert<\varepsilon \};$$

$z_0=\infty\in{\bf C}^*$, то

$$U(\infty)=\{z\in{\bf C}:\vert z\vert>R\}.$$

Обе знаково-символические формы воспринимаются обучаемым по отдельности неустойчиво как в перцептивном, так и в мнемических процессах, хотя и обладают наглядностью, в традиционном смысле присущей этим самым математическим объектам. Это подтверждается многолетними наблюдениями авторов и возможностью адекватного графического моделирования:

Рис. 14. Окрестности точки на комплексной плоскости

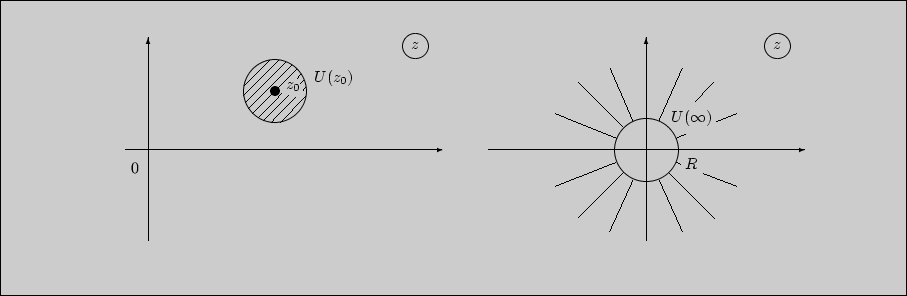
Однако само понятие окрестности точки в ${\bf C}^*$ как бы раздваивается, что не способствует адекватному восприятию этого математического объекта. Существуют как бы два различных определения окрестности, не связанные друг с другом. Постижение сути этого абстрактного понятия достигается через дополнительное моделирование, использующее стереографическую проекцию; сфера Римана, являясь моделью ${\bf C}^*$, дает возможность единой трактовки окрестности, в том числе и для $\infty$:

Рис. 15. Стереографическая проекция окрестности точки на сфере

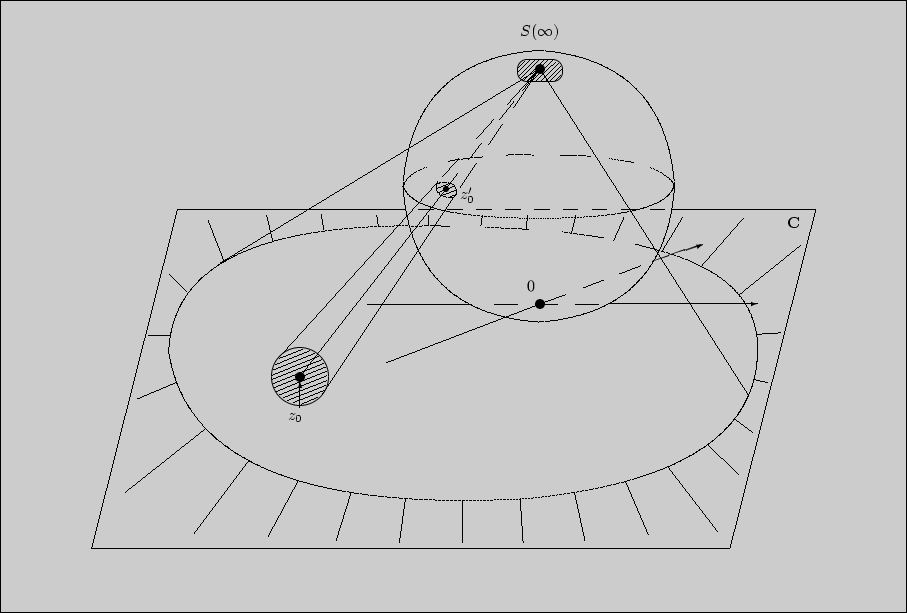
Но это свойство математического объекта (понятия окрестности точки на комплексной плоскости) активно формируется преподавателем в конкретных формах представления знания в проектировочной деятельности в рамках соответствующего целеполагания наглядно-модельного обучения и несет в себе черты методологической направленности, пусть даже неосознанной. Вряд ли классики комплексного анализа Б.Риман, О.Коши, Миттаг-Лефлер и др. понимали значимость проявления методологической сущности понятия окрестности в ${\bf C}$, но интуитивно блестяще "улавливали" эту наглядность в математическом объекте. Таких ярких методических находок в математике огромное множество, их только необходимо классифицировать, расширить их возможности для адекватного восприятия и сделать их появление закономерностью процесса, причем сам преподаватель может и должен стать творцом содержания наглядно-модельного обучения математике.

В процессе обучения математике наглядность математических объектов (или перцептивных образов) выполняет следующие функции:

- перцептивно-мнемическая, способствование лучшему восприятию и запоминанию, опора на нейро-физиологические закономерности восприятия, мышления и памяти, психофизиологические закономерности восприятия;

- семантическая, расширение знаково-символического опыта оперирования с математическими объектами (в том числе вербального);

- дидактическая, создание условий для когнитивной визуализации нового знания, проникновения в сущность понятий и теорем, квазиисследовательской деятельности студентов;

- развивающая, способствование развитию зрительной памяти, пространственного мышления, операций мышления (анализ, синтез, конкретизация, обобщение и т.п.), математических способностей;

- профессионально-педагогическая, обеспечивающая оптимальное дидактическое средство для проектирования будущей профессионально-математической деятельности в средней школе;

- стимулирующая, создание условий для поляризованного восприятия, устойчивого интереса, эмоционального и исторического фона, произвольного и непроизвольного внимания;

- эвристическая, создание ситуаций "интеллектуального затруднения" неполной информацией о формируемой модели, создание ситуаций на поиск ошибок [22], учебная деятельность на основе вариативности, самостоятельности и критичности;

- иллюстративная, способствующая оперативной адекватности восприятия математического знания, формированию системности знаний, созданию внешней опоры для внутренних действий обучаемых;

- воспитывающая, создание условий для познавательной и творческой активности, целостности восприятия математических объектов, взаимопереходов знаково-символических систем, формирования типологических свойств личности обучаемого.

Наглядность математического объекта может стать стимулом для пробуждения творческой активности студентов. Рассмотрим следующий пример. В математическом анализе кривых базовую роль играет понятие дифференциалов дуги: первого $ds$, второго $d^2s$ и т.д. Легко построить адекватную наглядную модель первого дифференциала $ds$, именно:

$$ds^2=dx^2+dy^2,$$

где $y=y(x)$ - непрерывно-дифференцируемая функция, $dx, dy$ - дифференциалы независимой и зависимой переменных соответственно. Тогда получим следующие иллюстрации:

Рис. 16. Геометрическая иллюстрация $ds$

$$dy=f'(x_0)dx=\vert MK\vert;\quad dx=\vert M_0L\vert;\quad ds=\vert M_0M\vert.$$

Или в вербальном выражении - геометрически первый дифференциал дуги в точке $x=x_0$ есть приращение касательной $l$ при переходе от $x_0$ к $x_0+dx$.

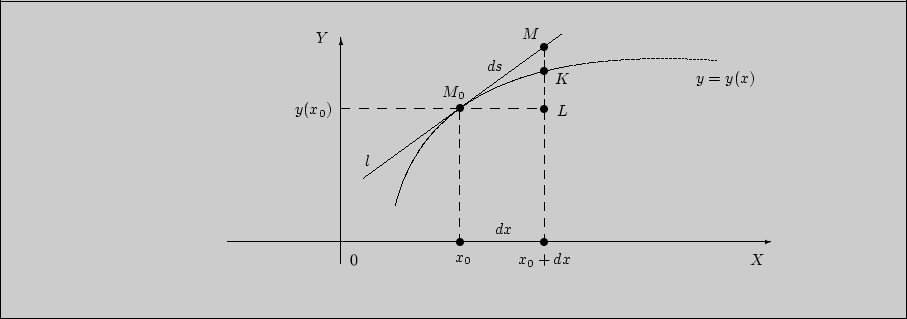
Но как только мы задумаемся об адекватной характеристике $d^2s$, то быстро выясняется, что кроме аналитического выражения геометрически (наглядно) $d^2s$ ни в одном учебном руководстве никто не выражал. Возникает довольно несложная математическая проблема, решение которой дает мощное средство устойчивости возникающего перцептивного образа (необходимо использовать не линейную, а квадратичную аппроксимацию в точке $x=x_0$). Педагогическая целесообразность таких находок очевидна.

Таким образом, наглядность - не только особое свойство психических образов, но и свойство математического объекта в рамках определенного дидактического процесса. Таковым он становится, когда у статистически достоверной выборки обучаемых возникают наглядные перцептивные образы (а значит, и у генеральной совокупности обучаемых). Это, возможно, снимает рассуждения такого свойства: "Поэтому можно говорить (и обычно так всегда и делают), что тот или иной предмет, явление, событие наглядны, имея в виду, что для нас наглядны образы этих объектов" [20].

Имеется в виду процесс наглядно-модельного обучения, когда наглядность математического объекта определяется соответствующими критериями.

Наглядность математического объекта (или перцептивного образа) определяется, как уже отмечалось, факторами восприятия, представления, мнемическими процессами в их единстве на основе диагностируемого целеполагания. Следующие критерии определяют существо наглядности математического объекта:

- диагностируемое целеполагание целостности математического объекта (моделирование, кодирование, схематизация, замещение);

- понимание обучаемым сущности математического объекта (адекватность восприятия);

- устойчивость перцептивного образа и представления;

- познавательная и творческая активность обучаемого на основе комфортности и успешности обучения.

Первый и третий критерий обуславливаются проектированием ООУД со знаково-символическими средствами дидактического процесса, второй и четвертый - знаково-символической деятельностью как обучаемого, так и обучающего (как внешнего, так и внутреннего плана). Более наглядно это представляется на следующей схеме:

Схема 6

Структура критериев наглядности перцептивного образа

Системная реализация в процессе обучения математике всех видов наглядности выступает фактом формирования целостных образов математических объектов, а значит, и значительно способствует усвоению математических знаний и развитию когнитивных способностей и математического мышления.

Далее: §3. Педагогический процесс наглядно-модельного Вверх: Теоретические основы наглядного моделирования Назад: §1. Дидактическая система математического