Общеучебные умения: владеть логическим анализом теоремы,
выделять условие, заключение теоремы, необходимое и достаточное
условие, формулировать обратную и противоположную теоремы;
силлогизмы, кванторы и пропозиционные связки, отрицание
высказываний, конструктивная теорема, теорема существования,
построение контрпримеров к условиям теоремы, построение
блок-схемы доказательства, структурный анализ учебных элементов.
Методы исследования и доказательства: "от противного",
метод Больцано, метод введения вспомогательной функции, метод
математической индукции, метод продолжения, метод математического
моделирования, метод последовательных приближений.
Историко-методическое оснащение: элементы историзма и
генезиса УЭ; отбор базовых и интегративных УЭ; взаимопереходы
знаковых систем; решение задач при ограничении условий (поиск
оптимальных условий); вариативность способов решения задач;
структурный анализ УЭ; единичное и особенное проявлений теорий
учения в моделировании процессов усвоения УЭ; актуализация фаз и
типов ориентировки и исполнения в учебной деятельности;
формирование культуры устной и письменной речи, мышления;
фундирование опыта и личностных характеристик в направлении
профессионализации; опора на устойчивые ассоциации, активизация
ментальных и личностных характеристик.
Знания: "наивное" и аксиоматическое построение теории
множеств, система обозначений. Конечные и бесконечные множества.
Задание множеств. Включение и равенство множеств. Булеан
множеств, число сочетаний ![]() Операции над множествами
(объединение, пересечение, разность, симметрическая разность,
декартово произведение).
Операции над множествами
(объединение, пересечение, разность, симметрическая разность,
декартово произведение).
Умения: приводить примеры конечных и бесконечных множеств,
производить операции над множествами, доказывать
теоретико-множественные равенства, использовать диаграммы
Эйлера-Венна.
Мотивация.
1. Понятие множества и элемента являются первичными в
математическом анализе. Теоретико-множественной базе принадлежит
главная роль в построении и организации математического анализа.
Одно из важнейших понятий, пронизывающих весь курс анализа, -
понятие числовой функции, определяется как специально заданное
соответствие между двумя числовыми множествами. Современная
теория множеств, созданная Георгом Кантором и его школой в конце
XIX в., глубоко проникла во многие области математики и оказала
на них огромное влияние.
2. Решите систему неравенств:
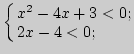 совокупность неравенств
совокупность неравенств
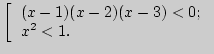 Как находится решение системы (совокупности) из множеств,
являющихся решениями соответственно первого и второго неравенств?
Как находится решение системы (совокупности) из множеств,
являющихся решениями соответственно первого и второго неравенств?
Теоретическая компонента
I. 1. Доказать, что каждое из условий: ![]()
![]()
![]()
![]() необходимо и достаточно для того, чтобы выполнялось включение
необходимо и достаточно для того, чтобы выполнялось включение
![]()
2. Привести примеры таких множеств ![]() и
и ![]() , что
, что
![]() В каком случае равенство выполняется?
В каком случае равенство выполняется?
II. 3. a) Доказать, что если ![]() , то
, то
![]()
б) Привести пример множеств ![]() таких, что
таких, что ![]() ,
но
,
но
![]() В каком случае выполняется равенство?
В каком случае выполняется равенство?
в) Доказать, что включение
![]() верно тогда и
только тогда, когда
верно тогда и
только тогда, когда
![]()
4. а) Привести пример таких множеств ![]()
![]()
![]()
![]() что
что
![]() но
но
![]()
б) Доказать, что если
![]() то
то
![]()
5. Доказать равенства:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
III. 6. Подсчитать число подмножеств конечного множества.
7. Дана система производных множеств ![]()
![]()
а) Пусть
![]() Доказать, что
Доказать, что
![]()
б) Пусть
![]() Доказать, что
Доказать, что
![]()
8. Пусть
![]() - система произвольных
множеств. Установить, верны ли включения:
- система произвольных
множеств. Установить, верны ли включения:
а)
![]() б)
б)
![]()
9. Даны множества ![]()
![]()
![]() С помощью операций
объединения и пересечения записать множество, состоящее из
элементов, принадлежащих
С помощью операций
объединения и пересечения записать множество, состоящее из
элементов, принадлежащих
а) всем трем множествам;
б) хотя бы одном множеству;
в) по крайней мере двум из этих множеств.
Практическая компонента
I. 1. Пусть
![]()
![]() Из каких элементов состоят множества:
Из каких элементов состоят множества:
а) ![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д) ![]() е)
е)
![]() ж)
ж) ![]() з)
з) ![]() ?
?
2. Пусть ![]()
![]()
![]() Найдите
множества а)
Найдите
множества а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
3. а) Выписать пять первых членов множества ![]() , где
, где
1)
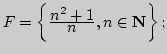 2)
2)
![]()
б) Из каких элементов состоят множества
![]()
![]() ?
?
4. Пусть множества ![]() и
и ![]() являются подмножествами множества
являются подмножествами множества
![]() , причем
, причем
![]() Изобразить на диаграмме
Эйлера-Венна следующие множества:
Изобразить на диаграмме
Эйлера-Венна следующие множества: ![]()
![]() ,
,
![]()
![]()
![]()
![]()
5. Пусть
![]()
![]()
![]() Найдите
Найдите ![]()
![]()
![]()
![]()
6. Пусть множество ![]() содержит
содержит ![]() элементов, множество
элементов, множество ![]() -
- ![]() элементов, а пересечение
элементов, а пересечение ![]() -
- ![]() элементов. Найти
число элементов множества а)
элементов. Найти
число элементов множества а) ![]() , б)
, б) ![]()
Деятельностная компонента
I. 1. Изобразить на плоскости множества ![]() и
и ![]() . Найти
. Найти
![]() ,
, ![]() , где
, где
а)
![]()
![]()
б)
![]()
![]()
II. 2. Множество ![]() задается неравенством
задается неравенством ![]() множество
множество ![]() - неравенством
- неравенством ![]() ; множество
; множество ![]() -
неравенством
-
неравенством ![]() множество
множество ![]() - неравенством
- неравенством ![]() Изобразить на плоскости следующие множества: а)
Изобразить на плоскости следующие множества: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Прикладная компонента
I. 1. Найдите
![]() и
и
![]() , если
, если ![]() заданы следующим
образом:
заданы следующим
образом:
а)
![]() б)
б)
![]() в)
в)
![]() д)
д)
![]() е)
е)
![]()
2. Для множеств из предыдущего примера найти
![]() и
и
![]() .
.
3. Найдите
![]() и
и
![]() ,
где
,
где
а) ![]() - множество всех треугольников, вписанных в данную
окружность (каждый треугольник рассматривается как часть
плоскости);
- множество всех треугольников, вписанных в данную
окружность (каждый треугольник рассматривается как часть
плоскости);
б) ![]() - множество всех правильных треугольников, вписанных в
данную окружность;
- множество всех правильных треугольников, вписанных в
данную окружность;
в) ![]() - множество всех остроугольных (прямоугольных,
тупоугольных) треугольников, вписанных в данную окружность.
- множество всех остроугольных (прямоугольных,
тупоугольных) треугольников, вписанных в данную окружность.
4. Проиллюстрируйте геометрически декартово произведение а) двух отрезков; б) двух прямых; в) прямой и окружности; г) прямой и круга; д) двух окружностей.
5. Множество
![]() называется
диагональю декартова квадрата
называется
диагональю декартова квадрата ![]() множества
множества ![]() .
Проиллюстрируйте геометрически диагонали множеств, получившихся в
пунктах а), б), д).
.
Проиллюстрируйте геометрически диагонали множеств, получившихся в
пунктах а), б), д).
Знания: аксиомы сложения, умножения, порядка, связи, аксиома непрерывности Дедекинда, теоремы существования разности и частного, основные следствия из аксиом.
Умения: доказывать теоремы существования разности ![]() и
частного
и
частного ![]() действительных чисел. Доказывать теорему
действительных чисел. Доказывать теорему
![]() и другие общие свойства
действительных чисел.
и другие общие свойства
действительных чисел.
Навыки. Навыки оперирования с действительными числами.
Методы. Метод математической индукции.
![\begin{picture}(77.00,15.00)
\put(45.00,10.00){\makebox(0,0)[cc]{${}^\cdot_/{\bf...
....00}{8}
\put(57.00,5.00){\dashbox{2.00}(20.00,8.00)[cc]{$n:=n+1$}}
\end{picture}](img729.png)
Мотивация. 1. Число - это важнейшее математическое понятие, развитие которого происходило на протяжении развития человеческой цивилизации и было обусловлено как практической деятельностью человека, так и явилось следствием развития математики.
XIX век ознаменовался критическим пересмотром основ классического математического анализа и прежде всего учения о числе. К тому времени был накоплен огромный фактический материал, но он являлся недостаточно разработанным в логическом отношении. Действительное число трактовалось на геометрической основе, при этом существенную роль играла геометрическая интуиция. Современная теория действительных чисел ведет свое начало от работ Гаусса, Больцано, Коши и окончательно оформилась в работах немецких математиков Дедекинда, Вейерштрасса и Кантора. Аксиомы действительных чисел были впервые сформулированы Дедекиндом в 1888 г. и итальянским математиком Пеано в 1891 г.
2. Как уже отмечалось, функции являются объектом изучения
математического анализа, в первую очередь вещественнозначные
функции одного переменного. Функции отображают одно множество
действительных чисел в другое, поэтому прежде чем изучать
функции, необходимо изучить множество ![]() .
.
3. Понятие числа изучается на протяжении всего школьного курса математики: "числа и вычисления" - одна из основных содержательных линий школьного курса. Будущий учитель должен владеть теорией действительного числа. Кроме того, студенты знакомятся с аксиоматическим способом определения понятия в анализе, а не только в геометрии.
Теоретическая компонента
I. 1. Доказать единственность единичного элемента и нуля
в ![]()
2. Доказать, что в ![]() у каждого элемента имеется
единственный противоположный элемент, и для
у каждого элемента имеется
единственный противоположный элемент, и для ![]() обратный к
нему элемент
обратный к
нему элемент ![]() - единственный.
- единственный.
3. Уравнения ![]() и
и ![]() в
в ![]() имеют
единственные решения.
имеют
единственные решения.
4. Для любого ![]() выполнено
выполнено ![]()
5.
![]()
6.
![]() имеет место одно из соотношений
имеет место одно из соотношений
![]()
7. Если ![]() , то
, то
![]()
![]()
II. 8. Докажите, что
а)
![]()
б)
![]()
в)
![]()
г) ![]()
д)
![]()
9. Докажите равенство ![]()
III. 10. Верны ли утверждения:
а)
![]()
б)
![]()
в)
![]()
11. Докажите, что
![]()
Метод математической индукции.
I. 1. Доказать, что для любого ![]() справедливы
равенства:
справедливы
равенства:
а)
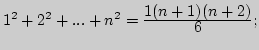
б)
![]()
в)
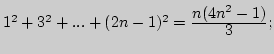
г)
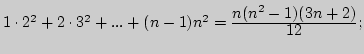
д)
![]()
е)
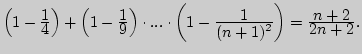
II. 2. Доказать неравенство:
![]() где
где
![]()
![]() ...
... ![]() - числа одного и того же знака, большие
- числа одного и того же знака, большие
![]() .
.
3. Доказать неравенство Бернулли:
![]()
![]()
![]()
4. Доказать формулу бинома Ньютона:
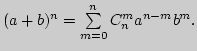
5. Доказать неравенство:
![]()
6. Доказать неравенство:
![]()
III. 7. Доказать, что при любом ![]() верно неравенство:
а)
верно неравенство:
а) ![]() б)
б)
![]() в)
в)
![]()
8. Доказать неравенство:
а)
![]() б)
б)
![]()
9. Найти сумму
![]()
10. Доказать равенство
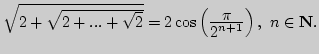
Знания: определение модуля действительного числа, свойства модуля. Модуль суммы, разности, произведения. Неравенство треугольника. Теорема Архимеда и следствия из нее.
Умения: доказывать свойства модуля, проводить аналитическое
и графическое доказательства неравенства треугольника. Доказывать
следствие теоремы Архимеда:
![\begin{picture}(68.00,15.00)
\put(52.00,10.00){\makebox(0,0)[cc]{$\bbuildrel{\ve...
...00}{15}{63.00}{5.00}{16}
\emline{63.00}{5.00}{17}{41.00}{5.00}{18}
\end{picture}](img777.png)
Мотивация.
1. Модули используются в определении
фундаментального понятия математического анализа - понятия
предела.
2. Теорема Архимеда и ее следствия имеют исключительно важное
значение. На их основе, в частности, доказывается возможность
представления любого натурального числа в позиционной ![]() -ичной
системе счисления.
-ичной
системе счисления.
3. Пусть ![]() и
и ![]() - две точки на числовой прямой. Как найти
расстояние между ними?
- две точки на числовой прямой. Как найти
расстояние между ними?
4. Какому неравенству удовлетворяют точки, удаленные от точки 2 на расстояние, большее, чем 4 (меньшее, чем 3)?
Теоретическая компонента
I. 1. Доказать, что для
![]() справедливы
соотношения:
справедливы
соотношения: ![]()
![]()
![]()
II. 2. Доказать, что для
![]() и
и
![]()
![]()
![]()
![]()
![]() Найдите необходимое и
достаточное условия, при котором неравенство будет равенством.
Найдите необходимое и
достаточное условия, при котором неравенство будет равенством.
3. Докажите:
![]()
4. Найти а)
![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() д)
д) ![]()
Практическая компонента
I. 1. Решить неравенства и уравнения с модулем:
а) ![]()
![]()
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
![]()
ж)
![]()
II. 2. Решить неравенства и уравнения с модулем:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
Знания: определение классов действительных чисел. Целая и дробная часть действительного числа, диофантовы уравнения. Наибольший общий делитель, наименьшее общее кратное двух натуральных чисел. Системы счисления. Позиционная запись натуральных чисел. Понятие бита и байта информации. Двоичная система счисления и ЭВМ.
Умения. Находить НОД, НОК двух натуральных чисел, решать
диофантовы уравнения ![]() с помощью алгоритма Евклида.
Представлять натуральные числа в различных системах счисления.
с помощью алгоритма Евклида.
Представлять натуральные числа в различных системах счисления.
Мотивация.
1. Натуральные числа, используемые для счета в практической
деятельности, появились на самых ранних этапах развития
человеческой цивилизации. Первоначально понятие числа
отсутствовало - число было привязано к пересчитываемым
предметам. Отвлеченное понятие натурального числа появляется и
закрепляется с развитием письменности и введением для обозначения
чисел определенных символов.
2. В чем отличие записи чисел в позиционной системе счисления от непозиционной? Какие вы знаете примеры позиционных и непозиционных систем счисления?
3. Представьте число 48501 в виде суммы степеней десяти.
![\begin{picture}(99.00,13.00)
\put(19.00,9.00){\makebox(0,0)[cc]{${\bf R}$}}
\eml...
...00}{29}{33.00}{13.00}{30}
\emline{33.00}{5.00}{31}{5.00}{5.00}{32}
\end{picture}](img811.png)
Теоретическая компонента
I. 1. Доказать, что если ![]()
![]()
![]() , то
существует и притом единственное представление числа
, то
существует и притом единственное представление числа ![]() в виде
в виде
2. Обозначим НОД чисел ![]() и
и ![]() через
через ![]() Доказать, что
если
Доказать, что
если ![]()
![]() то
то ![]()
3. Доказать, что совокупность общих делителей двух натуральных чисел совпадает с совокупностью делителей их наибольшего общего делителя.
Практическая компонента
I. 1. Найдите НОД (158;204). Найдите все решения
диофантова уравнения ![]()
![]()
2. Найдите с помощью алгоритма Евклида НОД (13172;261). Найдите НОК (49896;26460).
3. Постройте графики функций ![]()
![]()
![]()
![]()
![]()
![]()
4. Переведите следующие числа в 10-чную систему: ![]()
![]()
![]()
![]()
![]()
5. Переведите из 10-чной системы в ![]() -чную:
-чную:
![]()
![]()
![]()
![]()
6. Запишите ![]() в двоичной и троичной системах.
в двоичной и троичной системах.
II. 7. Напишите таблицу умножения и сложения для
шестеричной системы счисления. Используя их, вычислить в
шестеричной системе: а)
![]() б)
б) ![]() в)
в)
![]()
8. Разложить рациональную дробь на простейшие в ![]() :
а)
:
а)
![]()
б)
![]() в)
в)
![]()
9. Вычислить суммы: а)
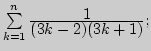 б)
б)
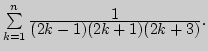
Знания: рациональные числа. Плотность рациональных чисел в
![]() . Алгебраические и трансцендентные числа. Теорема о
плотности
. Алгебраические и трансцендентные числа. Теорема о
плотности
![]() Числа
Числа ![]() и
и ![]() . Бином Ньютона и
неравенство Бернулли.
. Бином Ньютона и
неравенство Бернулли.
Умения: доказывать теорему о плотности ![]() в
в ![]() доказывать сепарабельность некоторых чисел, приводить 10 примеров
алгебраических и трансцендентных чисел.
доказывать сепарабельность некоторых чисел, приводить 10 примеров
алгебраических и трансцендентных чисел.
Навыки: оперирование с числами из ![]() в дробном
представлении
в дробном
представлении
![]() , нахождение десятичных
приближений с заданной точностью.
, нахождение десятичных
приближений с заданной точностью.
![\begin{picture}(32.00,11.00)
\put(16.00,8.00){\makebox(0,0)[cc]{10}}
\emline{5.0...
...}{8.00}{7}{27.00}{5.00}{8}
\emline{27.00}{5.00}{9}{5.00}{5.00}{10}
\end{picture}](img849.png)
Мотивация. 1. Потребность в измерении величин таких, как
длина, площадь, объем, привела к появлению рациональных чисел.
Положительные дроби были известны еще древним цивилизациям
Вавилона и Египта; как полагают, индийцы изобрели число нуль.
Отрицательные рациональные числа были введены в Италии в эпоху
Возрождения.
2. Существование иррациональных чисел было установлено еще в
Древней Греции, когда "несоизмеримость" диагонали квадрата с его
стороной обнаружила сложность и несовершенство представлений
об
окружающем мире. Осознание этого факта привлекло внимание ученых
к строгим математическим методам доказательства, а теория
пропорций Евдокса - одно из блестящих достижений
древнегреческой математики - заложила основы современной теории
действительных чисел.
3. Существование трансцендентных чисел было впервые установлено
французским математиком И.Лиувиллем в 1844 г. Однако впервые
конкретные примеры трансцендентных чисел появились лишь в конце
XIX в. Именно французский математик Ш.Эрмит в 1873 г. доказал
трансцендентность числа
![]() , а немецкий
математик Ф.Линдеман в 1882 г. установил трансцендентность числа
, а немецкий
математик Ф.Линдеман в 1882 г. установил трансцендентность числа
![]() чем доказал невозможность квадратуры круга - построить с
помощью циркуля и линейки квадрат, площадь которого равна площади
круга, - проблему, остававшуюся без ответа на протяжении
столетий.
чем доказал невозможность квадратуры круга - построить с
помощью циркуля и линейки квадрат, площадь которого равна площади
круга, - проблему, остававшуюся без ответа на протяжении
столетий.
4. Всегда ли сумма двух рациональных чисел есть число рациональное? А сумма рационального и иррационального?
5. Если высота треугольника имеет длину 5 см и делит основание
треугольника на отрезки длиной 2 и 5 см, то периметр треугольника
равен
![]() В практической деятельности для
сложения иррациональных чисел используют десятичные приближения.
В практической деятельности для
сложения иррациональных чисел используют десятичные приближения.
Теоретическая компонента
I. 1. Докажите или опровергните:
а) сумма рациональных чисел рациональна;
б) сумма иррациональных чисел иррациональна;
в) сумма рационального и иррационального числа иррациональна.
Проверьте аналогичные утверждения для разности, частного и произведения.
II. 2. Доказать, что если ![]() , то
, то ![]() -
либо натуральное, либо иррациональное число.
-
либо натуральное, либо иррациональное число.
3. Доказать эквивалентность утверждений:
а) между любыми двумя рациональными числами заключено хотя бы одно рациональное число;
б) между любыми двумя рациональными числами заключено бесконечно много рациональных чисел.
Верно ли это утверждение для иррациональных чисел?
III. 4. Доказать, что для любых рациональных чисел ![]() и
и
![]() таких, что
таких, что ![]() , найдется иррациональное число
, найдется иррациональное число ![]() ,
удовлетворяющее условию
,
удовлетворяющее условию ![]()
5. Доказать, что существует иррациональное число ![]() , для
которого неравенство
, для
которого неравенство
![]() имеет
бесконечное множество решений в целых числах
имеет
бесконечное множество решений в целых числах ![]() и
и ![]()
![]() .
.
Практическая компонента
I. 1. Доказать, что данные числа иррациональны:
а)
![]()
б)
![]() в)
в)
![]()
в)
![]()
II. 2. Докажите, что всякое число, в котором нули стоят
на всех местах с номерами ![]() и только на этих местах, является
иррациональным.
и только на этих местах, является
иррациональным.
3. Доказать, что для
![]() , из которых хотя бы
одно число не равно нулю, число
, из которых хотя бы
одно число не равно нулю, число
![]() - иррационально.
- иррационально.
4. Сумма и разность двух чисел ![]() и
и ![]() есть число
рациональное. Докажите, что
есть число
рациональное. Докажите, что ![]() и
и ![]() также являются
рациональными.
также являются
рациональными.
5. Пусть ![]() и
и ![]() - иррациональные числа, а
- иррациональные числа, а
![]() - рационально. Докажите, что числа
- рационально. Докажите, что числа ![]() и
и
![]() иррациональны.
иррациональны.
6. Числа ![]() ,
, ![]() и
и
![]() являются рациональными.
Доказать, что
являются рациональными.
Доказать, что ![]()
![]() ,
, ![]() ,
, ![]() - также рациональные числа.
- также рациональные числа.
Деятельностная компонента
I. 1. Записать рациональные числа в виде бесконечных
десятичных дробей:
2. Записать периодические бесконечные десятичные дроби в виде
обыкновенных дробей:
3. Найдите десятичные приближения чисел
![]()
![]() ,
,
![]() по недостатку и по избытку с
точностью до 0,1; 0,01; 0,001.
по недостатку и по избытку с
точностью до 0,1; 0,01; 0,001.
Знания: определение длины отрезка на прямой ![]() .
Соизмеримые отрезки. Построение отрезка, соизмеримого с данным.
Установление взаимнооднозначного соответствия между
.
Соизмеримые отрезки. Построение отрезка, соизмеримого с данным.
Установление взаимнооднозначного соответствия между ![]() и
точками
и
точками ![]() . Числовая прямая. Несобственные точки
. Числовая прямая. Несобственные точки ![]() и
и
![]() , оперирование с бесконечностями.
, оперирование с бесконечностями.
Практическая компонента
I. 1. Соизмеримы ли отрезки, если отношение их длин выражается дробью 0,23(75)?
Деятельностная компонента
I. 1. Дан отрезок ![]() . С помощью циркуля и линейки
постройте отрезок
. С помощью циркуля и линейки
постройте отрезок
![]()
![]()
![]()
![]()
Знания: классификация промежутков на числовой прямой. Система вложенных промежутков. Теорема Кантора.
Умения: доказывать теорему Кантора, владеть понятием
арифметической и геометрической прогрессии, находить сумму
бесконечного числа членов геометрической прогрессии.
Методы: метод Больцано (дихотомии).

Мотивация. 1. Найдите
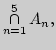 где
а)
где
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() Найдите в каждом случае
Найдите в каждом случае
![]()
2. Каким может быть пересечение конечной (бесконечной) системы вложенных отрезков (интервалов)?
Теоретическая компонента
II. 1. Справедливо ли утверждение: всякая система
вложенных интервалов ![]() , т.е. таких, что
, т.е. таких, что
![]()
![]() , имеет непустое
пересечение? Привести пример.
, имеет непустое
пересечение? Привести пример.
2. Привести пример системы вложенных интервалов, имеющих одну точку пересечения (содержащих в пересечении отрезок).
3. Привести пример последовательности вложенных отрезков
![]() такой, что
такой, что
![]() содержит не менее двух точек.
содержит не менее двух точек.
4. Отрезком ![]() рациональных чисел называется
множество
рациональных чисел называется
множество
![]()
Система
![]() отрезков
рациональных чисел называется вложенной, если для любого
отрезков
рациональных чисел называется вложенной, если для любого ![]() выполняется включение
выполняется включение
Знания: понятие окрестности точки на числовой прямой (собственной и несобственной). Отделимость окрестностей. Понятие предельной точки, внутренней точки. Понятие открытого множества, замкнутого множества.
Умения: доказывать теорему об отделимости окрестностей. Приводить 10 примеров: предельных точек, внутренних точек, открытых, замкнутых множеств.

Мотивация. 1. Понятие окрестности позволяет раскрыть
структуру точечных множеств, исследовать локальные свойства
отображений. Понятие окрестности используется при определении
предела, непрерывности, дифференцируемости функции.
2. Чему равна длина отрезка, соответствующего на числовой прямой
множеству решений неравенства ![]() ? Найдите координаты
середины этого отрезка.
? Найдите координаты
середины этого отрезка.
3. Известно, что переменная принимает все значения из промежутка
![]() . Задайте эту переменную с помощью неравенства,
содержащего модуль.
. Задайте эту переменную с помощью неравенства,
содержащего модуль.
4. Значения переменной ![]() находятся на числовой прямой от точки
с координатой 1,5 на
расстоянии меньшем, чем 0,2. Задайте эту переменную с помощью
неравенства, содержащего знак модуля.
находятся на числовой прямой от точки
с координатой 1,5 на
расстоянии меньшем, чем 0,2. Задайте эту переменную с помощью
неравенства, содержащего знак модуля.
Практическая компонента
I. 1. Дано утверждение:
а) "расстояние между точками ![]() и 3 меньше 0,1;
и 3 меньше 0,1;
![]()
![]()
б) "расстояние между точками ![]() и -0,2 не больше 0,01;
и -0,2 не больше 0,01;
![]() ";
";
в) "расстояние между точками ![]() и 1 больше 2";
и 1 больше 2";
г) "расстояние между точками ![]() и
и ![]() меньше
меньше ![]() ".
".
Записать его, i) используя знак принадлежности и обозначения окрестности в виде интервала; ii) используя неравенства с модулем; iii) используя двойные неравенства или системы и совокупности неравенств.
2. Найдите пересечение окрестности точки с координатой 5 радиуса 0,2 с окрестностью точки с координатой 4 радиуса 0,9.
3. Укажите непересекающиеся окрестности точек с координатами 3 и 2,9 (3 и 2,99).
4. Запишите тремя способами следующие окрестности:
а) окрестность точки с координатой 2,5 радиуса 0,3;
б) проколотую окрестность точки с координатой 2,5 радиуса 0,3 (точки "-3,7" радиуса 0,02).
5. Найдите пересечение всех окрестностей точки с координатой 5 и пересечение всех проколотых окрестностей этой точки.
6. Найдите наибольшую ![]() -окрестность точки
-окрестность точки ![]() , в которой
а)
, в которой
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
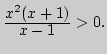
Теоретическая компонента
I. 1. Доказать утверждения:
а) объединение любой совокупности окрестностей одной и той же точки есть окрестность этой точки;
б) пересечение любой конечной совокупности окрестностей одной и той же точки есть окрестность этой точки.
II. 2. Пусть ![]() -подмножество числовой прямой,
-подмножество числовой прямой, ![]() -
множество предельных точек множества
-
множество предельных точек множества ![]() . Привести примеры таких
множеств, которые удовлетворяют соотношению: а)
. Привести примеры таких
множеств, которые удовлетворяют соотношению: а) ![]() б)
б) ![]() и
и
![]() в)
в) ![]() и
и
![]() г)
г)
![]() и
и
![]() ; д)
; д)
![]()
3. Привести пример множества, имеющего а) ровно одну предельную точку; б) ровно шесть предельных точек.
4. Может ли множество, состоящее только из изолированных точек, иметь предельные точки?
5. Доказать, что непустое пересечение любого семейства замкнутых множеств замкнуто.
6. Привести пример последовательности замкнутых множеств ![]() такой, что множество
такой, что множество
![]() не замкнуто;
в частности, чтобы множество
не замкнуто;
в частности, чтобы множество ![]() было интервалом.
было интервалом.
7. Привести пример последовательности открытых множеств ![]() такой, что множество
такой, что множество
![]() не открыто;
в частности, множество
не открыто;
в частности, множество ![]() - отрезок.
- отрезок.
8. Найдите множества предельных точек для
![]()
9. Найдите замыкания множеств
![]()
Знания: понятие верхней и нижней границы (грани) множества. Замкнутость множества верхних и нижних границ множества. Теорема существования граней. Характеристическое свойство граней. Теорема существования корня.
Умения: доказывать замкнутость множества верхних и нижних
границ множества, теорему существования корня, теорему
существования граней.
Приводить 10 примеров верхней и нижней границ множества.
![\begin{picture}(32.00,11.00)
\put(16.00,8.00){\makebox(0,0)[cc]{10}}
\emline{5.0...
...}{8.00}{7}{27.00}{5.00}{8}
\emline{27.00}{5.00}{9}{5.00}{5.00}{10}
\end{picture}](img849.png)
Мотивация. 1. Даны множества
![]() ;
;
![]() Перечислите элементы каждого
множества. Укажите число, превосходящее элементы множества
Перечислите элементы каждого
множества. Укажите число, превосходящее элементы множества ![]()
![]() ; число, не превосходящее. Единственны ли такие числа?
; число, не превосходящее. Единственны ли такие числа?
2. Какое свойство множества
![]() определяет следующее
высказывание:
определяет следующее
высказывание:
а)
![]() такое, что
такое, что
![]()
![]() ;
(1)
;
(1)
б)
![]() такое, что
такое, что
![]()
![]() .
(2)
.
(2)
3. Для каждого из следующих множеств укажите числа ![]() ,
удовлетворяющие высказыванию (1): а)
,
удовлетворяющие высказыванию (1): а) ![]() б)
б)
![]() в)
в) ![]() г)
г)
![]() д)
д)
![]() Для всех ли множеств существуют числа
Для всех ли множеств существуют числа ![]() ,
удовлетворяющие высказыванию (2)?
,
удовлетворяющие высказыванию (2)?
3. Назовите наибольший (наименьший) элемент множества, если он
существует: а)
![]() б)
б) ![]() в)
в) ![]() г)
г)
![]() д)
д)
![]() .
.
Теоретическая компонента
I. 1. Доказать, что множество
![]() ограничено
тогда и только тогда, когда существует такое
ограничено
тогда и только тогда, когда существует такое ![]() , что для
, что для
![]()
2. Всегда ли пересечение неограниченных множеств есть неограниченное множество?
II. 3. Доказать, что если ![]() и
и ![]() - ограниченные
множества, то их пересечение (объединение) - ограниченное
множество. Доказать, что объединение конечного числа отрезков
- ограниченные
множества, то их пересечение (объединение) - ограниченное
множество. Доказать, что объединение конечного числа отрезков
![]() есть ограниченное множество.
есть ограниченное множество.
4. Пусть множества ![]() и
и ![]() ограничены сверху, причем
ограничены сверху, причем
![]() . Следует ли из этого, что
. Следует ли из этого, что ![]() ? Какое условие
следует добавить, чтобы вложение выполнялось?
? Какое условие
следует добавить, чтобы вложение выполнялось?
5. Доказать, что если множества ![]() и
и ![]() таковы, что
выполняется условие
таковы, что
выполняется условие ![]() и множество
и множество ![]() ограничено, то
справедливы неравенства
ограничено, то
справедливы неравенства
![]() и
и
![]() .
.
6. Приведите пример числового множества ![]() , для которого
, для которого
![]()
![]() но которое не совпадает с отрезком
но которое не совпадает с отрезком
![]() .
.
7. Для каких числовых множеств
![]() ?
?
III. 8. Пусть ![]() - множество чисел вида
- множество чисел вида ![]() , где
, где
![]() Покажите, что
Покажите, что
![]()
![]()
9. Пусть ![]() - множество чисел вида
- множество чисел вида ![]() где
где
![]()
![]()
![]() - множество чисел вида
- множество чисел вида
![]() ;
; ![]() - множество чисел вида
- множество чисел вида ![]()
![]() Проверьте, всегда ли
Проверьте, всегда ли
а)
![]()
![]()
б)
![]()
в)
![]()
![]()
Практическая компонента
I. 1. Найти ![]() и
и
![]() если
а)
если
а)
![]() б)
б)
![]()
в)
![]() г)
г)
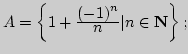 д)
д)
![]()
II. 2. Найти ![]() и
и
![]() если
если
а)
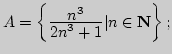
б)
![]()
в)
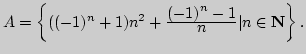
3. Пусть
![]() Доказать, что множество
Доказать, что множество ![]() не имеет ни наименьшего, ни наибольшего элемента. Найти
не имеет ни наименьшего, ни наибольшего элемента. Найти
![]() и
и
![]()
III. 4. Ограничены или нет множества, если ограничены,
найти точные границы:
![]()
![]()
Знания: понятие функции. Система обозначений. Типы отображений (инъекция, сюръекция, биекция). Способы задания функций (аналитический, табличный, графический, словесный). Понятие композиции функций. Ассоциативный закон композиции. Контрпример для коммутативного закона. Понятие обратной функции.
Умения: доказывать ассоциативный закон композиции функций, приводить контрпример для коммутативного закона. Приводить примеры различных типов отображений, способов задания функций (10 примеров). Понятие обратной функции (10 примеров).
![\begin{picture}(87.00,19.00)
\put(51.00,8.00){\makebox(0,0)[cc]{10}}
\emline{40....
...00}{15}{62.00}{5.00}{16}
\emline{62.00}{5.00}{17}{40.00}{5.00}{18}
\end{picture}](img991.png)
Навыки: построение графиков элементарными средствами.
Мотивация. 1. История возникновения понятия функции.
2. История преподавания функциональных понятий в школе. 3. Функции
описывают реальные процессы. 4. Функции - один из основных
объектов изучения в школьном курсе математики.
Теоретическая компонента
I. 1. Пусть ![]() и
и ![]() - множества из области определения
функции
- множества из области определения
функции ![]() . Доказать, что
. Доказать, что
![]()
II. 2. Пусть ![]() и
и ![]() - множества из области
определения функции
- множества из области
определения функции ![]() . Доказать, что а)
. Доказать, что а)
![]() б)
б)
![]() в)
в)
![]() где
где ![]() - взаимнооднозначное отображение.
- взаимнооднозначное отображение.
3. Пусть ![]() - множество из области определения функции
- множество из области определения функции
![]() Как соотносятся множества
Как соотносятся множества ![]() и
и ![]() ? Доказать,
что
? Доказать,
что
![]()
4. При каких ![]() и
и ![]() функция
функция ![]() имеет обратную и
совпадает с ней?
имеет обратную и
совпадает с ней?
5. При каких
![]() функция
функция ![]()
![]() совпадает
со своей обратной?
совпадает
со своей обратной?
Практическая компонента
I. 1. Рассмотреть функцию, которая определяется по
следующему закону:
![]() ставит в соответствие число
ставит в соответствие число
![]() , равное квадрату
, равное квадрату ![]() -го десятичного знака после запятой при
разложении числа
-го десятичного знака после запятой при
разложении числа ![]() в десятичную дробь. Определите
в десятичную дробь. Определите ![]()
![]()
2. Дана функция
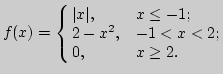 Постройте ее график.
Найдите
Постройте ее график.
Найдите ![]()
![]()
![]()
![]()
![]()
3. Пусть ![]()
![]() Какие из следующих функций
Какие из следующих функций
![]() задают инъективное (сюръективное, биективное)
отображение: а)
задают инъективное (сюръективное, биективное)
отображение: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д) ![]() е)
е)
![]() ?
?
4. Пусть
![]()
![]() Найти а)
Найти а)
![]() б)
б)
![]() в)
в)
![]() (
(![]() композиций); г)
композиций); г)
![]() (
(![]() композиций).
композиций).
5. Пусть ![]() определена на множестве
определена на множестве ![]() . Каковы
области определения функций
. Каковы
области определения функций ![]()
![]()
![]()
![]()
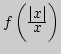 ?
?
6. Найти обратные функции и построить их графики:
а)
![]() б)
б)
![]()
![]() в)
в) ![]()
![]()
7. Пусть ![]() Найти множество на прямой
Найти множество на прямой ![]() ,
являющееся образом множества:
,
являющееся образом множества: ![]()
![]()
![]()
![]()
![]()
![]()
![]() Найти множество на оси
Найти множество на оси
![]() , являющееся прообразом множества
, являющееся прообразом множества ![]()
![]()
![]()
Прикладная компонента
I. 1. Окно имеет форму прямоугольника со сторонами ![]() и
и
![]() , на котором построен полукруг радиуса
, на котором построен полукруг радиуса
![]() Написать
аналитическое выражение
Написать
аналитическое выражение ![]() для площади части окна, отсекаемой
прямой, параллельной основанию прямоугольника и отстоящей от него
на расстоянии
для площади части окна, отсекаемой
прямой, параллельной основанию прямоугольника и отстоящей от него
на расстоянии ![]() .
.
2. Выразите полную поверхность цилиндра, вписанного в шар
радиуса ![]() , как функцию высоты. Найти обратную функцию и выделить
ее однозначные ветви.
, как функцию высоты. Найти обратную функцию и выделить
ее однозначные ветви.
3. Парашютист падает в свободном падении ![]() сек, после чего
открывает парашют и падает
сек, после чего
открывает парашют и падает ![]() сек с постоянной скоростью
сек с постоянной скоростью ![]() Написать выражение функции
Написать выражение функции ![]() пути, пройденного парашютистом
за время
пути, пройденного парашютистом
за время ![]() .
.
4. Имеются два куска сплава меди и цинка с процентным
содержанием меди в них ![]() % и
% и ![]() % соответственно. Сплавив эти
куски вместе, получили сплав с процентным содержанием меди в нем
% соответственно. Сплавив эти
куски вместе, получили сплав с процентным содержанием меди в нем
![]() %. Выразите
%. Выразите ![]() как функцию отношения масс этих кусков.
как функцию отношения масс этих кусков.
Знания: понятие основной элементарной функции;
элементарные
функции, типы (монотонные, периодические, ограниченные, четные,
нечетные). Классификация элементарных функций: многочлены,
рациональные функции, иррациональные, трансцендентные, неявные
алгебраические функции. Понятие декартовой, полярной,
параметрической системы координат на плоскости, переход из одной
системы координат в другую.
Умения: приводить примеры представителей различных типов элементарных функций (10 примеров), различных классов элементарных функций (10 примеров), функций, заданных в декартовой, полярной и параметрической системах координат (10 примеров).
Владеть методами преобразования графиков. Уметь построить график
функции, представляющей собой сумму, произведение, композицию и
обращение некоторых основных элементарных функций, например:
![]()
![]()
![]() Построение
графиков элементарных функций в декартовой, полярной
системах координат, в параметрических координатах. Уметь
приводить примеры непрерывного, периодического и другого
продолжения функции.
Построение
графиков элементарных функций в декартовой, полярной
системах координат, в параметрических координатах. Уметь
приводить примеры непрерывного, периодического и другого
продолжения функции.
Навыки: построение графиков основных элементарных функций:
степенной, показательной, логарифмической, тригонометрических,
обратных тригонометрических;
навыки исследования квадратичной функции, перехода от
одной системы координат к другой.
Методы: метод продолжения.
![\begin{picture}(144.00,19.00)
\put(48.00,8.00){\makebox(0,0)[cc]{10}}
\emline{37...
...01}{9.04}{34}
\put(112.00,5.00){\dashbox{2.00}(32.00,8.00)[cc]{ }}
\end{picture}](img1051.png)
Мотивация. 1. Исторические задачи и факты, приводящие к понятию конкретной основной элементарной функции.
2. Описание реальных процессов, которые моделируют элементарные функции на некотором сужении области определения (равномерных, равноускоренных, периодических, органического роста).
Теоретическая компонента
I. 1. Сформулировать, что означает, что функция ![]() не
является четной на промежутке
не
является четной на промежутке ![]() .
.
2. Докажите, что сумма двух непрерывных периодических функций, определенных на всей числовой прямой и не имеющих общих периодов, не является периодической.
3. Сформулировать утверждение: функция не является
ограниченной на множестве ![]() (не является монотонной на
промежутке
(не является монотонной на
промежутке ![]() ).
).
4. Доказать, что если график функции ![]() , определенной на
всей числовой прямой, симметричен относительно двух вертикальных
осей
, определенной на
всей числовой прямой, симметричен относительно двух вертикальных
осей ![]() и
и ![]() , то функция
, то функция ![]() периодическая (симметричен
относительно точки
периодическая (симметричен
относительно точки ![]() и прямой
и прямой ![]()
![]() ).
).
II. 5. Докажите, что любая функция с симметричной
относительно точки ![]() областью определения представляется (притом
единственным образом) в виде суммы четной и нечетной функции.
областью определения представляется (притом
единственным образом) в виде суммы четной и нечетной функции.
6. Существует ли функция, являющаяся одновременно четной и нечетной?
7. Докажите, что если ![]() - четная функция, а
- четная функция, а
![]() - нечетная, то
- нечетная, то
![]() - нечетная функция.
- нечетная функция.
8. Всегда ли разность двух возрастающих (убывающих) функций на
множестве ![]() является возрастающей (убывающей) функцией?
является возрастающей (убывающей) функцией?
9. Привести примеры немонотонных обратимых функций, указав обратные им функции.
10. Является ли произведение двух монотонных на ![]() функций
монотонной на
функций
монотонной на ![]() функцией?
функцией?
11. Доказать, что если функция ![]() возрастает на
возрастает на
![]() , а функция
, а функция ![]() убывает на
убывает на
![]() то функция
то функция ![]() возрастает на
возрастает на
![]()
12. Известно, что
![]() и
и
![]() . Следует ли
отсюда, что
. Следует ли
отсюда, что ![]() на
на ![]() ?
?
13. Следует ли из равенства
![]() , что
, что ![]() постоянна на
постоянна на ![]() ?
?
Практическая компонента
I. 1. Какие из следующих функций являются бесконечно
большими при
![]() , какие ограниченными, какие
неограниченными:
, какие ограниченными, какие
неограниченными:
а)
![]() б)
б)
![]() в)
в)
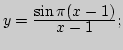 г)
г)
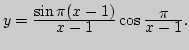
2. Какие из следующих функций ограничены снизу (сверху),
ограничены:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г) ![]() д)
д)
![]() е)
е)
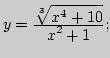 ж)
ж)
![]() з)
з)
![]() и)
и)
![]() к)
к)
![]() л)
л)
![]()
3. Дана функция
![]() Найти ее
наибольшее и наименьшее значения и значения аргумента, при которых
они достигаются.
Найти ее
наибольшее и наименьшее значения и значения аргумента, при которых
они достигаются.
4. Продолжить функции а) четным образом:
![]()
![]() б) нечетным образом:
б) нечетным образом:
![]()
![]()
5. Продолжить нечетным образом функцию
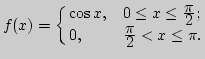
6. Периодически продолжить функцию ![]()
![]() на всю ось
на всю ось ![]()
II. 7. Доказать, что функция не является периодической:
а) ![]() б)
б)
![]() в)
в) ![]() г)
г)
![]()
8. Найдите ось симметрии для графиков функций:
а)
![]() б)
б) ![]() Найдите центр
симметрии функции: а)
Найдите центр
симметрии функции: а)
![]() б)
б)
![]()
9.Доказать, что функции являются монотонными: а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]() д)
д)
![]() е)
е)
![]()
10. Найти множество значений функции: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() е)
е)
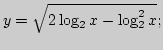 ж)
ж)
![]()
11. Точки ![]() и
и ![]() имеют полярные координаты
имеют полярные координаты
![]() и
и
![]() соответственно. Найдите длину отрезка
соответственно. Найдите длину отрезка ![]() .
.
12. На плоскости выбрана декартова (полярная) система координат. Изобразить на плоскости множество точек, имеющих
а) первую координату, равную 2;
![]()
б) вторую координату, равную 1;
![]()
Деятельностная компонента
I. 1. Построить графики функций:
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]() 5)
5)
![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]() 9)
9) ![]() 10)
10) ![]() 11)
11)
![]() 12)
12)
![]()
2. Построить графики функций: 1) ![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]() 5)
5)
![]() 6)
6)
![]() 7)
7)
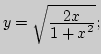 8)
8)
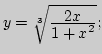 9)
9)
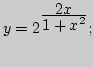 10)
10)
![]() 11)
11)
![]() 12)
12)
![]() 13)
13)
![]() 14)
14)
![]() 15)
15)
![]() 16)
16)
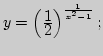 17)
17)
![]() 18)
18)
![]() 19)
19) ![]() 20)
20)
![]() 21)
21)
![]() 22)
22)
![]() 23)
23)
![]() 24)
24)
![]() 25)
25) ![]()
3. Построить графики функций ![]() , заданных
параметрически: а)
, заданных
параметрически: а)
![]() б)
б)
![]() в)
в)
![]()
4. Построить графики функций, заданных в полярной системе
координат: а)
![]() ; б)
; б)
![]() в)
в) ![]() д)
д)
![]() д)
д) ![]()
5. Записать в полярных координатах уравнение и построить
график: а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
6. Изобразить графики уравнений: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() д)
д)
![]() е)
е)
![]()
Знания: последовательность как функция натурального
аргумента. Способы задания, некоторые приемы конструирования
последовательностей.
Способы задания: аналитический (арифметическая, геометрическая прогрессии), рекуррентный способ задания, числа Фибоначчи.
Умения: приводить примеры последовательностей, заданных
различными способами,
конструировать последовательности: непрерывные дроби, десятичные
дроби, числовые ряды, арифметические операции (10 примеров).
![\begin{picture}(66.00,15.00)
\put(50.00,8.00){\makebox(0,0)[cc]{10}}
\emline{39....
...00}{15}{61.00}{5.00}{16}
\emline{61.00}{5.00}{17}{39.00}{5.00}{18}
\end{picture}](img1177.png)
Мотивация. 1. Числовые последовательности представляют
собой аппарат, не заменимый при изучении бесконечных процессов, и
именно этим обусловлена их роль в математике.
2. Числовые ряды являются частным случаем последовательностей, новой формой изучения последовательности и ее предела.
3. Последовательности, в частности, арифметическая и геометрическая прогрессии, являются одним из объектов изучения в школьной математике.
4. Последовательность - частный случай функции. Какова область определения последовательности? Каким является ее множество значений? Какие способы изображения последовательностей существуют? Как найти расстояние между двумя членами последовательности?
Теоретическая компонента
I. 1. Привести пример последовательности ![]() ,
удовлетворяющей условию:
,
удовлетворяющей условию:
а)
![]()
б)
![]()
в)
![]() и
и
![]()
д)
![]()
2. Какое свойство последовательности определяет следующее высказывание:
а)
![]()
б)
![]()
3. Доказать, что если
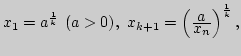 то
то
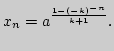
4. Найти общий член последовательности ![]() если
если
![]() и
и
![]() для
для
![]()
5. Существует ли последовательность ![]() такая, что для
такая, что для
![]()
![]() верно равенство
верно равенство
![]() ?
?
Практическая компонента
I. 1. Указать какой-либо номер ![]() такой, что для всех
такой, что для всех
![]() члены последовательности
члены последовательности ![]() удовлетворяют
заданному неравенству:
удовлетворяют
заданному неравенству:
а)
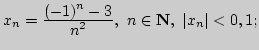
б)
![]()
в)
![]() (доказать и использовать неравенство
(доказать и использовать неравенство
![]() .
.
2. Задайте аналитически последовательность ![]() , если
, если
а)
![]()
б)
![]()
II. 3. Задайте аналитически последовательность ![]() ,
если
,
если
![]()
4. Доказать, что ![]() - геометрическая прогрессия:
- геометрическая прогрессия:
а)
![]()
б)
![]()
в)
![]()
Деятельностная компонента
I. 1. Изобразить геометрически (двумя способами)
последовательность ![]() : а)
: а)
![]() б)
б)
![]() в)
в)
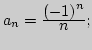 г)
г)
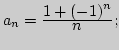 д)
д)
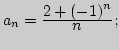 е)
е)
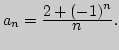
2. Какие из чисел ![]() являются членами последовательности
являются членами последовательности
![]() если
если
а)
![]()
б)
![]()
в)
![]()
3. Последовательность задана формулой
![]() .
.
а) Найти расстояние от точки 2 до точки
![]() на числовой прямой.
на числовой прямой.
б) Укажите номера членов последовательности, удаленных от точки 2 менее чем на 0,1; 0,02.
Знания: понятие предела последовательности, понятие бесконечно малой и бесконечно большой последовательности, теоремы о бесконечно малых последовательностях, понятие суммы числового ряда, расходимость гармонического ряда.
Умения: приводить примеры сходящихся и расходящихся
последовательностей (в частности, пример
![]() ). Доказывать теоремы о
бесконечно малых последовательностях. Уметь вычислять пределы
последовательностей:
). Доказывать теоремы о
бесконечно малых последовательностях. Уметь вычислять пределы
последовательностей: ![]()
![]()
![]()
![]()
![]()
![\begin{picture}(56.00,15.00)
\put(41.00,9.00){\makebox(0,0)[lc]{$\overline{\fora...
...00}{13}{33.00}{15.00}{14}
\emline{33.00}{5.00}{15}{5.00}{5.00}{16}
\end{picture}](img1223.png)
Мотивация. 1. Последовательность десятичных приближений (по
недостатку) к числу ![]() :
:
а)
![]()
б)
![]()
![]() отличается от
отличается от ![]() , эта разность становится сколь угодно
малой при неограниченном возрастании
, эта разность становится сколь угодно
малой при неограниченном возрастании ![]() .
.
2. Опишите поведение членов последовательностей (характер приближения последовательностей к 0) из примера 1 (деятельностная компонента, 12 вопрос).
3. Пусть
![]() Найдите, начиная с какого номера
Найдите, начиная с какого номера ![]() все
члены последовательности
все
члены последовательности
![]() будут
удалены от 0 на расстояние, меньшее
будут
удалены от 0 на расстояние, меньшее ![]() Решите задачу при
произвольном
Решите задачу при
произвольном
![]() Как записать данное свойство с помощью
неравенства с модулем? На языке окрестностей? Приведите
геометрическую иллюстрацию.
Как записать данное свойство с помощью
неравенства с модулем? На языке окрестностей? Приведите
геометрическую иллюстрацию.
Теоретическая компонента
I. 1. Постройте отрицание понятия предела
последовательности. Запишите на "
![]() " языке (на языке
окрестностей), что а) число
" языке (на языке
окрестностей), что а) число ![]() не является пределом
последовательности
не является пределом
последовательности ![]() б) никакое число
б) никакое число ![]() не является пределом последовательности
не является пределом последовательности
![]() Как изменится утверждение, если
Как изменится утверждение, если ![]()
![]() ?
?
2. Сформулируйте на "
![]() " языке отрицание того, что
" языке отрицание того, что
![]() - бесконечно большая последовательность.
- бесконечно большая последовательность.
II. 3. Докажите, пользуясь определением, что а)
![]() б)
б)
![]()
4. Докажите, что последовательности а)
![]() б)
б)
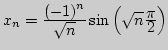 бесконечно малые.
бесконечно малые.
5. Доказать, что последовательность расходится: а) ![]() б)
б) ![]() в)
в)
![]() г)
г)
![]()
6. Известно, что
![]() Найдите
число точек последовательности, лежащих вне интервала
Найдите
число точек последовательности, лежащих вне интервала
![]()
7. Приведите примеры последовательности ![]() такой, что
такой, что
![]() и а)
и а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() е) последовательность
е) последовательность
![]()
![]() не имеет предела.
не имеет предела.
Знания: теорема о единственности предела последовательности, теоремы о переходе к пределу в неравенствах, арифметические операции над пределами (теоремы о пределе суммы, произведения, частного).
Умения: доказывать перечисленные теоремы, вычислять сумму
бесконечного числа членов убывающей геометрической прогрессии,
владеть методами раскрытия неопределенностей вида:
![]()
![]()
![]()
![]()
![]()
![]()
![\begin{picture}(66.00,16.00)
\put(42.00,11.00){\makebox(0,0)[lc]{$\sum\limits_{n...
....00}{17}{27.00}{6.00}{18}
\emline{27.00}{6.00}{19}{5.00}{6.00}{20}
\end{picture}](img1262.png)
Теоретическая компонента
II. 1. Пусть в некоторой окрестности точки ![]() находится
бесконечное множество членов последовательности
находится
бесконечное множество членов последовательности ![]() . Верно
ли, что: а)
. Верно
ли, что: а)
![]() б) никакая точка вне
этой окрестности не является пределом последовательности
б) никакая точка вне
этой окрестности не является пределом последовательности
![]() ?
?
2. Пусть
![]() и
и
![]() . Исследовать на сходимость
последовательность
. Исследовать на сходимость
последовательность ![]()
![]()
![]()
![]()
![]()
![]()
3. Верно ли, что если последовательность ![]() расходится,
то последовательность
расходится,
то последовательность ![]()
![]()
![]() а) сходится; б) расходится?
а) сходится; б) расходится?
4. Известно, что
![]() .
Следует ли отсюда, что а)
.
Следует ли отсюда, что а)
![]() б) хотя бы одна из
последовательностей стремится к нулю?
б) хотя бы одна из
последовательностей стремится к нулю?
5. Последовательность ![]() сходится и
сходится и
![]() последовательность
последовательность
![]() расходится. Доказать, что последовательность
расходится. Доказать, что последовательность
![]() расходится.
расходится.
6. Доказать, что: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() е)
е)
![]()
![]() ж)
ж)
![]()
![]()
Практическая компонента
1. Найти пределы последовательностей:
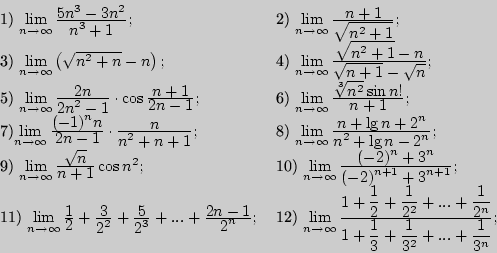
Знания: понятие ограниченной последовательности, теорема об ограниченности сходящейся последовательности, понятие монотонной последовательности, теорема Вейерштрасса.
Умения: приводить примеры ограниченных последовательностей,
монотонных последовательностей (10 примеров), доказывать
теорему об ограниченности сходящейся последовательности, теорему
Вейерштрасса, владеть логическим анализом теоремы.
![\begin{picture}(101.00,13.00)
\put(85.00,8.00){\makebox(0,0)[cc]{10}}
\emline{74...
...00}{25}{63.00}{5.00}{26}
\emline{63.00}{5.00}{27}{41.00}{5.00}{28}
\end{picture}](img1290.png)
Мотивация. 1. Верны ли высказывания:
- монотонная последовательность имеет предел;
- ограниченная последовательность имеет предел;
- сходящаяся последовательность является монотонной;
- сходящаяся последовательность является ограниченной.
Приведите примеры (контрпримеры).
2. Всегда ли неограничена расходящаяся последовательность?
3. Приведите пример неограниченной последовательности, не являющейся бесконечно большой.
Теоретическая компонента
II. 1. Докажите верные высказывания из пункта 1 раздела "Мотивация".
2. Пусть последовательность ![]() ограничена. Существуют
ли пределы
ограничена. Существуют
ли пределы
![]()
![]() , если последовательность
, если последовательность
![]() а) сходится; б) расходится.
а) сходится; б) расходится.
3. Доказать, что если ![]() и
и ![]() - ограниченные
последовательности, то ограничены и последовательности
- ограниченные
последовательности, то ограничены и последовательности
![]() где
где
![]()
4. Привести пример ограниченных последовательностей ![]() и
и ![]()
![]() таких, что последовательность
таких, что последовательность
![]() неограничена.
неограничена.
Практическая компонента
I. 1. Доказать, что последовательности ограничены:
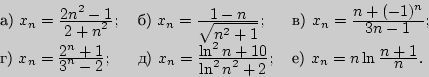
2. Доказать, что последовательности не ограничены:
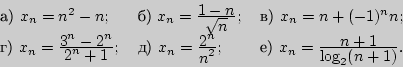
3. Доказать, что данная последовательность монотонна, начиная
с некоторого номера:
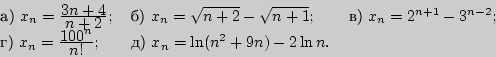
4. Доказать, что существуют пределы последовательностей:
а)
![]()
б)
![]()
в)
![]()
г)
![]() где
где
![]() ;
;
д)
![]()
Знания: понятие подпоследовательности как сужение функции
натурального аргумента, как композиции функций, теорема о
подпоследовательностях сходящейся последовательности, лемма
Больцано-Вейерштрасса.
Умения: приводить примеры подпоследовательностей,
доказывать теорему о подпоследовательностях сходящейся
последовательности, лемму Больцано-Вейерштрасса.
Методы: метод Больцано.
![\begin{picture}(25.00,13.00)
\put(5.00,5.00){\dashbox{2.00}(20.00,8.00)[cc]{ }}
...
...}{21}{11.00}{10.00}{22}
\emline{11.00}{10.00}{23}{11.00}{8.00}{24}
\end{picture}](img1306.png)
Теоретическая компонента
II. 1. Привести пример последовательности, не имеющей ни одной сходящейся (к числу) подпоследовательности.
2. Привести пример неограниченной последовательности, имеющей сходящуюся (к числу) подпоследовательность.
3. Привести пример последовательностей ![]() и
и ![]() таких, что
таких, что
![]() но
но ![]() не
является подпоследовательностью последовательности
не
является подпоследовательностью последовательности ![]()
Практическая компонента
I. 1. Является ли последовательность ![]() подпоследовательностью последовательности
подпоследовательностью последовательности ![]() :
:
 x_n=n;
x_n=n;![]() 1) y_k=k^2+1;
1) y_k=k^2+1;![]() 2) y_k=k^2-4k+5;
2) y_k=k^2-4k+5;![]() x_n=2n;
x_n=2n;![]() 1) y_k=2^k;
1) y_k=2^k;![]() 2) y_k=2(k+(-1)^k);
2) y_k=2(k+(-1)^k);![]() x_n=1n;
x_n=1n;![]() 1) y_k=1k-k;
1) y_k=1k-k;![]() 2) y_k=13k-k.
2) y_k=13k-k.
![]()
2. Указать сходящуюся подпоследовательность последовательности
![]() : а)
: а) ![]() б)
б)
![]() в)
в)
![]()
Знания: понятие частичного предела последовательности, теорема о частичных пределах сходящейся последовательности, понятие верхнего и нижнего предела последовательности, необходимое и достаточное условия существования предела.
Умения: доказывать теорему о частичных пределах сходящейся
последовательности, приводить примеры верхнего и нижнего пределов
последовательности.
Теоретическая компонента
II. 1. Доказать, что всякая монотонная последовательность имеет только один частичный предел.
2. Доказать, что для того, чтобы ![]() (число,
(число, ![]() ,
,
![]() ) было частичным пределом последовательности, необходимо
и достаточно, чтобы в любой окрестности
) было частичным пределом последовательности, необходимо
и достаточно, чтобы в любой окрестности ![]() содержалось бесконечно
много членов этой последовательности.
содержалось бесконечно
много членов этой последовательности.
Практическая компонента
1. Найти все частичные пределы последовательности ![]() а)
а)
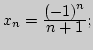 б)
б) ![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() е)
е)
![]()
Знания: предельная точка и сходящиеся последовательности, понятие проколотой окрестности, определение предела функции в точке на языке окрестностей.
Умения: записывать различные варианты
![]() -определений (
-определений (
![]()
![]()
![\begin{picture}(33.00,15.00)
\put(19.00,10.00){\makebox(0,0)[cc]{$\lim f$}}
\eml...
...{15.00}{5}{33.00}{15.00}{6}
\emline{33.00}{5.00}{7}{5.00}{5.00}{8}
\end{picture}](img1325.png)
Мотивация. 1. Понятие предела - одно из основных фундаментальных понятий математики. На идейном уровне понятие предела отображения определяется так, что достаточная близость элементов в одном множестве при отображении обеспечивает заданную близость элементов в другом множестве. На основе понятия предела определяются понятия непрерывности, равномерной непрерывности, дифференцируемости.
2. История формирования понятия предела в математике.
3. При рассмотрении предела на бесконечности возможна опора на имеющийся опыт, связь с жизнью (процесс остывания нагретого чайника - его температура приближается к комнатной; учащиеся знакомы с горизонтальными асимптотами у некоторых графиков).
4. Серия подводящих задач (предложена А.Г.Мордковичем, А.Е.Мухиным):
1) Пусть.
а) Найдите множество значений, на которое отображается множество значений
, удовлетворяющих неравенству
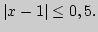
б) Переменнаяудовлетворяет неравенству
Следует ли из этого, что для соответствующих значений
верно неравенство
?
2) Пусть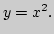
а) Известно, чтоБудут ли соответствующие значения
удовлетворять соотношениям:
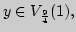
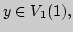
? Записать при помощи неравенств с модулем и изобразить графики.
б) ПустьНайдите на оси
множество, образом которого будет данная окрестность. Следует ли из того, что
удовлетворяет неравенству
, где
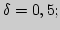
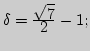
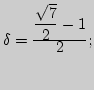
что соответствующие значения
?
3) Постройте график функцииНайдите значение
, для которого
Для любого
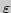
на оси ординат выделите интервал
и найдите на оси
множество, образом которого будет выделенный интервал.
Пусть это будет интервали
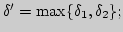
Следует ли при выбранных
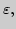
и
из неравенства
неравенство
(из неравенства
неравенство
)?
4) Указать наибольшее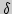
, при котором для всех точек
из
-окрестности точки
выполняется неравенство
для
0,01; 0,001, если а)
; б)
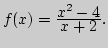
Теоретическая компонента
I. 1. Записать утверждение в предельной форме и изобразить эскиз графика функции, удовлетворяющей данному утверждению:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
II. 2. Определить, при каких ![]() из неравенства
из неравенства
![]() следует неравенство
следует неравенство
![]() если
если
а)
![]()
б)
![]()
в)
![]()
г)
![]()
3. Определить, при каких ![]() из неравенства
из неравенства ![]() следует неравенство: а)
следует неравенство: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
4. При каких ![]() из неравенства
из неравенства ![]() следует
неравенство
следует
неравенство
![]() , где
, где
![]() ?
?
5. Пользуясь определением предела функции в точке, докажите
следующие утверждения:
| 1)
|
2)
|
3)
|
| 4)
|
5)
|
6)
|
| 7)
|
8)
|
9)
|
| 10)
|
11)
|
12)
|
| 13)
|
Знания: понятие односторонних пределов функции в точке,
предел функции на языке последовательностей, эквивалентность двух
определений предела функции, достаточное условие несуществования
предела функции, теоремы о пределе функции (о единственности
предела, о промежуточной переменной, о пределе суммы,
произведения и частного функций), замечательные пределы.
Умения: приводить примеры односторонних пределов функций в
точке (10 примеров), доказывать эквивалентность определения
предела функции на языке окрестностей и последовательностей,
доказывать теоремы о пределе функции.
Методы: метод "от противного".
![\begin{picture}(141.00,15.00)
\put(79.00,10.00){\makebox(0,0)[cc]{10}}
\emline{6...
...0){\dashbox{2.00}(20.00,8.00)[cc]{$\bar B\Longrightarrow \bar A$}}
\end{picture}](img1393.png)
Мотивация. Серия задач. 1. На рисунке изображены графики
функций. Для каждой из них установить, имеет ли она предел при
![]() и, если имеет, то чему он равен:
и, если имеет, то чему он равен:
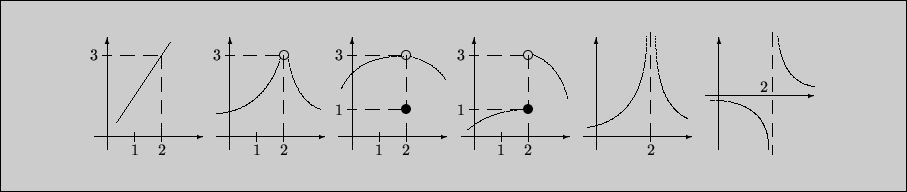
2. Привести примеры функций (задать аналитически и построить график), для которых в некоторой точке:
а) функция определена в точке, но не имеет предела в этой точке;
б) не существует предела и функция не определена в точке;
в) не существует предела и функция в точке не определена, хотя функция определена в проколотой окрестности точки;
г) существует и предел, и значение, но они между собой не равны.
Теоретическая компонента
II. 1. Пользуясь определением предела в форме Гейне, доказать, что функция Дирихле не имеет предела ни в одной точке.
2. Верно ли, что предел функции, принимающей только положительные значения, может быть только положительным числом?
3. Существует ли функция ![]() , которая не имеет предела ни в
одной точке оси
, которая не имеет предела ни в
одной точке оси ![]() и имеет предел на бесконечности?
и имеет предел на бесконечности?
4. Даны две функции ![]() и
и ![]() , причем
, причем ![]() и
и
![]() Доказать, что
Доказать, что
![]()
5. Доказать, что функция, имеющая предел в точке ![]() ,
ограничена в некоторой окрестности точки
,
ограничена в некоторой окрестности точки ![]() и сохраняет знак
предела функции в точке
и сохраняет знак
предела функции в точке ![]() во всех точках некоторой проколотой
окрестности точки
во всех точках некоторой проколотой
окрестности точки ![]()
![]()
6. Найти предел функции
![]() в точке
в точке
![]() , воспользовавшись определением предела функции на языке
последовательностей (на
, воспользовавшись определением предела функции на языке
последовательностей (на
![]() -языке).
-языке).
7. Пусть функции ![]() и
и ![]() не имеют предела в точке
не имеют предела в точке
![]() Следует ли отсюда, что
Следует ли отсюда, что ![]() и
и ![]() также не
имеют предела в этой точке?
также не
имеют предела в этой точке?
II. 8. Может ли существовать предел
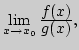 если
если ![]()
![]() ?
?
9. Доказать, что если для любой последовательности ![]() ,
сходящейся к точке
,
сходящейся к точке ![]() последовательность
последовательность ![]() сходится, то
сходится, то
![]() существует.
существует.
10. Доказать, что если из любой последовательности ![]() ,
сходящейся к точке
,
сходящейся к точке ![]() , можно выделить подпоследовательность
, можно выделить подпоследовательность
![]() для которой
для которой
![]() , то
, то
![]()
11. Сформулировать утверждения (на
![]() -языке) и привести
примеры: а)
-языке) и привести
примеры: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() е)
е)
![]() ж)
ж)
![]()
12. Пусть
![]()
![]() Показать, что
Показать, что
![]()
![]() но
но
![]() не существует. Почему не применима теорема о
пределе сложной функции?
не существует. Почему не применима теорема о
пределе сложной функции?
Практическая компонента
I. 1. Вычислите предел, если известно, что
![]()
![]() : а)
: а)
![]() б)
б)
![]() в)
в)
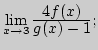 г)
г)
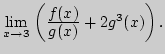
2. Найдите пределы функций:
| 1)
|
2)
|
| 3)
|
4)
|
| 5)
|
6)
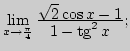 |
7)
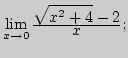 |
8)
|
9)
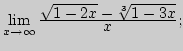 |
10)
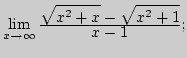 |
| 11)
|
12)
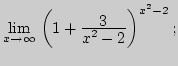 |
13)
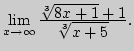 |
Прикладная компонента
1. Дан правильный треугольник со стороной ![]() . Из трех его высот
строится новый правильный треугольник и так
. Из трех его высот
строится новый правильный треугольник и так ![]() раз. Найдите предел
суммы всех площадей треугольников при
раз. Найдите предел
суммы всех площадей треугольников при
![]()
2. В круг радиуса ![]() вписан квадрат, в квадрат вписан круг, в
этот круг опять вписан квадрат и так
вписан квадрат, в квадрат вписан круг, в
этот круг опять вписан квадрат и так ![]() раз. Найдите предел
суммы площадей всех кругов и предел суммы площадей всех квадратов
при
раз. Найдите предел
суммы площадей всех кругов и предел суммы площадей всех квадратов
при
![]()
Деятельностная компонента
I. 1. Построить график функции и найти предел при
![]() , если он существует:
, если он существует:
а) ![]()
![]() б)
б)
![]()
![]() в)
в)
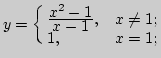
![]() г)
г)
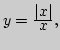
![]()
![]()
2. Нарисовать график функции в окрестности точки ![]() если:
если:
а) ![]()
![]()
![]()
б) ![]()
![]()
![]() не существует;
не существует;
в) ![]()
![]() не
существует,
не
существует,
![]()
г) ![]()
![]()
![]()
![]()
д) ![]()
![]() не существует,
не существует,
![]()
е)
![]()
![]()
![]()
ж) ![]()
![]()
![]()
![]()
Знания: определение непрерывности функции в точке и на множестве, непрерывность элементарных функций, теорема о непрерывности сложной функции, теоремы об арифметических операциях над непрерывными функциями (сумма, произведение, частное).
Умения: доказывать непрерывность элементарных функций,
доказывать теорему о непрерывности сложной функции,
теоремы об арифметических операциях над непрерывными функциями.

Мотивация. В задачах вопроса 19 разделов "Мотивация",
"Деятельностная компонента" определить, являются ли функции
непрерывными.
Теоретическая компонента
I. 1. Сформулируйте определение непрерывной функции на
трех "языках": а) на языке пределов; б) на "
![]() "-языке; в) с
использованием приращения функции. Докажите их эквивалентность.
"-языке; в) с
использованием приращения функции. Докажите их эквивалентность.
II. 2. Что можно сказать о непрерывности в точке ![]() функций
функций ![]()
![]()
![]() если
если
а) функция ![]() непрерывна в точке
непрерывна в точке ![]() , а
, а ![]() разрывна в
точке
разрывна в
точке ![]() ;
;
б) функции ![]() и
и ![]() разрывны в точке
разрывны в точке ![]()
Привести примеры.
3. Построить пример функций ![]() и
и ![]() таких, что
таких, что
![]() непрерывна в точке
непрерывна в точке ![]() , а
, а ![]() разрывна в точке
разрывна в точке
![]()
4. Пусть ![]() . Будет ли непрерывна функция
. Будет ли непрерывна функция ![]() в
точке
в
точке ![]() если
если ![]() непрерывна в точке
непрерывна в точке ![]() , а функция
, а функция
![]() разрывна в точке
разрывна в точке ![]() ?
?
5. Доказать, что функция Римана
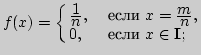 где
где ![]() - взаимно простые числа, разрывна при каждом рациональном
значении
- взаимно простые числа, разрывна при каждом рациональном
значении ![]() и непрерывна при каждом иррациональном значении
и непрерывна при каждом иррациональном значении ![]() .
.
6. Доказать, что функция Дирихле
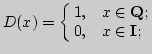 разрывна в каждой точке.
Исследовать на непрерывность функцию
разрывна в каждой точке.
Исследовать на непрерывность функцию
![]()
7. Привести пример функции, непрерывной только а) в одной
точке; б) в двух (в ![]() ) точках.
) точках.
8. Доказать непрерывность функций в точке на "
![]() "
языке: а)
"
языке: а) ![]()
![]() б)
б) ![]()
![]() в)
в) ![]()
![]() г)
г)
![]()
![]()
9. Доказать непрерывность функции в точке с использованием
приращения функции: а)
![]() на
на ![]() ; б)
; б)
![]() на
на ![]() ; в)
; в) ![]() на
на ![]() ; г)
; г)
![]() на
на ![]() .
.
10. Доказать непрерывность функции на языке
пределов:
а)
![]() на
на ![]() б)
б)
![]() на
на ![]() в)
в) ![]() на
на ![]()
Практическая компонента
I. 1. Исследовать функции на непрерывность:
а)
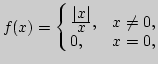 б)
б)
![]() в)
в)
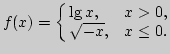
2. Установить, существует или нет значение ![]()
![]() и
и ![]() ,
при котором функция
,
при котором функция ![]() непрерывна в точке
непрерывна в точке ![]() :
:
а)
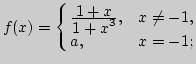
![]() б)
б)
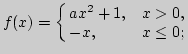
![]()
в)
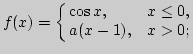
![]() г)
г)
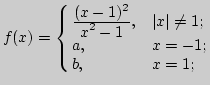
д)
![$f(x)=\cases{{\displaystyle x\cos{x\over 2}\over\displaystyle \sin x},&
$x\in\le...
...over\displaystyle 2}\right],\ x\ne0,\ x\ne\pi;$\cr
a,&$x=0;$\cr
b,&$x=\pi.$\cr}$](img1521.png)
Деятельностная компонента
1. Найти точки разрыва функции, установить их род, найти скачки функции в соответствующих точках разрыва I рода, построить график функции:
1)
![]() 2)
2)
![]() 3)
3)
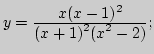
4)
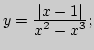 5)
5)
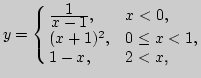 6)
6)
![]()
7)
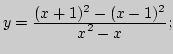 8)
8)
![]() 9)
9)
![]()
10)
![]()
2. Приведите пример функции, имеющей 3 вертикальные асимптоты
и горизональную асимптоту ![]()
Прикладная компонента
1. Требуется изготовить металлическую квадратную пластинку со
сторонами ![]() см. В каких пределах допустимо изменять сторону
пластинки
см. В каких пределах допустимо изменять сторону
пластинки ![]() , чтобы ее площадь отличалась от проектной площади на
, чтобы ее площадь отличалась от проектной площади на
![]() см
см![]() не более чем на
не более чем на ![]() см
см![]() ?
?
2. Пусть требуется произвести измерение площади и периметра
квадратной пластинки, длина стороны которой равна ![]() , с заданной
степенью точности
, с заданной
степенью точности ![]()
![]() . С какой точностью требуется при
этом измерять длину стороны пластинки?
. С какой точностью требуется при
этом измерять длину стороны пластинки?
3. Имеется участок земли в форме прямоугольника со сторонами
длин 15 и ![]() . С какой степенью точности нужно измерить сторону
. С какой степенью точности нужно измерить сторону
![]() прямоугольника, чтобы вычислить с точностью до 0,01 его
а) периметр; б) площадь.
прямоугольника, чтобы вычислить с точностью до 0,01 его
а) периметр; б) площадь.
4. Демидович Б.П. Сборник задач. М.: Наука, 1990. № 733. С. 83.
Знания: теоремы Больцано-Коши о промежуточных значениях, теоремы Вейерштрасса об ограниченности функций. Равномерная непрерывность функции на множестве. Теорема Кантора.
Умения: доказывать данные теоремы (несколько способов),
проводить логический анализ теоремы, геометрическая иллюстрация
теорем, приводить частные примеры и контрпримеры.
Методы: метод Больцано, метод введения вспомогательной
функции.
![\begin{picture}(152.00,22.00)
\put(87.00,9.00){\makebox(0,0)[cc]{$T$}}
\put(81.0...
...)[cc]{${\buildrel{\displaystyle +f}\over{\ \longrightarrow \ }}$}}
\end{picture}](img1537.png)
Теоретическая компонента
1. Доказать, что если функция определена и непрерывна на отрезке, то множество ее значений - отрезок.
2. Привести пример разрывной функции, определенной на отрезке и имеющей в качестве множества значений отрезок.
3. Привести пример функции, непрерывной на интервале ![]() ,
множеством значений которой является а) интервал; б) полуотрезок;
в) отрезок; г) полупрямая.
,
множеством значений которой является а) интервал; б) полуотрезок;
в) отрезок; г) полупрямая.
4. Доказать, что непрерывная на отрезке функция, не имеющая на этом отрезке ни одного внутреннего экстремума, монотонна. Привести пример, показывающий, что для разрывных функций это неверно.
5. Доказать, что если функция определена на отрезке ![]() и
на этом отрезке принимает каждое промежуточное значение только 1
раз, то она непрерывна на
и
на этом отрезке принимает каждое промежуточное значение только 1
раз, то она непрерывна на ![]()
6. Функция ![]() непрерывна на интервале
непрерывна на интервале ![]() ;
;
![]()
![]() Доказать,
что для любого
Доказать,
что для любого ![]() существует
существует ![]() такое, что
такое, что
![]()
7. Доказать, что функция ![]() , удовлетворяющая условию
Гельдера-Липшица, равномерно непрерывна на множестве
, удовлетворяющая условию
Гельдера-Липшица, равномерно непрерывна на множестве ![]() :
:
Прикладная компонента
1. Доказать, что уравнения ![]() а) имеет хотя бы
один корень на интервале
а) имеет хотя бы
один корень на интервале ![]() ; б) имеет не менее трех корней
на
; б) имеет не менее трех корней
на ![]()
2. Доказать, что любой многочлен нечетной степени имеет хотя бы один действительный корень.
3. Доказать, что если многочлен четной степени принимает хотя бы одно значение, противоположное по знаку коэффициенту старшего члена, то он имеет не более двух действительных корней.
4. Будет ли ограниченной функция
![]() рассматриваемая на отрезке
рассматриваемая на отрезке ![]() ? Существуют ли такие
значения, при которых функция принимает наибольшее (наименьшее)
значение?
? Существуют ли такие
значения, при которых функция принимает наибольшее (наименьшее)
значение?
5. Построить логическое отрицание определения равномерной
непрерывности функции ![]() на множестве
на множестве
![]() Доказать
отсутствие равномерной непрерывности функции
Доказать
отсутствие равномерной непрерывности функции
![]() на
промежутке
на
промежутке ![]()