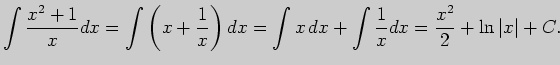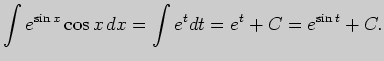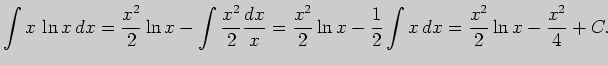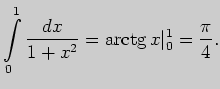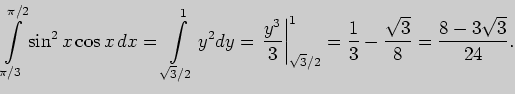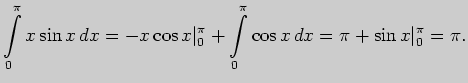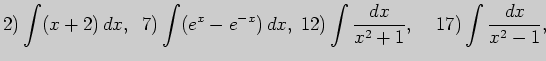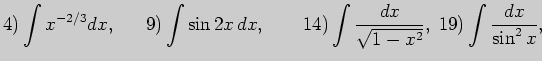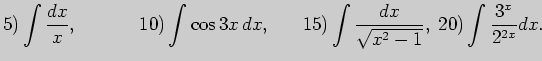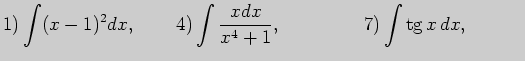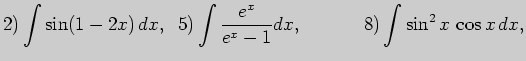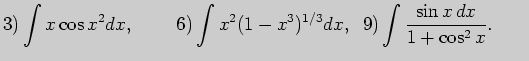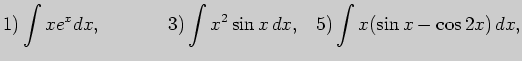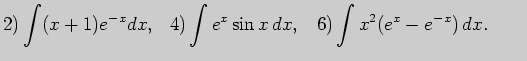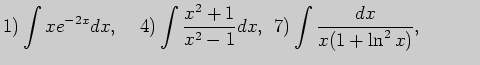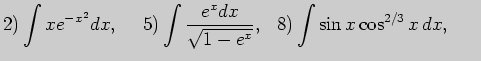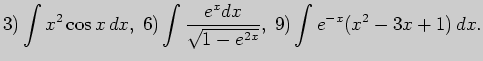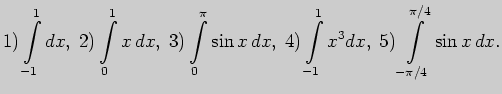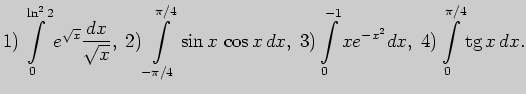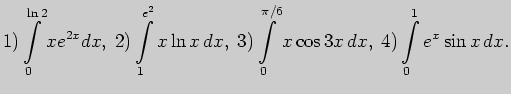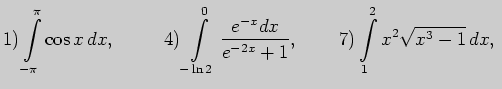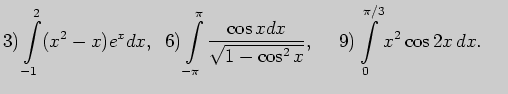Далее: Об этом документе ...
Вверх: II. Элементы математического анализа
Назад: 3. Производная и ее
Вопросы теории. Понятие неопределенного интеграла. Свойства
первообразных функции. Замена переменной и интегрирование
по частям. Задача о площади криволинейной
трапеции. Понятие и свойства определенного интеграла. Формула Ньютона -
Лейбница.
Образцы решения задач
Задача 1. Выполните интегрирование:
Решение. Первый интеграл вычисляется непосредственно:
Для вычисления второго интеграла сделаем замену переменной интегрирования:
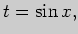
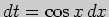 .
В третьем интеграле применим формулу интегрирования по частям,
выбрав
.
В третьем интеграле применим формулу интегрирования по частям,
выбрав
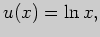
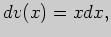 откуда
откуда
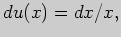
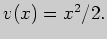 Задача 2. Выполните интегрирование:
Решение. Первый интеграл вычисляется непосредственным применением формулы
Ньютона - Лейбница:
Во втором интеграле сделаем замену переменной интегрирования
Задача 2. Выполните интегрирование:
Решение. Первый интеграл вычисляется непосредственным применением формулы
Ньютона - Лейбница:
Во втором интеграле сделаем замену переменной интегрирования
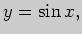

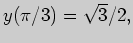
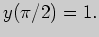 Третий интеграл вычислим "по частям", выбрав
Третий интеграл вычислим "по частям", выбрав 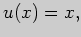
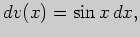 откуда
откуда 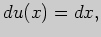
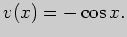 Задачи для самостоятельного решения
Задачи для самостоятельного решения
1. Укажите две различные первообразные функции 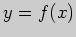 :
:
2. Выполните неопределенное интегрирование (непосредственно):
3. Выполните неопределенное интегрирование (заменой переменной):
4. Выполните неопределенное интегрирование (по частям):
5. Выполните неопределенное интегрирование, выбрав метод самостоятельно:
6. Выполните определенное интегрирование (непосредственно):
7. Выполните определенное интегрирование (заменой переменной):
8. Выполните определенное интегрирование (по частям):
9. Выполните определенное интегрирование, выбрав метод самостоятельно:
Далее: Об этом документе ...
Вверх: II. Элементы математического анализа
Назад: 3. Производная и ее
ЯГПУ, Центр информационных технологий обучения
27.03.2007