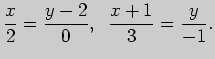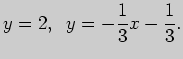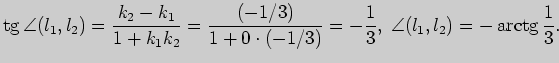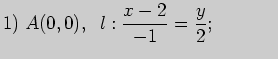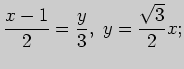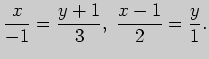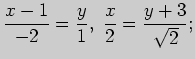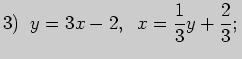Далее: 3. Системы линейных уравнений
Вверх: I. Элементы аналитической геометрии
Назад: 1. Векторная алгебра
Вопросы теории. Различные виды уравнения прямой на плоскости:
уравнение с угловым коэффициентом, общее уравнение, каноническое и
параметрические уравнения. Геометрический смысл коэффициентов, входящих в
уравнение каждого типа. Направляющий вектор и вектор нормали. Взаимное
расположение точки и прямой на плоскости. Угол между прямыми. Взаимное
расположение пары прямых. Условия параллельности и перпендикулярности прямых.
Образцы решения задач
Задача 1. Напишите параметрические уравнения прямой, проходящей через
точки 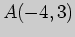 и
и 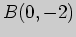 . Выясните, проходит ли эта прямая через начало
координат.
. Выясните, проходит ли эта прямая через начало
координат.
Решение. В качестве направляющего вектора 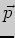 прямой можно взять
вектор
прямой можно взять
вектор 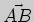 или любой коллинеарный ему вектор. Положим
или любой коллинеарный ему вектор. Положим
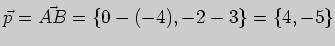 . В качестве точки, отвечающей
нулевому значению параметра
. В качестве точки, отвечающей
нулевому значению параметра 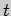 , можно выбрать любую из данных точек, например,
точку
, можно выбрать любую из данных точек, например,
точку 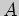 :
: 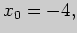
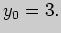 Подстановка этих данных в параметрические уравнения
Подстановка этих данных в параметрические уравнения
приводит к искомым уравнениям
Осталось проверить, удовлетворяют ли полученным уравнениям координаты (0,0)
данной точки.
Для этого положим в этих уравнениях 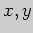 равными этим координатам и
вычислим значения параметра
равными этим координатам и
вычислим значения параметра 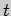 из каждого уравнения. Если значения
параметра, полученные из первого и второго уравнений, равны, то данная
точка принадлежит прямой, иначе - нет:
Итак,
из каждого уравнения. Если значения
параметра, полученные из первого и второго уравнений, равны, то данная
точка принадлежит прямой, иначе - нет:
Итак,
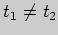 , прямая не проходит через начало координат.
, прямая не проходит через начало координат.
Задача 2. Для данных точки 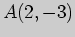 и прямой
и прямой
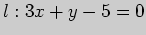
а) напишите уравнение прямой, проходящей через данную точку параллельно
данной прямой,
б) напишите уравнение прямой, проходящей через данную точку перпендикулярно
данной прямой.
Решение. а) Всякая прямая, параллельная прямой, задаваемой общим
уравнением
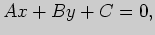 описывается уравнением
описывается уравнением
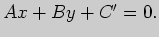 Поэтому искомая
прямая может быть задана уравнением
Поэтому искомая
прямая может быть задана уравнением 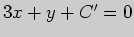 . Свободный член
. Свободный член 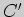 определим из условия, что точка
определим из условия, что точка 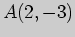 принадлежит данной прямой, т.е.
принадлежит данной прямой, т.е.
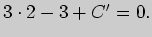 Отсюда
Отсюда 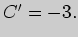 Итак, прямая, параллельная данной прямой и
проходящая через данную точку
Итак, прямая, параллельная данной прямой и
проходящая через данную точку 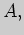 задается уравнением
задается уравнением 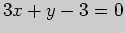 .
.
б) Вектор нормали к прямой, заданной общим уравнением 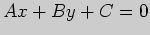 ,
коллинеарен вектору с координатами
,
коллинеарен вектору с координатами 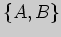 , поэтому вектор нормали
к прямой
, поэтому вектор нормали
к прямой 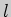 может быть выбран в виде
может быть выбран в виде
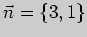 . Тогда
вектор нормали
. Тогда
вектор нормали 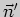 к искомой прямой ортогонален вектору
к искомой прямой ортогонален вектору 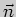 .
В качестве вектора
.
В качестве вектора 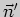 можно выбрать вектор с координатами
можно выбрать вектор с координатами 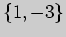 (проверьте!). Тогда искомое уравнение имеет вид
(проверьте!). Тогда искомое уравнение имеет вид 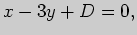 причем прямая
проходит через точку
причем прямая
проходит через точку 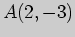 . Подставляя координаты точки
. Подставляя координаты точки 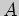 в уравнение,
находим
в уравнение,
находим 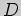 :
Таким образом, прямая задается уравнением
:
Таким образом, прямая задается уравнением
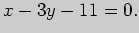
Задача 3. Выясните взаимное расположение прямых, заданных уравнениями
Если прямые пересекаются, найдите координаты точки пересечения и угол,
образуемый прямыми в том порядке, в котором они указаны.
Решение. Прямые заданы каноническими уравнениями, поэтому вывод об их
взаимном расположении может быть сделан из анализа направляющих векторов;
если векторы коллинеарны, то прямые параллельны либо совпадают, в противном
случае прямые пересекаются. Направляющий вектор первой прямой равен
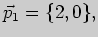 направляющий вектор второй прямой -
направляющий вектор второй прямой -
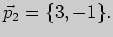 Векторы неколлинеарны, значит, прямые пересекаются. Вычислим координаты их
точки пересечения
Векторы неколлинеарны, значит, прямые пересекаются. Вычислим координаты их
точки пересечения
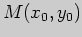 . Для этого перепишем уравнения прямых в
форме с угловым коэффициентом:
Решая образованную ими систему, находим:
. Для этого перепишем уравнения прямых в
форме с угловым коэффициентом:
Решая образованную ими систему, находим: 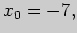
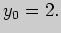 Теперь
вычислим угол
Теперь
вычислим угол
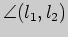 , образованный прямыми:
, образованный прямыми:
Задачи для самостоятельного решения
1. Напишите уравнение прямой, проходящей через две данные точки, в следующих
формах:
а) с угловым коэффициентом (если возможно),
б) общее,
в) каноническое,
г) параметрические.
Укажите направляющий вектор этой прямой. Однозначно ли он определен?
Укажите вектор нормали к этой прямой. Единственен ли он?
1) 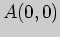 , , 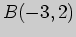 ; ; |
3) 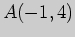 , , 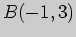 ; ; |
2) 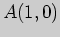 , , 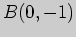 ; ; |
4) 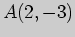 , , 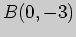 . . |
2. Для данных точки и вектора задайте уравнениями пару прямых, проходящих
через данную точку, из которых одна параллельна данному вектору, а другая
перпендикулярна ему.
1) 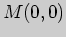 , ,
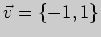 ; ; |
3) 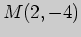 , ,
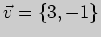 ; ; |
2) 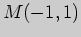 , ,
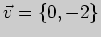 ; ; |
4) 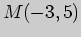 , ,
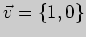 . . |
3. Для данных точки и прямой
а) выясните, лежит ли точка на прямой,
б) напишите уравнение прямой, проходящей через данную точку параллельно
данной прямой,
в) напишите уравнение прямой, проходящей через данную точку перпендикулярно
данной прямой.
Уравнения прямых напишите в том же виде, в котором написано уравнение данной
прямой.
4. Вычислите угол между прямыми.
5. Выясните взаимное расположение пары прямых. Если прямые
пересекаются, найдите координаты точки пересечения.
Далее: 3. Системы линейных уравнений
Вверх: I. Элементы аналитической геометрии
Назад: 1. Векторная алгебра
ЯГПУ, Центр информационных технологий обучения
27.03.2007
![]() и
и ![]() . Выясните, проходит ли эта прямая через начало
координат.
. Выясните, проходит ли эта прямая через начало
координат.
![]() прямой можно взять
вектор
прямой можно взять
вектор ![]() или любой коллинеарный ему вектор. Положим
или любой коллинеарный ему вектор. Положим
![]() . В качестве точки, отвечающей
нулевому значению параметра
. В качестве точки, отвечающей
нулевому значению параметра ![]() , можно выбрать любую из данных точек, например,
точку
, можно выбрать любую из данных точек, например,
точку ![]() :
: ![]()
![]() Подстановка этих данных в параметрические уравнения
Подстановка этих данных в параметрические уравнения