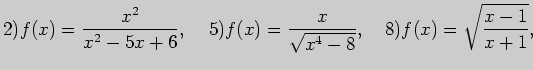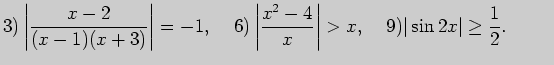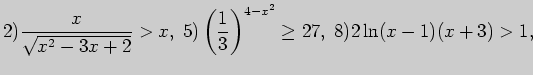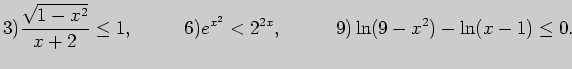Далее: 2. Предел. Непрерывность
Вверх: II. Элементы математического анализа
Назад: II. Элементы математического анализа
Вопросы теории. Элементы теории множеств: понятие множества,
подмножества, объединения и пересечения подмножеств. Диаграммы
Эйлера - Венна.
Подмножества числовой прямой
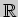 . Понятие числовой функции. Область определения
и область значений функции. Монотонность функции. Основные элементарные
функции, их свойства и графики. Операции над функциями. Класс элементарных
функций. Модуль действительного числа. Свойства модуля.
. Понятие числовой функции. Область определения
и область значений функции. Монотонность функции. Основные элементарные
функции, их свойства и графики. Операции над функциями. Класс элементарных
функций. Модуль действительного числа. Свойства модуля.
Образцы решения задач
Задача 1. Постройте объединение 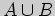 , пересечение
, пересечение 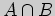 и
дополнения
и
дополнения
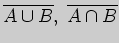 для подмножеств
для подмножеств
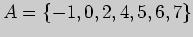 и
и
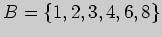 данного множества
данного множества
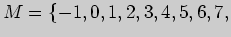
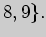
Решение. Согласно определению, объединение 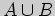 подмножеств
подмножеств 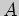 и
и
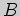 множества
множества 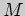 состоит из тех его элементов, которые принадлежат
хотя бы одному из подмножеств
состоит из тех его элементов, которые принадлежат
хотя бы одному из подмножеств 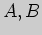 . Пересечение
. Пересечение 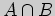 подмножеств
подмножеств 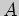 и
и
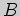 множества
множества 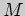 состоит из тех его элементов, которые принадлежат обоим
подмножествам
состоит из тех его элементов, которые принадлежат обоим
подмножествам 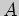 и
и 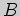 . Наконец, дополнение
. Наконец, дополнение 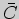 к подмножеству
к подмножеству 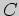 множества
множества 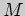 состоит из тех элементов множества
состоит из тех элементов множества 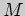 , которые
не принадлежат
, которые
не принадлежат 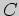 . Поэтому можно выписать такую таблицу
. Поэтому можно выписать такую таблицу
Задача 2. Вычислите область определения функции
Решение. Данная функция определена при тех значениях
независимой переменной 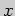 , при которых имеют смысл все входящие в нее
выражения. Значение рациональной дроби не определено в тех точках числовой
прямой, в которых знаменатель обращается в нуль, т.е. при
, при которых имеют смысл все входящие в нее
выражения. Значение рациональной дроби не определено в тех точках числовой
прямой, в которых знаменатель обращается в нуль, т.е. при 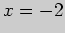 и при
и при 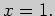 Таким образом, рациональная дробь определена на множестве
Таким образом, рациональная дробь определена на множестве
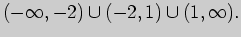 Логарифм определен при строго положительных значениях
аргумента, т.е. при
Логарифм определен при строго положительных значениях
аргумента, т.е. при
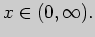 Пересечение указанных множеств дает
искомую область определения
Пересечение указанных множеств дает
искомую область определения
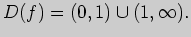
Задача 3. Решите неравенство
Решение. Приведем все выражения, входящие в неравенство, к общему
основанию 2:
Показательная функция
определена на всей числовой прямой. Показательная функция по
основанию 2 - монотонно возрастающая, поэтому полученное неравенство
равносильно неравенству
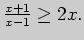 Перенос выражения
Перенос выражения 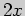 в левую часть и приведение к общему знаменателю приводят к выражению
Полученное неравенство нетрудно
решить методом интервалов:
в левую часть и приведение к общему знаменателю приводят к выражению
Полученное неравенство нетрудно
решить методом интервалов:
Задачи для самостоятельного решения
1. Постройте объединение 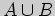 , пересечение
, пересечение 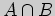 и дополнения
и дополнения
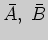 подмножеств
подмножеств 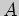 и
и 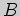 данного множества
данного множества 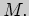
1)
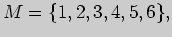
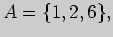
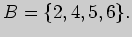
2)
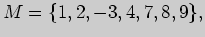
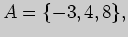
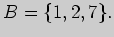
3)
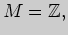
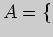 все натуральные числа
все натуральные числа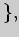
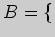 все четные
числа
все четные
числа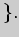
4)
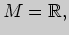
![$ A=[-1,2],$](img302.png)
![$ B=[-2,0].$](img303.png)
5)
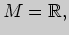
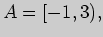
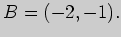
6)
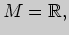
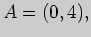
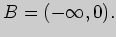
2. Пользуясь диаграммами Эйлера - Венна, проверьте истинность равенств
1)
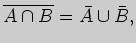 2)
2)
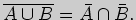
3. Найдите область определения функции
4. Решите уравнения и неравенства с модулем
5. Решите иррациональные, показательные и логарифмические уравнения
и неравенства.
Далее: 2. Предел. Непрерывность
Вверх: II. Элементы математического анализа
Назад: II. Элементы математического анализа
ЯГПУ, Центр информационных технологий обучения
27.03.2007
![]() . Понятие числовой функции. Область определения
и область значений функции. Монотонность функции. Основные элементарные
функции, их свойства и графики. Операции над функциями. Класс элементарных
функций. Модуль действительного числа. Свойства модуля.
. Понятие числовой функции. Область определения
и область значений функции. Монотонность функции. Основные элементарные
функции, их свойства и графики. Операции над функциями. Класс элементарных
функций. Модуль действительного числа. Свойства модуля.
![]() , пересечение
, пересечение ![]() и
дополнения
и
дополнения
![]() для подмножеств
для подмножеств
![]() и
и
![]() данного множества
данного множества
![]()
![]()
![]() подмножеств
подмножеств ![]() и
и
![]() множества
множества ![]() состоит из тех его элементов, которые принадлежат
хотя бы одному из подмножеств
состоит из тех его элементов, которые принадлежат
хотя бы одному из подмножеств ![]() . Пересечение
. Пересечение ![]() подмножеств
подмножеств ![]() и
и
![]() множества
множества ![]() состоит из тех его элементов, которые принадлежат обоим
подмножествам
состоит из тех его элементов, которые принадлежат обоим
подмножествам ![]() и
и ![]() . Наконец, дополнение
. Наконец, дополнение ![]() к подмножеству
к подмножеству ![]() множества
множества ![]() состоит из тех элементов множества
состоит из тех элементов множества ![]() , которые
не принадлежат
, которые
не принадлежат ![]() . Поэтому можно выписать такую таблицу
. Поэтому можно выписать такую таблицу
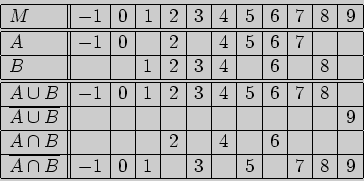
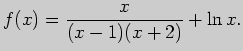
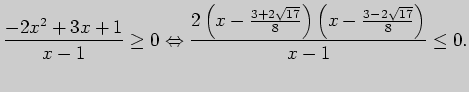
![$\displaystyle x\in \left( -\infty,\frac{3-2\sqrt{17}}{8}\right] \cup
\left( 1,\frac{3+2\sqrt{17}}{8}\right].
$](img287.png)