Число ![]() называется пределом числовой
последовательности
называется пределом числовой
последовательности ![]() , если для любого
, если для любого
![]() существует такое натуральное
число
существует такое натуральное
число ![]() , что для любого
, что для любого
![]() верно
неравенство:
верно
неравенство: ![]() .
.
Рассмотрим числовые последовательности вида:
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
целые числа, причем
-
целые числа, причем
![]() и
и ![]() .
.
Пределом числовых последовательностей является отношение:
Необходимо осуществить приближенные вычисления значений минимальных
номеров
![]() числовых последовательностей
числовых последовательностей
![]() по
заданным
по
заданным ![]() ,
таких, что для всех членов числовых
последовательностей со значениями номеров
,
таких, что для всех членов числовых
последовательностей со значениями номеров
![]() выполняется
неравенство
выполняется
неравенство ![]() в
соответствии с
различными условиями варьирования значений исходных данных.
в
соответствии с
различными условиями варьирования значений исходных данных.
Рассмотрим функцию
![]() :
:
От рассмотрения функции
![]() перейдем к
рассмотрению функции
перейдем к
рассмотрению функции ![]() (экстраполируя
(экстраполируя
![]() на положительную
на положительную ![]() , так как график функции
, так как график функции
![]() отличается от
графика функции
отличается от
графика функции ![]() (в
смысле выяснения особенностей, т.е. действительных точек разрыва и
экстремума) только появлением дополнительной действительной угловой
точки
графика на оси абсцисс:
(в
смысле выяснения особенностей, т.е. действительных точек разрыва и
экстремума) только появлением дополнительной действительной угловой
точки
графика на оси абсцисс:
Для определения действительных точек разрыва функции
![]() , то
есть действительных точек несуществования функции
, то
есть действительных точек несуществования функции
![]() ,
необходимо решить уравнение
,
необходимо решить уравнение
![]() (
(![]() в
силу
существования предела последовательности).
в
силу
существования предела последовательности).
В силу решения квадратного уравнения возможны следующие варианты
наличия у
функции ![]() действительных точек разрыва (
действительных точек разрыва (
![]() :
:
Если ![]() , то функция
, то функция
![]() не имеет действительных
точек разрыва и непрерывна на всей числовой оси.
не имеет действительных
точек разрыва и непрерывна на всей числовой оси.
Если ![]() , то функция
, то функция
![]() имеет одну действительную
точку разрыва со следующим значением абсциссы:
имеет одну действительную
точку разрыва со следующим значением абсциссы:
![]() .
.
Если ![]() , то функция
, то функция
![]() имеет две действительные
точки разрыва со следующими значениями абсцисс:
имеет две действительные
точки разрыва со следующими значениями абсцисс:
Для определения действительных точек экстремума функции
![]() ,
то есть действительных точек, в которых данная функция имеет максимум
или
минимум, необходимо решить уравнение
,
то есть действительных точек, в которых данная функция имеет максимум
или
минимум, необходимо решить уравнение
![]() и выявить
характер действительных критических точек.
и выявить
характер действительных критических точек.
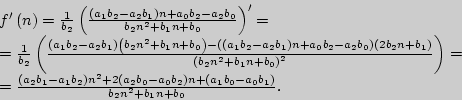
В силу решения квадратного уравнения, левая часть которого представлена
в числителе, а именно,
![]() и
влияния знаменателя возможны следующие варианты наличия у функции
и
влияния знаменателя возможны следующие варианты наличия у функции
![]() действительных критических точек
действительных критических точек
![]() ,
причем
,
причем ![]() в силу существования предела последовательности:
в силу существования предела последовательности:
Если ![]() , то функция
, то функция
![]() не имеет действительных
критических точек.
не имеет действительных
критических точек.
Если ![]() , то функция
, то функция
![]() должна иметь одну
действительную критическую точку со следующим значением абсциссы:
должна иметь одну
действительную критическую точку со следующим значением абсциссы:
![]() .
.
Действительно, если ![]() , то есть
, то есть
![]() ,
и
,
и
![]() , то
получим:
, то
получим:
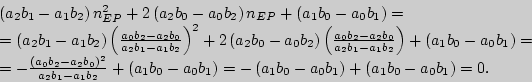
Однако при соблюдении предлагаемых договоренностей имеем:
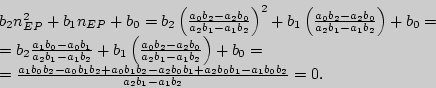
Таким образом, если ![]() , то
, то
![]() ,
что противоречит условию существования производной функции
,
что противоречит условию существования производной функции
![]() , то есть при данных условиях функция
, то есть при данных условиях функция
![]() не имеет
действительных критических точек.
не имеет
действительных критических точек.
Если ![]() , то функция
, то функция
![]() должна иметь две
действительные критические точки со следующими значениями абсцисс:
должна иметь две
действительные критические точки со следующими значениями абсцисс:
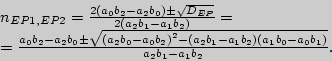
Если при
![]() получим, что
получим, что ![]() , то функция
, то функция
![]() имеет
только одну действительную критическую точку со следующим значением
абсциссы:
имеет
только одну действительную критическую точку со следующим значением
абсциссы:

Если при
![]() получим, что
получим, что ![]() , то функция
, то функция
![]() имеет
только одну действительную критическую точку со следующим значением
абсциссы:
имеет
только одну действительную критическую точку со следующим значением
абсциссы:
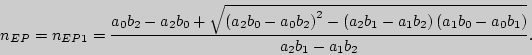
Если при
![]() получим, что
получим, что
![]() , то
функция
, то
функция ![]() имеет две действительные критические точки со следующими значениями
абсцисс:
имеет две действительные критические точки со следующими значениями
абсцисс:
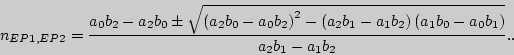
Нахождение действительной угловой точки осуществляется в результате
анализа
функции ![]() :
:
Действительная угловая точка означает пересечение графика функции
![]() с осью абсцисс, то
есть точку, в которой график
функции резко меняет направление в силу зеркального отображения
отрицательных областей графика функции
с осью абсцисс, то
есть точку, в которой график
функции резко меняет направление в силу зеркального отображения
отрицательных областей графика функции
![]() относительно оси
абсцисс.
относительно оси
абсцисс.
Для определения действительной угловой точки функции
![]() , то есть точки, в
которой функции
, то есть точки, в
которой функции ![]() и
и
![]() пересекают ось абсцисс, необходимо
решить уравнение
пересекают ось абсцисс, необходимо
решить уравнение ![]() :
:
В силу решения линейного уравнения, левая часть которого представлена в
числителе, а именно,
![]() и
влияния знаменателя возможны следующие варианты наличия у функции
и
влияния знаменателя возможны следующие варианты наличия у функции
![]() действительных
угловых точек, причем
действительных
угловых точек, причем
![]() в силу существования предела
последовательности:
в силу существования предела
последовательности:
Если ![]() , то функция
, то функция
![]() не имеет
действительной угловой точки.
не имеет
действительной угловой точки.
Если ![]() , то функция
, то функция
![]() должна иметь одну
действительную угловую точку со следующим
значением абсциссы:
должна иметь одну
действительную угловую точку со следующим
значением абсциссы:
![]() .
.
Если при
![]() получим,
что
получим,
что ![]() , то функция
, то функция
![]() не имеет
действительной угловой точки;
не имеет
действительной угловой точки;
Если при
![]() получим,
что
получим,
что ![]() , то функция
, то функция
![]() имеет одну
действительную угловую точку со следующим
значением абсциссы:
имеет одну
действительную угловую точку со следующим
значением абсциссы:
![]() .
.
После нахождения действительных точек разрыва (![]() ,
,![]() или
или
![]() , точек экстремума (
, точек экстремума (![]() ,
,![]() или
или ![]() и угловой
точки (
и угловой
точки (![]() для функции
для функции
![]() определим
отрезок
определим
отрезок ![]() с условием
с условием
![]() , на
котором следует осуществлять нахождение значения минимального номера
, на
котором следует осуществлять нахождение значения минимального номера
![]() , где
, где ![]() -
минимальный номер,
теоретически найденный
аналитическим методом, а значение
-
минимальный номер,
теоретически найденный
аналитическим методом, а значение ![]() определяется из
выражения
определяется из
выражения
![]() ,
при этом для дальнейших расчетов в
случаях наличия дробных частей значения граничных номеров следует
округлять
до больших ближайших целых чисел.
,
при этом для дальнейших расчетов в
случаях наличия дробных частей значения граничных номеров следует
округлять
до больших ближайших целых чисел.
Порядок нахождения значения ![]() в силу
особенностей
функции
в силу
особенностей
функции ![]() состоит из
следующих
этапов:
состоит из
следующих
этапов:
При отсутствии у функции
![]() действительных
точек разрыва
действительных
точек разрыва ![]() ;
;
При наличии у функции
![]() одной
действительной точки разрыва
одной
действительной точки разрыва ![]() ;
;
При наличии у функции
![]() двух
действительных точек разрыва если
двух
действительных точек разрыва если ![]() , то
, то ![]() , если
, если
![]() , то
, то ![]() ;
;
При отсутствии у функции
![]() действительных
точек экстремума
действительных
точек экстремума ![]() ;
;
При наличии у функции
![]() одной
действительной точки экстремума если
одной
действительной точки экстремума если
![]() ,
то
,
то ![]() ,
если
,
если
![]() ,
то
,
то ![]() ;
;
При наличии у функции
![]() двух
действительных точек экстремума если
двух
действительных точек экстремума если
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() ;
;
При наличии у функции
![]() двух
действительных точек экстремума если
двух
действительных точек экстремума если
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() ;
;
При наличии у функции
![]() двух
действительных точек экстремума если
двух
действительных точек экстремума если
![]() , то
, то
![]() , если
, если
![]() , то
, то
![]() ;
;
При отсутствии у функции
![]() действительной
угловой точки
действительной
угловой точки ![]() ;
;
При наличии у функции
![]() одной
действительной угловой точки
одной
действительной угловой точки ![]() ;
;
В качестве ![]() выбирается округленное до
большего ближайшего целого
числа максимальное из значений
выбирается округленное до
большего ближайшего целого
числа максимальное из значений ![]() ,
, ![]() и
и ![]() .
.
Рассмотрим логические основы реализации методов золотой пропорции,
Фибоначчи, дихотомии для выполнения приближенных вычислений значений
пределов числовых последовательностей вида
![]() (для
(для
![]() ,
, ![]() ,
, ![]() ,
,
![]() на
основе
расчетов значений минимальных номеров
на
основе
расчетов значений минимальных номеров ![]() в
зависимости от
различных значений
в
зависимости от
различных значений ![]() ,
, ![]() и
и ![]() , заложенных в
программу "MINNESQS".
, заложенных в
программу "MINNESQS".
Суть золотой пропорции, изображенной на рис. 1, состоит в следующем: если разделить отрезок С на отрезки А и В таким образом, что это будет отражать золотую пропорцию, то А, деленное на В, будет равно С, деленному на А.
Символьная запись:
![]() .
.
Действительно, пусть ![]() .
.
Так как ![]() или
или
![]() , то
получим квадратное уравнение:
, то
получим квадратное уравнение:
Положительный действительный корень квадратного уравнения:
По аналогии с пропорцией назовем число ![]() золотым.
золотым.
Одно из общеизвестных алгебраических свойств золотого числа
заключается в
следующем: золотое число, возведенное в степень с натуральным
показателем,
равно сумме двух золотых чисел, возведенных в две предшествующие
степени:
![]() .
.
Действительно, так как
![]() , то
, то
![]() или
или
![]() ,
откуда
,
откуда
![]() .
.
Поскольку
![]() ,
то
,
то
![]() ,
откуда можно получить следующие
соотношения:
,
откуда можно получить следующие
соотношения:
В данной лабораторной работе метод золотой пропорции ("METHOD OF GOLD PROPORTION") имеет следующую реализацию:
Итерация с индексом ![]() :
:
На искомом отрезке
![]() при соблюдении условий
при соблюдении условий
![]() и
и
![]() (по умолчанию
значения
(по умолчанию
значения ![]() и
и ![]() являются
целыми
числами) выбираются точки с
абсциссами
являются
целыми
числами) выбираются точки с
абсциссами ![]() и
и ![]() ,
исходя из неравенств
,
исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами золотой пропорции согласно следующим
соотношениям:
,
в
соответствии с принципами золотой пропорции согласно следующим
соотношениям:
При наличии положительных дробных частей значения ![]() и
и
![]() округляются до ближайших больших целых чисел.
округляются до ближайших больших целых чисел.
Если достигнута истинность выражения
![]() , то итерации
прекращаются, количество шагов итераций
, то итерации
прекращаются, количество шагов итераций
![]() , и в
качестве минимального номера
, и в
качестве минимального номера ![]() выбирается
выбирается
![]() в силу неравенства
в силу неравенства
![]() .
.
Если ![]() , то осуществляется переход к
следующей
итерации.
, то осуществляется переход к
следующей
итерации.
Итерация с индексом ![]() :
:
Если
![]() ,
то
,
то ![]() ,
,
![]() ,
,
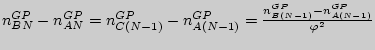 ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
Если
![]() и
и
![]() ,
то
,
то ![]() ,
,
![]() ,
,
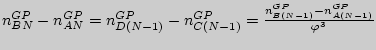 ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
Если
![]() ,
то
,
то ![]() ,
,
![]() ,
,
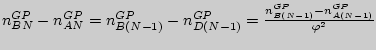 ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
На отрезке
![]() при соблюдении
условий
при соблюдении
условий ![]() и
и
![]() выбираются точки с абсциссами
выбираются точки с абсциссами ![]() и
и ![]() ,
исходя из неравенств
,
исходя из неравенств
![]() и
и
![]() ,
в
соответствии с
принципами золотой пропорции согласно следующим соотношениям:
,
в
соответствии с
принципами золотой пропорции согласно следующим соотношениям:
При наличии положительных дробных частей значения ![]() и
и
![]() округляются до ближайших больших целых чисел.
округляются до ближайших больших целых чисел.
Если достигнута истинность выражения
![]() , то
итерации прекращаются, количество шагов итераций
, то
итерации прекращаются, количество шагов итераций
![]() ,
и в качестве минимального номера
,
и в качестве минимального номера
![]() выбирается
выбирается
![]() в силу неравенства
в силу неравенства
![]() .
.
Если ![]() , то осуществляется переход к
следующей итерации.
, то осуществляется переход к
следующей итерации.
Последовательность чисел Фибоначчи (открыта Леонардо Фибоначчи) отличается от других последовательностей чисел тем, что каждый ее член, начиная со второго по индексу, равен сумме двух предыдущих (с добавлением нулевого члена последовательности): 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее.
Действительно: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , то есть
, то есть
![]() , где
, где ![]() ,
, ![]() и
и ![]() члены последовательности
Фибоначчи с индексами
члены последовательности
Фибоначчи с индексами ![]() ,
, ![]() и
и
![]() соответственно.
соответственно.
Интересно отметить, что отношение значений соседних членов данной
последовательности, начиная с больших номеров (при
![]() ,
приближается к золотому числу, то есть
,
приближается к золотому числу, то есть ![]() :
:
где ![]() и
и ![]() члены
последовательности Фибоначчи с
индексами
члены
последовательности Фибоначчи с
индексами ![]() и
и ![]() соответственно.
соответственно.
Для золотых чисел, возведенных в определенных степенях
(геометрическая
прогрессия со значениями начального члена и знаменателя, равными ![]() ), как и
для последовательности чисел Фибоначчи, справедливо общее правило о
том, что
значение каждого члена любой из этих последовательностей равно сумме
значений двух предыдущих членов:
), как и
для последовательности чисел Фибоначчи, справедливо общее правило о
том, что
значение каждого члена любой из этих последовательностей равно сумме
значений двух предыдущих членов:
Формула для геометрической прогрессии золотых чисел:
![]() ,
где
,
где ![]() ,
, ![]() и
и ![]() - показатели
степеней для золотого числа
- показатели
степеней для золотого числа ![]() ;
;
Формула для последовательности чисел Фибоначчи:
![]() , где
, где ![]() ,
, ![]() и
и ![]() члены
последовательности Фибоначчи с индексами
члены
последовательности Фибоначчи с индексами ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
Поскольку ![]() , то
, то
![]() ,
откуда можно получить следующие соотношения:
,
откуда можно получить следующие соотношения:
Взаимосвязь между золотым числом и числами Фибоначчи выражается
следующим
соотношением:
![]() .
.
Докажем утверждение методом последовательного перебора:
В данной лабораторной работе метод Фибоначчи ("METHOD OF FIBONACHCHI") имеет следующую реализацию:
Итерация с индексом ![]() :
:
Осуществляется ввод значения индекса последнего члена ряда Фибоначчи
для его
построения, то есть ![]() .
.
Осуществляется построение заданного ряда Фибоначчи, начиная с
нулевого
индекса и заканчивая индексом ![]() .
.
На искомом отрезке
![]() при соблюдении условий
при соблюдении условий
![]() и
и
![]() (по умолчанию
значения
(по умолчанию
значения ![]() и
и ![]() являются
целыми
числами) выбираются точки с
абсциссами
являются
целыми
числами) выбираются точки с
абсциссами ![]() и
и ![]() ,
исходя из неравенств
,
исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами последовательности Фибоначчи согласно
следующим
соотношениям:
,
в
соответствии с принципами последовательности Фибоначчи согласно
следующим
соотношениям:
При наличии положительных дробных частей значения ![]() и
и ![]() округляются до ближайших больших целых чисел.
округляются до ближайших больших целых чисел.
Если достигнута истинность выражения
![]() , то итерации
прекращаются, количество шагов итераций
, то итерации
прекращаются, количество шагов итераций
![]() , и в качестве
минимального номера
, и в качестве
минимального номера ![]() выбирается
выбирается
![]() в силу неравенства
в силу неравенства
![]() .
.
Если ![]() , то осуществляется переход к
следующей
итерации.
, то осуществляется переход к
следующей
итерации.
Итерация с индексом ![]() :
:
Если
![]() ,
то
,
то ![]() ,
,
![]() ,
,
![]() ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
Если
![]() и
и
![]() ,
то
,
то ![]() ,
,
![]() ,
,
![]() ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
Если
![]() ,
то
,
то ![]() ,
,
![]() ,
,
![]() ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
На отрезке ![]() при соблюдении
условий
при соблюдении
условий
![]() и
и
![]() выбираются точки
с абсциссами
выбираются точки
с абсциссами ![]() и
и ![]() ,
исходя из неравенств
,
исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами последовательности Фибоначчи согласно
следующим соотношениям:
,
в
соответствии с принципами последовательности Фибоначчи согласно
следующим соотношениям:
При наличии положительных дробных частей значения ![]() и
и ![]() округляются до ближайших больших целых чисел.
округляются до ближайших больших целых чисел.
Если достигнута истинность выражения
![]() , то итерации
прекращаются, количество шагов итераций
, то итерации
прекращаются, количество шагов итераций
![]() , и в качестве
минимального номера
, и в качестве
минимального номера ![]() выбирается
выбирается
![]() в силу неравенства
в силу неравенства
![]() .
.
Если ![]() , то осуществляется переход к
следующей
итерации.
, то осуществляется переход к
следующей
итерации.
Стоит отметить, что при достаточно большом значении начального
индекса ![]() соответствующие отрезки, полученные методами золотой пропорции и
Фибоначчи,
будут иметь незначительные отличия, что влечет за собой приблизительно
равную эффективность обоих методов.
соответствующие отрезки, полученные методами золотой пропорции и
Фибоначчи,
будут иметь незначительные отличия, что влечет за собой приблизительно
равную эффективность обоих методов.
Суть дихотомии или половинного деления состоит в следующем: если
разделить
отрезок C на отрезки A и B таким образом, что это будет отражать
дихотомию,
то C, деленное на A, будет равно C, деленному на B, то есть A равно B:
![]() или
или ![]() .
.
Таким образом, при наличии исходного отрезка
![]() полученный в результате
полученный в результате ![]() -го деления отрезок
-го деления отрезок
![]() связан с исходным соотношением
связан с исходным соотношением
![]() .
.
В данной лабораторной работе метод дихотомии ("METHOD OF DICHOTOMY") имеет следующую реализацию:
Итерация с индексом ![]() :
:
Осуществляется ввод значения расстояния, откладываемого симметрично
относительно середины отрезка, для установки точек, то есть ![]() .
.
Если ![]() , то на искомом отрезке
, то на искомом отрезке
![]() при соблюдении условий
при соблюдении условий
![]() и
и
![]() (по умолчанию значения
(по умолчанию значения ![]() и
и ![]() являются
целыми числами) выбирается точка с абсциссой
являются
целыми числами) выбирается точка с абсциссой
![]() , исходя
из неравенств
, исходя
из неравенств ![]() и
и
![]() ,
в
соответствии с принципами дихотомии согласно следующему
соотношению:
,
в
соответствии с принципами дихотомии согласно следующему
соотношению:
Если ![]() , то на искомом отрезке
, то на искомом отрезке
![]() при соблюдении условий
при соблюдении условий
![]() и
и
![]() (по
умолчанию значения
(по
умолчанию значения ![]() и
и
![]() являются целыми числами) выбираются точки с
абсциссами
являются целыми числами) выбираются точки с
абсциссами ![]() и
и ![]() , исходя из неравенств
, исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами дихотомии
согласно следующим соотношениям:
,
в
соответствии с принципами дихотомии
согласно следующим соотношениям:
Если ![]() , то на искомом отрезке
, то на искомом отрезке
![]() при соблюдении условий
при соблюдении условий
![]() и
и
![]() (по умолчанию значения
(по умолчанию значения ![]() и
и ![]() являются целыми числами) выбираются точки с абсциссами
являются целыми числами) выбираются точки с абсциссами ![]() и
и
![]() , исходя из неравенств
, исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами дихотомии
согласно следующим соотношениям:
,
в
соответствии с принципами дихотомии
согласно следующим соотношениям:
При наличии положительных дробных частей значения ![]() и
и ![]() округляются до ближайших больших целых чисел.
округляются до ближайших больших целых чисел.
Если достигнута истинность выражения
![]() , то итерации
прекращаются, количество шагов итераций
, то итерации
прекращаются, количество шагов итераций
![]() , и в качестве
минимального номера
, и в качестве
минимального номера ![]() выбирается
выбирается
![]() в силу неравенства
в силу неравенства
![]() .
.
Если ![]() , то осуществляется переход к
следующей
итерации.
, то осуществляется переход к
следующей
итерации.
Итерация с индексом "N" ![]() :
:
Если
![]() ,
то
,
то ![]() ,
,
![]() ,
,
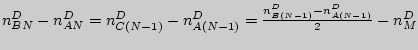 ,
и
получаем
отрезок
,
и
получаем
отрезок
![]() .
.
Если
![]() и
и
![]() ,
то
,
то ![]() ,
,
![]() ,
,
![]() ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
Если
![]() ,
то
,
то ![]() ,
,
![]() ,
,
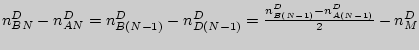 ,
и
получаем отрезок
,
и
получаем отрезок
![]() .
.
Если ![]() , то на отрезке
, то на отрезке
![]() при соблюдении
условий
при соблюдении
условий ![]() и
и
![]() выбирается точка с абсциссой
выбирается точка с абсциссой ![]() ,
исходя из неравенств
,
исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами дихотомии
согласно следующему соотношению:
,
в
соответствии с принципами дихотомии
согласно следующему соотношению:
Если ![]() , то на отрезке
, то на отрезке
![]() при соблюдении
условий
при соблюдении
условий ![]() и
и
![]() выбираются точки с абсциссами
выбираются точки с абсциссами ![]() и
и
![]() , исходя из неравенств
, исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами
дихотомии согласно следующим соотношениям:
,
в
соответствии с принципами
дихотомии согласно следующим соотношениям:
Если ![]() , то на отрезке
, то на отрезке
![]() при соблюдении
условий
при соблюдении
условий ![]() и
и
![]() выбираются точки с абсциссами
выбираются точки с абсциссами ![]() и
и
![]() , исходя из неравенств
, исходя из неравенств
![]() и
и
![]() ,
в
соответствии с принципами
дихотомии согласно следующим соотношениям:
,
в
соответствии с принципами
дихотомии согласно следующим соотношениям:
При наличии положительных дробных частей значения ![]() и
и ![]() округляются до ближайших больших целых чисел.
округляются до ближайших больших целых чисел.
Если достигнута истинность выражения
![]() , то итерации
прекращаются, количество шагов итераций
, то итерации
прекращаются, количество шагов итераций
![]() , и в качестве
минимального номера
, и в качестве
минимального номера ![]() выбирается
выбирается
![]() в силу неравенства
в силу неравенства
![]() .
.
Если ![]() , то осуществляется переход к
следующей
итерации.
, то осуществляется переход к
следующей
итерации.