План. Понятие топологического многообразия. Топологические многообразия с краем. Размерность топологического многообразия. Топологические подмногообразия размерностей 1 и 2 в вещественном евклидовом пространстве. Связная сумма топологических многообразий. Понятие дифференцируемого многообразия. Координатные функции и функции перехода. Примеры дифференцируемых многообразий.
Цель лекции - аксиоматизировать привычные черты кривых и
поверхностей и ввести топологический объект, локально устроенный
как евклидово пространство, а также подготовить методологическую
базу
для применения аппарата математического анализа в геометрии.
(Вещественным) топологическим многообразием (без края)
называется хаусдорфово топологическое пространство ![]() со
счетной базой, каждая точка которого обладает окрестностью,
гомеоморфной евклидову пространству
со
счетной базой, каждая точка которого обладает окрестностью,
гомеоморфной евклидову пространству
![]() . Число
. Число ![]() называется размерностью топологического многообразия
называется размерностью топологического многообразия ![]() .
.
Иногда удобнее использовать равносильную форму определения многообразия.
(Вещественным) топологическим многообразием (без
края) называется хаусдорфово топологическое
пространство ![]() со счетной базой, локально гомеоморфное
евклидову пространству
со счетной базой, локально гомеоморфное
евклидову пространству
![]() .
.
Важно, что топологические многообразия локально устроены как евклидовы пространства подходящей размерности. Однако можно построить топологические пространства, удовлетворяющие требованиям хаусдорфовости, локально гомеоморфные евклидову пространству, но не являющиеся многообразиями.
Простейший пример такого топологического пространства поставляет
объединение всех параллельных прямых на евклидовой плоскости,
заданных уравнениями ![]() где
где ![]() - иррациональное
число. Каждая из этих прямых удовлетворяет всем требованиям для
топологического многообразия. Объединение всех прямых с
иррациональными ординатами является хаусдорфовым
пространством, локально гомеоморфным числовой прямой
- иррациональное
число. Каждая из этих прямых удовлетворяет всем требованиям для
топологического многообразия. Объединение всех прямых с
иррациональными ординатами является хаусдорфовым
пространством, локально гомеоморфным числовой прямой
![]() . Однако на таком объединении невозможно ввести счетную
базу топологии. Чтобы убедиться в этом, зафиксируем на каждой из
прямых какую-нибудь счетную бесконечную базу. Очевидно,
объединение баз по всем прямым рассматриваемого набора
несчетно, так как его мощность не меньше мощности множества
иррациональных чисел.
. Однако на таком объединении невозможно ввести счетную
базу топологии. Чтобы убедиться в этом, зафиксируем на каждой из
прямых какую-нибудь счетную бесконечную базу. Очевидно,
объединение баз по всем прямым рассматриваемого набора
несчетно, так как его мощность не меньше мощности множества
иррациональных чисел.
Простейшими примерами топологических многообразий являются
числовая прямая с классической топологией, окружность и евклидова
плоскость. Более содержательный пример - двумерный тор
![]() . В лекции 2 рассмотрен пример локального
гомеоморфизма тора и евклидовой плоскости. Тор - хаусдорфово
пространство (рис. 7).
. В лекции 2 рассмотрен пример локального
гомеоморфизма тора и евклидовой плоскости. Тор - хаусдорфово
пространство (рис. 7).
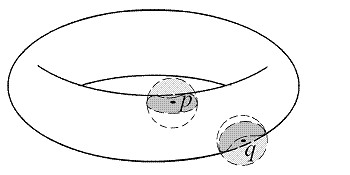
Для поверки этого факта рассмотрим две различные точки ![]() и
и ![]() тора, вложенного в трехмерное евклидово пространство
тора, вложенного в трехмерное евклидово пространство
![]() способом, описанным в лекции 2. Пространство
способом, описанным в лекции 2. Пространство
![]() , как известно
читателю, является метрическим. Поэтому в качестве
непересекающихся окрестностей точек
, как известно
читателю, является метрическим. Поэтому в качестве
непересекающихся окрестностей точек ![]() и
и ![]() в
пространстве
в
пространстве
![]() можно выбрать открытые шары достаточно малого
радиуса
можно выбрать открытые шары достаточно малого
радиуса ![]() . Тогда искомые непересекающиеся окрестности точек
. Тогда искомые непересекающиеся окрестности точек ![]() и
и ![]() на торе представлены его пересечениями с открытыми шарами.
на торе представлены его пересечениями с открытыми шарами.
Тор - топологическое пространство, допускающее счетную базу. Для ее построения зафиксируем счетную базу классической топологии в трехмерном евклидовом пространстве. Затем в качестве множеств, образующих базу на торе, возьмем пересечения тора и множеств базы топологии трехмерного пространства.
Упражнение. Пользуясь определением, убедитесь в том, что такие пересечения действительно образуют базу топологии тора.
Понятно, что построенная таким способом база топологии тора имеет мощность, не превосходящую мощность базы топологии трехмерного евклидова пространства, то есть является счетной. Таким образом, двумерный тор - хаусдорфово пространство со счетной базой, локально гомеоморфное евклидовой плоскости, то есть он является топологическим многообразием размерности два.
(Вещественным) топологическим многообразием c краем
называется хаусдорфово топологическое пространство ![]() со счетной базой, каждая точка
которого принадлежит одному из двух следующих классов:
со счетной базой, каждая точка
которого принадлежит одному из двух следующих классов:
1) класс точек, каждая из которых обладает окрестностью,
гомеоморфной евклидову пространству
![]() ;
;
2) класс точек, каждая из которых обладает окрестностью,
гомеоморфной полупространству
![]() евклидова пространства
евклидова пространства
![]() .
.
Точки первого класса называются внутренними точками
многообразия ![]() , точки второго класса - точками границы
или точками края. Число
, точки второго класса - точками границы
или точками края. Число ![]() называется размерностью
топологического многообразия
называется размерностью
топологического многообразия ![]() .
.
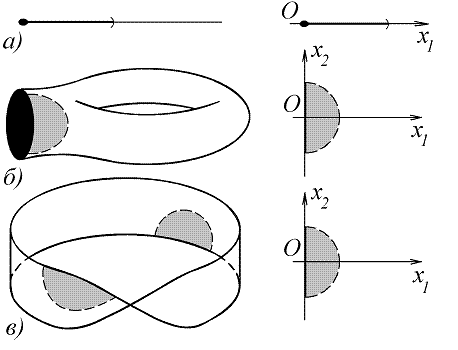
Примерами одномерных многообразий с краем служат отрезок и полупрямая, примерами двумерных - круг, тор с удаленным диском и лента Мебиуса (рис. 8). Границы трех последних многообразий гомеоморфны окружности, в то время как сами многообразия негомеоморфны.
Для конструирования топологических многообразий часто используется
операция приклеивания, заключающаяся в следующем. Пусть ![]() и
и ![]() - топологические многообразия,
- топологические многообразия,
![]() ,
,
![]() - подмножества, причем
- подмножества, причем ![]() гомеоморфно
гомеоморфно ![]() . Пусть
. Пусть
![]() - гомеоморфизм. Отождествляя каждую точку
- гомеоморфизм. Отождествляя каждую точку ![]() с ее образом
с ее образом
![]() , получим новое многообразие
, получим новое многообразие
![]() , называемое склейкой многообразий
, называемое склейкой многообразий ![]() и
и ![]() вдоль гомеоморфизма
вдоль гомеоморфизма ![]() .
.
Построим с помощью этой операции двумерное многообразие, играющее
важную роль в различных областях математики - вещественную
проективную плоскость
![]() .
.
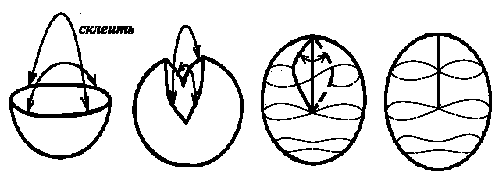
Построение начинается с полусферы, например, заданной условиями
![]() Ее границей является окружность
Ее границей является окружность
![]() получаемая в пересечении сферы плоскостью
получаемая в пересечении сферы плоскостью
![]() (экватор). Рассмотрим гомеоморфизм границы полусферы на
себя, задаваемый центральной симметрией относительно начала
координат
(экватор). Рассмотрим гомеоморфизм границы полусферы на
себя, задаваемый центральной симметрией относительно начала
координат
![]() Вещественная проективная
плоскость получается склеиванием экватора полусферы
вдоль гомеоморфизма
Вещественная проективная
плоскость получается склеиванием экватора полусферы
вдоль гомеоморфизма ![]() (рис. 9). Для получения другой
интерпретации вещественной проективной плоскости рассмотрим
трехмерное аффинное пространство. На множестве всех прямых этого
пространства определено отношение параллельности, которое, как
хорошо известно читателю, является отношением эквивалентности.
Тогда имеется разбиение множества всех прямых трехмерного
пространства на классы параллельности. Каждый такой класс состоит
из (бесконечного!) набора всех прямых пространства,
имеющих данное направление. Класс параллельных прямых может быть
задан направляющим вектором прямой этого класса. Выбор
направляющего вектора не однозначен; все направляющие векторы
данной прямой (и данного класса параллельных прямых) коллинеарны и
имеют ненулевую длину. Тогда каждый класс параллельных прямых
задается направлением, то есть классом ненулевых
коллинеарных векторов.
(рис. 9). Для получения другой
интерпретации вещественной проективной плоскости рассмотрим
трехмерное аффинное пространство. На множестве всех прямых этого
пространства определено отношение параллельности, которое, как
хорошо известно читателю, является отношением эквивалентности.
Тогда имеется разбиение множества всех прямых трехмерного
пространства на классы параллельности. Каждый такой класс состоит
из (бесконечного!) набора всех прямых пространства,
имеющих данное направление. Класс параллельных прямых может быть
задан направляющим вектором прямой этого класса. Выбор
направляющего вектора не однозначен; все направляющие векторы
данной прямой (и данного класса параллельных прямых) коллинеарны и
имеют ненулевую длину. Тогда каждый класс параллельных прямых
задается направлением, то есть классом ненулевых
коллинеарных векторов.
Проективная плоскость - это многообразие, точки которого
соответствуют классам параллельных прямых трехмерного
аффинного пространства или, равносильно, классам
коллинеарности ненулевых векторов трехмерного
векторного пространства. Зафиксируем в нем базис; тогда каждый
вектор
![]() задается координатами
задается координатами
![]() , причем хотя бы одна из координат отлична от
нуля.
, причем хотя бы одна из координат отлична от
нуля.
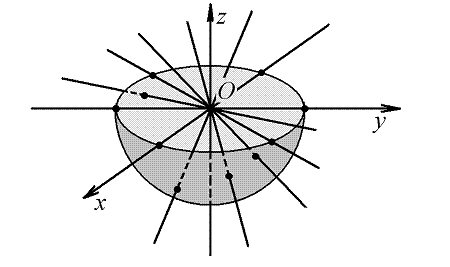
Векторы, принадлежащие
одному направлению, имеют пропорциональные координаты, поэтому
направление может быть задано способом, известным из курса
проективной геометрии как однородные координаты. Однородные
координаты
![]() - это класс пропорциональных
упорядоченных троек чисел, хотя бы одно из которых отлично от
нуля. Каждый из таких классов определяет направление и,
следовательно, точку проективной плоскости. Это соответствие
представлено на рис. 10. Направления изображены в виде прямых,
проходящих через начало координат и пересекающих полусферу, из
которой проективная плоскость получалась путем склейки границы.
Каждая из прямых, не принадлежащих плоскости экваториального
сечения (плоскости
- это класс пропорциональных
упорядоченных троек чисел, хотя бы одно из которых отлично от
нуля. Каждый из таких классов определяет направление и,
следовательно, точку проективной плоскости. Это соответствие
представлено на рис. 10. Направления изображены в виде прямых,
проходящих через начало координат и пересекающих полусферу, из
которой проективная плоскость получалась путем склейки границы.
Каждая из прямых, не принадлежащих плоскости экваториального
сечения (плоскости ![]() ), пересекает полусферу в
единственной точке и таким образом выделяет точку проективной
плоскости, отвечающую данному направлению. Каждая
прямая, принадлежащая плоскости экваториального сечения,
пересекает полусферу в двух точках границы, отождествляемых
склейкой, и, тем самым, также выделяет единственную точку
проективной плоскости.
), пересекает полусферу в
единственной точке и таким образом выделяет точку проективной
плоскости, отвечающую данному направлению. Каждая
прямая, принадлежащая плоскости экваториального сечения,
пересекает полусферу в двух точках границы, отождествляемых
склейкой, и, тем самым, также выделяет единственную точку
проективной плоскости.

Для построения связной суммы многообразий ![]() и
и ![]() одинаковой размерности
одинаковой размерности ![]() выберем окрестности
выберем окрестности ![]() и
и
![]() точек
точек ![]() и
и ![]() соответственно, гомеоморфные
открытому
соответственно, гомеоморфные
открытому ![]() -мерному шару. Очевидно, границы многообразий
-мерному шару. Очевидно, границы многообразий
![]() и
и
![]() гомеоморфны
(
гомеоморфны
(![]() -мерной сфере). Пусть
-мерной сфере). Пусть ![]() - какой-нибудь
гомеоморфизм границ. Тогда связная сумма
- какой-нибудь
гомеоморфизм границ. Тогда связная сумма ![]() многообразий
многообразий
![]() и
и ![]() определяется как их склейка вдоль гомеоморфизма
определяется как их склейка вдоль гомеоморфизма ![]() (рис. 11).
(рис. 11).
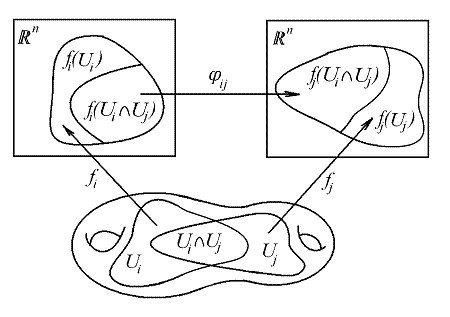
Топологическое многообразие ![]() называется дифференцируемым класса
называется дифференцируемым класса ![]() (или
(или
![]() ), если
гомеоморфные отображения
), если
гомеоморфные отображения
![]() подчинены
следующему условию: для любых
подчинены
следующему условию: для любых ![]() ограничения отображений
ограничения отображений ![]() и
и ![]() согласованы в следующем смысле: определено
отображение
согласованы в следующем смысле: определено
отображение
![]() , задаваемое функциями,
имеющими непрерывные частные производные порядка
, задаваемое функциями,
имеющими непрерывные частные производные порядка ![]() (соответственно, имеющими непрерывные частные производные любого
порядка), такое, что
(соответственно, имеющими непрерывные частные производные любого
порядка), такое, что
![]() (рис. 12). Отображения
(рис. 12). Отображения ![]() называются координатными отображениями, пара
называются координатными отображениями, пара
![]() - картой, а
соответствующий покрытию
- картой, а
соответствующий покрытию
![]() набор
набор
![]() - атласом дифференцируемого многообразия
- атласом дифференцируемого многообразия ![]() . Отображения
. Отображения
![]() иногда называют отображениями склейки.
иногда называют отображениями склейки.
Многообразия класса
![]() называют также аналитическими.
называют также аналитическими.
В качестве примера снабдим двумерный тор структурой
дифференцируемого многообразия. В лекции 3 доказан локальный
гомеоморфизм тора и евклидовой плоскости. Атлас на торе может быть
построен выбором различных начал отсчета угловых координат
![]() и
и ![]() . Рассмотрим построение атласа на торе
подробнее. Назовем параллелью геометрическое место точек
тора, имеющих одно и то же значение угловой координаты
. Рассмотрим построение атласа на торе
подробнее. Назовем параллелью геометрическое место точек
тора, имеющих одно и то же значение угловой координаты ![]() ;
меридианом - геометрическое место точек тора, имеющих одно
и то же значение угловой координаты
;
меридианом - геометрическое место точек тора, имеющих одно
и то же значение угловой координаты ![]() , то есть любую его
образующую.
, то есть любую его
образующую.
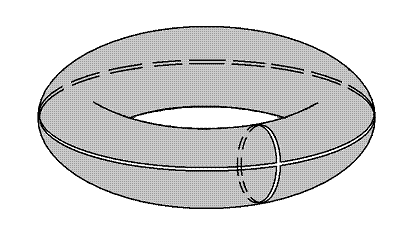
Разрезав тор вдоль выбранных параллели и меридиана (рис. 13),
получим множество точек, гомеоморфное прямоугольнику, называемому
разверткой тора. Введем (новые) координаты на развертке так,
что
![]() соответствует параллели разреза,
соответствует параллели разреза,
![]() и
и
![]() - меридиану разреза. Прямоугольник
- меридиану разреза. Прямоугольник
![]()
![]() c гомеоморфизмом в тор образует
координатную карту.
c гомеоморфизмом в тор образует
координатную карту.
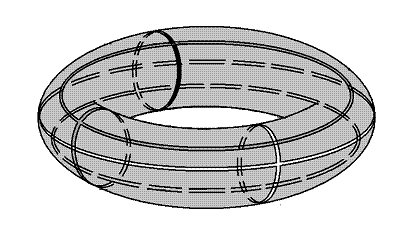
Выберем три пары параллель-меридиан, причем так, что все три
параллели и все три меридиана различны (рис. 14). Каждая такая
пара задает способ отсчета угловых координат на торе только что
описанным образом, причем каждая точка тора покрыта хотя бы одной
из трех карт. Пусть ![]() и
и ![]() - две построенные таким
способом координатные карты, и точка с координатами
- две построенные таким
способом координатные карты, и точка с координатами
![]() в карте
в карте ![]() имеет в карте
имеет в карте ![]() координаты
координаты
![]() . Тогда имеют место
уравнения перехода от координат
. Тогда имеют место
уравнения перехода от координат
![]() в карте
в карте
![]() к координатам
к координатам
![]() в карте
в карте ![]() :
:
Структуры дифференцируемых многообразий нетрудно ввести, например, на сфере, параболоиде вращения и других известных читателю поверхностях второго порядка.
Упражнение. С помощью однородных координат построим
локальные карты на проективной плоскости. Карта ![]() соответствует множеству точек с ненулевой координатой
соответствует множеству точек с ненулевой координатой ![]() ;
координаты в этой карте имеют вид
;
координаты в этой карте имеют вид
![]() .
Аналогично,
.
Аналогично,
![]() Также,
Также,
![]() Выпишите
функции перехода и убедитесь в том, что вещественная проективная
плоскость
Выпишите
функции перехода и убедитесь в том, что вещественная проективная
плоскость
![]() - аналитическое многообразие.
- аналитическое многообразие.