Классическое определение вероятности случайного события предполагает конечное число всех исходов испытания. Но часто встречаются такие испытания, для которых число возможных исходов бесконечно. В этом случае, если позволяют обстоятельства, используют понятие геометрической вероятности.
Геометрической вероятностью события A называется
отношение меры области, благоприятствующей появлению события ![]() ,
к мере всей области исходов
,
к мере всей области исходов ![]()
Пример 56. Две студентки физмата договорились о встрече у деканата на большой перемене (40 мин.), условившись каждая ждать другую не более 10 мин. Какова вероятность того, что встреча состоится?
Решение. Обозначим через ![]() и
и ![]() время в час. прихода к деканату
студенток с начала перемены. Тогда
время в час. прихода к деканату
студенток с начала перемены. Тогда ![]() = {(
= {(![]() / 0
/ 0 ![]()
![]() , 0
, 0
![]() } на
плоскости
} на
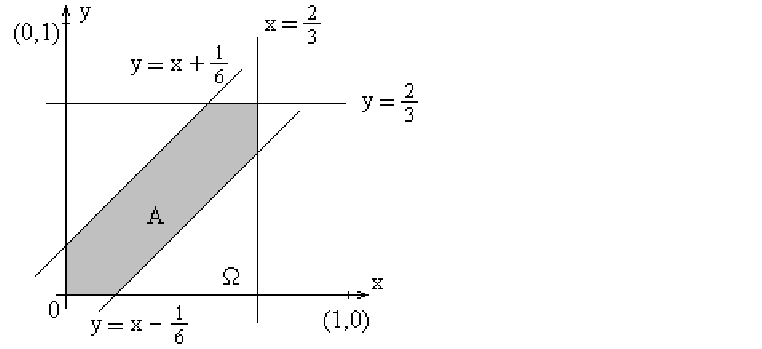
плоскости ![]() (рис. 39).
Область равновозможных значений
(рис. 39).
Область равновозможных значений ![]() и
и ![]() представлена квадратом
представлена квадратом
![]() площадью
площадью
![]() . Область
благоприятных значений
. Область
благоприятных значений
![]() = {встреча состоится} = {(
= {встреча состоится} = {(![]() / 0
/ 0
![]() , 0
, 0
![]() ,
,
![]() }
заключена
между прямыми
}
заключена
между прямыми
![]() и
и
![]() .
.
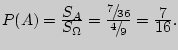
Пример 57. Палка длины ![]() разломана на 3
части.
Найти вероятность
того, что из полученных частей можно составить треугольник.
разломана на 3
части.
Найти вероятность
того, что из полученных частей можно составить треугольник.
Решение. Обозначим через ![]() и
и ![]() длины двух получившихся частей
палки, тогда длина третьей части будет
длины двух получившихся частей
палки, тогда длина третьей части будет ![]()
![]() .
Событие A = {из трех
частей можно составить треугольник} выполняется, когда имеют
место неравенства треугольника:
.
Событие A = {из трех
частей можно составить треугольник} выполняется, когда имеют
место неравенства треугольника:
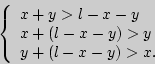
Итак, событие A = {(![]() / 0
/ 0 ![]() , 0
, 0
![]() }
на плоскости
}
на плоскости ![]() представляет треугольник (рис. 40).
представляет треугольник (рис. 40).
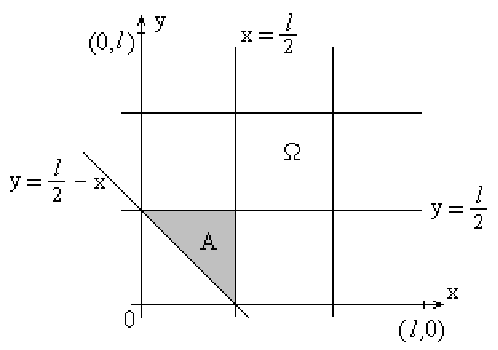
Отсюда
![]()
Рассмотренные выше классическая и геометрическая вероятности побуждают на выделение наиболее существенных и общих для них свойств, которые можно было бы принять в качестве основных аксиом при построении математического основания теории вероятностей.
Пусть каждому событию ![]() ставится в соответствие
некоторое число
ставится в соответствие
некоторое число
![]() , которое удовлетворяет общепринятой системе аксиом
Колмогорова:
, которое удовлетворяет общепринятой системе аксиом
Колмогорова:
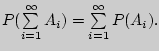
Выведем из предложенных аксиом некоторые "классические" формулы.
Пример 58. Доказать, что
![]()
Решение.
![]() и
и ![]() .
Следовательно, по второй аксиоме
.
Следовательно, по второй аксиоме
![]() и
и ![]()
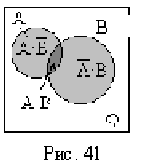
Пример 59. Найти ![]() .
.
Решение.
![]() .
По следствию из второй аксиомы
.
По следствию из второй аксиомы
![]() Но
Но
![]() ;
;
![]()
![]()
![]() откуда
откуда
![]() и
и
![]() Следовательно,
Следовательно,
![]()
Пример 60. Доказать, что
![]() где
где
![]()
Решение.
![]() и
и
![]() .
Используем результат примера 58:
.
Используем результат примера 58:
Тогда ![]() (A
(A![]() B)=
B)=
![]()
Вопросы для самоконтроля
Задачи