В §9 мы уже рассматривали некоторые известные игры (различные "считалки", например) и оценивали вероятности игроков на победу в них. В этом разделе будем рассматривать такие азартные игры, которые допускают их оценки через характеристики положения (математическое ожидание, медиану и моду) случайной величины выигрыша (числа набранных очков). Игра называется безобидной, если математическое ожидание величины выигрыша равно нулю, а по его знаку ("плюс" или "минус") судим о приемлемости принятия этих условий для участия в игре.
Пример 76. Азартному человеку предлагаются следующие условия игры: если он достанет из полного набора домино кость с суммой очков 3, 6 или 9, то он получит приз в размере 9, 6 или 3 долларов соответственно, в противном случае он платит организаторам 2 доллара. Принимать ли ему участие в игре по таким правилам?
Решение. ![]() = {величина выигрыша участника} = {-2, 3,
6, 9}. Обратим внимание, что 3 очка в сумме можно получить
двумя способами (0+3 = 1+2), 6 очков - четырьмя (0+6 = 1+5 = 2+4
= 3+3), 9 очков - тоже двумя (3+6 = 4+5), а остальные 20 случаев
дают другие суммы. По графу распределения с.в.
= {величина выигрыша участника} = {-2, 3,
6, 9}. Обратим внимание, что 3 очка в сумме можно получить
двумя способами (0+3 = 1+2), 6 очков - четырьмя (0+6 = 1+5 = 2+4
= 3+3), 9 очков - тоже двумя (3+6 = 4+5), а остальные 20 случаев
дают другие суммы. По графу распределения с.в. ![]() находим
находим
![]() [
[![]() ].
].
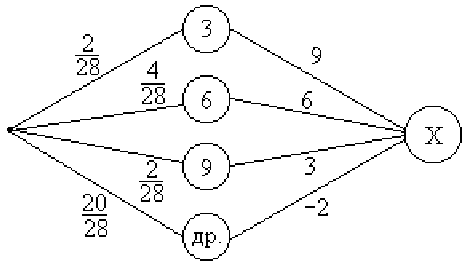
Из решения видно, что игра будет безобидной, если установить плату
за участие в игре в размере ![]() долларов.
долларов.
Пример 77. Два игрока бросают игральную кость сериями по очереди, складывая количество выпавших очков, в любой момент игрок может остановиться и передать ход другому игроку, но, если выпало 1 очко, то очки серии "сгорают" и ход автоматически передается противнику. Какой стратегии выгодней придерживаться игроку?
Решение. Возможны два подхода к выбору стратегии:
1) по количеству набранных очков в серии;
2) по числу подбрасываний в серии.
Стратегия №1 (по количеству набранных очков).
Пусть мы набрали ![]() очков в данной серии.
очков в данной серии.
Случайная величина ![]() = {число очков серии после следующего броска}.
= {число очков серии после следующего броска}.
Построим граф распределения с.в. ![]() :
:
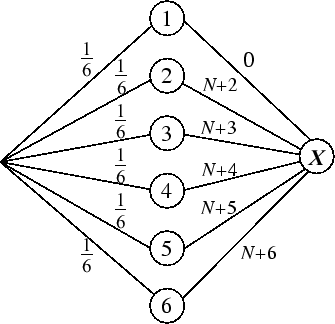
Найдем математическое ожидание как вес всего графа.
![]() Продолжение станет невыгодным,
если
Продолжение станет невыгодным,
если ![]() [
[![]() ]
] ![]() N:
N:
![]() (5N +
20)
(5N +
20) ![]() N,
N, ![]()
![]() 20, при
20, при
![]()
![]() 20 продолжение игры становится для
игрока невыгодным. Следовательно, можно предложить игроку бросать
игральную кость в серии до появления в сумме от 19 до 24 очков и
передать ход другому игроку.
20 продолжение игры становится для
игрока невыгодным. Следовательно, можно предложить игроку бросать
игральную кость в серии до появления в сумме от 19 до 24 очков и
передать ход другому игроку.
Стратегия №2 (по числу сделанных бросков).
Пусть ![]() число бросков.
число бросков.
Случайная величина ![]() = {число очков при одном бросании}.
= {число очков при одном бросании}.
Случайная величина ![]() имеет следующий закон распределения
имеет следующий закон распределения
| 0 | 2 | 3 | 4 | 5 | 6 | |
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Найдем математическое ожидание с.в. ![]()
![]() тогда
тогда
![]()
Заметим, что ![]() [n
[n![]() X
X![]() ] является случайной величиной. Вычислим математическое
ожидание с.в.
] является случайной величиной. Вычислим математическое
ожидание с.в. ![]() [n
[n![]() X
X![]() ]. Составим закон распределения для с.в.
]. Составим закон распределения для с.в. ![]() [n
[n![]() X
X![]() ].
].
|
|
0 | |
| P |
|
|
Продолжение серии бросков будет невыгодным, если
![]() т.е.
т.е.
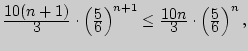
(![]() +1)
+1)
![]()
![]()
Значит, следует делать не более 5-ти бросков в серии.
Пример 78. Два игрока бросают две монеты сериями по очереди, складывая количество выпавших "гербов", за каждый выпавший "герб" игрок получает одно очко, в любой момент игрок может остановиться и передать ход другому игроку, но если не выпало ни одного "герба", то очки серии "сгорают" и ход передается другому игроку. Какой стратегии выгодней придерживаться игроку?
Решение 1 (по числу набранных очков)
Пусть мы набрали ![]() очков в данной серии, а случайная величина
очков в данной серии, а случайная величина ![]() = {число
очков серии после следующего броска}.
= {число
очков серии после следующего броска}.
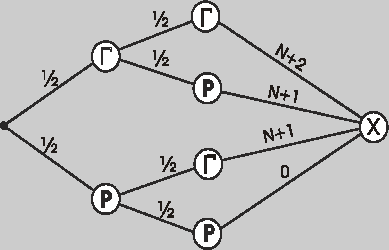
Построим граф распределения и найдем математическое ожидание с.в.
![]() .
.
![]()
Продолжение станет невыгодным, если ![]() , т.е.
, т.е.
![]()
![]()
При ![]()
![]() 4 продолжение игры становится для игрока невыгодным.
4 продолжение игры становится для игрока невыгодным.
Следовательно, можно предложить игроку бросать пару монет в серии до появления в сумме 3 или 4 очков и передать ход другому игроку.
Решение 2 (по числу сделанных бросков)
Пусть ![]() число бросков. Случайная величина
число бросков. Случайная величина ![]() = {число очков при одном
бросании}. Случайная величина
= {число очков при одном
бросании}. Случайная величина ![]() имеет следующий закон распределения.
имеет следующий закон распределения.
Найдем математическое ожидание с.в. ![]()
![]() [
[![]() ] = 0
] = 0
![]() + 1
+ 1
![]() + 2
+ 2
![]() = 1.
= 1.
![]() [
[![]() ] =
] = ![]() [
[![]() ] =
] = ![]() . Заметим, что
. Заметим, что ![]() [
[![]() ]
является случайной величиной. Вычислим математическое ожидание с.в.
]
является случайной величиной. Вычислим математическое ожидание с.в.
![]() [
[![]() ]. Составим закон распределения для
]. Составим закон распределения для ![]() [
[![]() ],
учитывая, что очки "не сгорят" (если ни разу не выпадет пара "решек")
],
учитывая, что очки "не сгорят" (если ни разу не выпадет пара "решек")
![]() [
[![]() [
[![]() ]] =
]] =
![]() ;
;
![]() [
[![]() [(
[(![]() +1)
+1)![]() ]] = (
]] = (![]() +1)
+1)![]() (
(
![]() .
Продолжение серии бросков будет невыгодным, если
.
Продолжение серии бросков будет невыгодным, если
![]() [
[![]() [(
[(![]() +1)
+1)![]() ]]
]] ![]() [
[![]() [
[![]() ]], т.е.
]], т.е.
(![]() +1)
+1)![]() (
(
![]() ;
;
(![]() +1)
+1)
![]() ;
;
![]() 3.
3.
Значит, следует делать не более 3-х бросков.
Сравним эффективность предложенных двух подходов в определении стратегии: по количеству набранных очков и по количеству подбрасываний в серии. Для этого найдем математические ожидания набранных очков в серии.
1) Прекратим испытания при появлении 3-х очков в серии.
![$\begin{array}{l}
M[X] = (1 + 1 + 1) \cdot {\displaystyle 1\over\displaystyle 2...
...playstyle 8} = {\displaystyle 13\over\displaystyle 8} = 1,625. \\
\end{array}$](img794.png)
2) Прекратим испытания при появлении по крайней мере 4-х очков в серии.
Построим вероятностное дерево исходов:
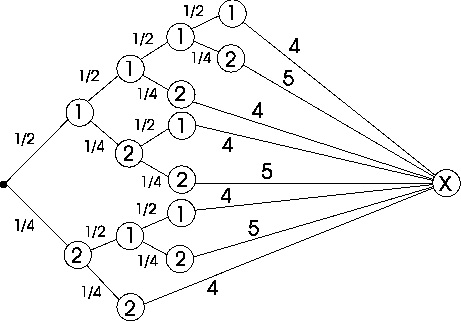
По числу бросков ![]() = 3,
= 3, ![]() [
[![]() ] = 3
] = 3
![]() 1,26
1,26
1,72 > 1,625 > 1,26, следовательно, более эффективна первая стратегия (по числу набранных очков в серии).
Пример 79. Два игрока ставят свои монеты одного достоинства на одну из клеток полосы с натуральными номерами. Фишку устанавливают на клетку с номером первого появления шестерки при повторных подбрасываниях игральной кости. На какую клетку лучше поставить свою монету, если победитель определяется по наименьшему расстоянию от фишки до монеты участника?
Решение. Свою монету разумно поставить на медиану M![]() случайной величины
случайной величины ![]() = {номер выпадения шести очков при
подбрасывании кости}. В нашем случае M
= {номер выпадения шести очков при
подбрасывании кости}. В нашем случае M![]() = 4, т.к.
= 4, т.к.
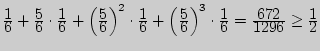 и
и
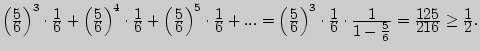
Пример 80. Два игрока ставят свои монеты на клетки полосы с целыми неотрицательными номерами. Фишку устанавливают на клетку с номером, соответствующим числу выпадения "герба" при шести подбрасываниях монеты. На какую клетку выгодно поставить свою монету, если победитель определяется по близости фишки до монеты участника?
Решение. Как и в решении предыдущей задачи, можно посоветовать
поставить монету на медиану M![]() с.в.
с.в. ![]() = {число
выпадений "герба" при шести подбрасываниях монеты}. M
= {число
выпадений "герба" при шести подбрасываниях монеты}. M![]() = 4, поскольку
= 4, поскольку
![]() и
и
![]()
Последние два примера на использование медианы геометрического и биномиального законов распределения.
Вопросы для самоконтроля
1. Приведите пример азартной игры.
2. Какие типы азартных игр вы знаете?
3. Что понимают под безобидностью игры?
4. В чем заключается парадокс "Санкт-Петербургского парадокса"?
5. Какие характеристики случайных величин чаще используются при поиске стратегии игр?
6. Приведите примеры игр со "сгорающими" очками.
7. Какие подходы возможны к стратегиям игр со "сгорающими" очками?
8. Ваш совет в установлении ставок в азартной игре.
Задачи
I 151. Из колоды в 32 карты достают по одной с возвратом две карты. Стои-мость участия в игре составляет один доллар, а приз в размере одного доллара выплачивается за каждую козырную карту. Принимать ли участие в этой игре?
152. Азартному студенту предлагаются следующие условия игры: если он достает из полного набора домино кость с суммой очков 3, 6 или 9, то по-лучит равную им сумму долларов, в противном случае он платит органи-заторам 2 доллара. Принимать ли ему участие в игре по таким правилам?
153. В условиях предыдущей задачи определить, какую следует установить плату за участие, чтобы игра была безобидной.
154. Из колоды в 36 карт извлекли две карты (без возврата) и выплачиваем приз в размере 10 рублей за каждую козырную карту. Каким должен быть вступительный взнос, чтобы игра была безобидной?
155. Бросаем игральный кубик до появления шести очков и устанавливаем приз в рублях, равный номеру выпадения шестерки. Каким должен быть вступительный взнос, чтобы игра была безобидной?
156. Организатор предлагает выплатить за каждый выпавший "герб" при пяти подбрасываниях монеты 16 рублей. Какой должна быть величина стоимости участия в игре, чтобы она была выгодной для организатора?
II 157. Два игрока ставят свои монеты одного достоинства на одну из клеток полосы с натуральными номерами. Фишку устанавливают на клетку с номером первого появления шестерки при повторных подбрасываниях игральной кости. На какую клетку лучше поставить свою монету, если победитель определяется по наименьшему расстоянию от фишки до монеты участника?
158. В условиях предыдущей задачи заменим подбрасывание игральной кости на подбрасывание двух монет до появления "гербов" на обеих монетах.
III 159. Два игрока подбрасывают игральную кость сериями, суммируя выпавшие очки от 1 до 5, а при выпадении шестерки очки данной серии "сго-рают" и ход передается другому участнику. Победитель определяется по наи-большей сумме очков всех серий. Какой стратегии придерживаться игроку?
160. В условиях предыдущей задачи заменим подбрасывание игральной кости на подбрасывание трех монет и суммирование числа "гербов", при отсутствии "гербов" очки серии сгорают.