(
Если на пространстве событий ![]() =
{
=
{![]() } заданы две случайные функции
} заданы две случайные функции ![]() =
=
![]() (
(![]() ) и
) и ![]() =
= ![]() (
(![]() ), то говорят, что задана двумерная случайная
величина
), то говорят, что задана двумерная случайная
величина
(![]() ,
, ![]() ).
).
Интегральной функцией распределения двумерной случайной величины
(![]() ,
, ![]() ) называется вероятность совместного выполнения двух
неравенств:
) называется вероятность совместного выполнения двух
неравенств: ![]() и
и ![]() :
:
и геометрически определяет вероятность попадания
случайной точки (![]() ,
,![]() ) в бесконечный квадрат с вершиной в точке
(
) в бесконечный квадрат с вершиной в точке
(![]() ,
, ![]() ), лежащей левее и ниже ее.
), лежащей левее и ниже ее.
Закон распределения дискретной двумерной с.в. (![]() ,
,![]() ) может быть
задан с помощью таблицы
) может быть
задан с помощью таблицы
Для двумерной с.в. (![]() ,
, ![]() ) дискретного и непрерывного типов интегральные
функции распределения соответственно равны
) дискретного и непрерывного типов интегральные
функции распределения соответственно равны
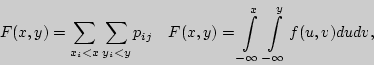
где ![]() ,
, ![]() - плотность вероятности величины (
- плотность вероятности величины (![]() ,
, ![]() ).
).
Свойства функции плотности вероятности:
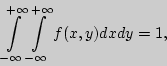
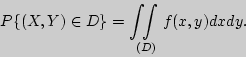
Пример 96. Составить закон распределения двух шаров в первых двух ящиках, если два шара случайно размещаются по трем ящикам.
Решение. Пусть ![]() = {число шаров в первом ящике} и
= {число шаров в первом ящике} и ![]() = {число шаров во
втором ящике}, тогда искомый закон совместного распределения с.в. (
= {число шаров во
втором ящике}, тогда искомый закон совместного распределения с.в. (![]() ,
, ![]() )
представляется следующей таблицей:
)
представляется следующей таблицей:
| 0 | 1 | 2 | Распределение |
|
| 0 |
|
|
|
|
| 1 |
|
|
0 |
|
| 2 |
|
0 | 0 |
|
| Распределение |
|
|
|
Пример 97. Найти интегральную функцию распределения для числа
попаданий и числа промахов по мишени при одном выстреле, вероятность
попадания при котором равна ![]() .
.
Решение. Пусть ![]() = {число попаданий в мишень} и
= {число попаданий в мишень} и ![]() = {число промахов
по мишени}, тогда закон распределения двумерной с.в. (
= {число промахов
по мишени}, тогда закон распределения двумерной с.в. (![]() ,
, ![]() ) будет
следующий:
) будет
следующий:
а искомая интегральная функция
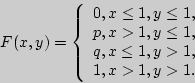
Пример 98. Составить закон распределения для суммы очков на "костях" из полного набора домино и для их абсолютных разностей, взятых по модулю 3.
Решение. Для каждой из "кости" домино найдем соответствующую им пару чисел
![]() = {сумма очков на "кости" по mod 3} и
= {сумма очков на "кости" по mod 3} и ![]() = {абсолютная разность
очков на "кости" по mod 3}. Так, "костям"
= {абсолютная разность
очков на "кости" по mod 3}. Так, "костям"
соответствует одна пара чисел (![]() ,
, ![]() а именно (0, 0).
а именно (0, 0).
Таким образом можно получить следующий закон распределения двумерной с.в.
(![]() ,
,![]() ):
):
Пример 99. Двумерная с.в. (![]() ,
, ![]() ) имеет плотность вероятности
) имеет плотность вероятности
Найти а) величину ![]() ; б) функцию распределения
; б) функцию распределения ![]() ,
, ![]() ; в)
вероятность попадания случайной точки (
; в)
вероятность попадания случайной точки (![]() ,
, ![]() в прямоугольник,
ограниченный прямыми
в прямоугольник,
ограниченный прямыми ![]() = 0,
= 0, ![]() = 0,
= 0, ![]() = 1,
= 1, ![]()
Решение. а). Поскольку
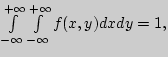 то
то
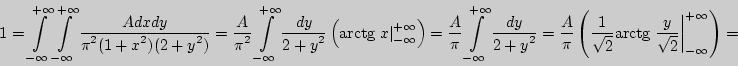
б).
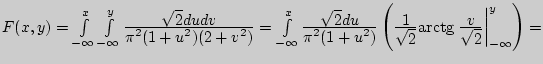
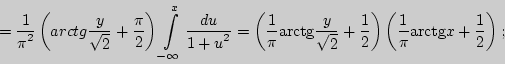
в).
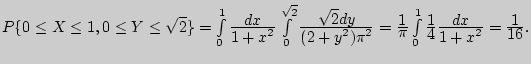
Пример 100. Найти ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() /
/![]() ,
, ![]() /
/![]() для функции плотности вероятности
для функции плотности вероятности
Решение.
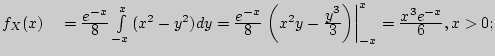
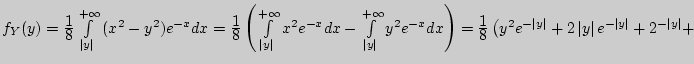
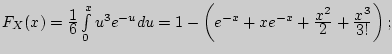
![]() > 0;
> 0;
![]() = 1 -
= 1 - ![]() (-
(-![]() ,
, ![]() < 0.
< 0.
Вопросы для самоконтроля
1. Какие способы задания двумерной случайной величины вы знаете?
2. Геометрический смысл интегральной функции распределения.
3. Как найти центр рассеивания двумерной случайной величины?
4. Свойства интегральной функции распределения.
5. Вычисление условных математических ожиданий на графе распределения.
6. Что называется линией регрессии?
7. Как находятся условные плотности распределения?
8. Как определить независимость составляющих двумерной случайной величины?
Задачи
I 191. Найти закон распределения для числа белых и черных шаров при извлечении двух шаров из урны, содержащей один белый и два черных шара.
192. Составить закон распределения для сумм очков на "костях" из полного набора домино, взятых по модулю 4, и для их разностей по модулю 2.
193. Составить закон распределения для сумм очков на "костях" из полного набора домино, взятых по модулю 4, и для их абсолютных разностей.
194. Найти интегральную функцию распределения для числа "гербов" и "решек" при одном подбрасывании монеты.
195. Двумерная случайная величина задана дифференциальной функцией
Найти постоянную ![]() .
.
196. Найти условные математического ожидания двумерной случайной величины, заданной законом распределения:
II 197. Найти линию регрессии ![]() на
на ![]() для двумерной случайной
величины из предыдущего примера.
для двумерной случайной
величины из предыдущего примера.
198. Двумерная случайная величина (![]() ,
, ![]() ) имеет плотность
вероятности
) имеет плотность
вероятности
Найти: а) величину ![]() ; б) функцию распределения
; б) функцию распределения ![]() ,
, ![]() ; в)
вероятность попадания случайной точки
; в)
вероятность попадания случайной точки ![]() в прямоугольник,
ограниченный прямыми
в прямоугольник,
ограниченный прямыми ![]() = 0,
= 0, ![]() = 0,
= 0, ![]() = 1,
= 1, ![]() .
.
III 199. Плотность распределения непрерывной двумерной
случайной величины ![]() = cos
= cos ![]() cos
cos ![]() в
квадрате
в
квадрате
![]() ,
,
![]() ; вне квадрата
; вне квадрата ![]() = 0. Доказать, что составляющие
= 0. Доказать, что составляющие ![]() и
и ![]() независимы.
независимы.
200. Найти линию регрессии для двумерной дискретной случайной величины из примера 182 [перейти].