Далее: §22. Корреляционный граф многомерных Вверх: Глава III. Случайные величины Назад: §20. Двумерные случайные величины

§21. Характеристики двумерных случайных величин

В качестве числовых характеристик двумерных случайных величин ($X$,$Y$) обычно рассматриваются начальные и центральные моменты различных порядков.

Математическое ожидание произведения

($X$ - $a)^{k}\cdot (Y$ - $b)^{s}$

называется моментом порядка $k+s$. Если $a=b$ = 0, то моменты называются начальными и обозначаются $\alpha$$_{k,s}$; если $a=M$[$X$] и $b=M$[$Y$], то моменты называются центральными - $\mu$$_{k,s}$.

Начальный и центральный моменты дискретных и непрерывных с.в. ($X$,$Y$) определяются по следующим формулам:

$\alpha$ $_{k,s} \quad = \sum\limits_i {\sum\limits_j {x_i ^k \cdot y_j ^s \cdot p_{ij} } } ,$ $\alpha$ $_{k,s} = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {x^ky^sf(x,y)dxdy} } ,$

$\mu$ $_{k,s} = \sum\limits_i {\sum\limits_j {(x_i - \bar {x})^k \cdot (y_j - \bar {y})^s \cdot p_{ij} } } ,$ $\mu$ $_{k,s} = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {(x - \bar {x})^k(y - \bar {y})^sf(x,y)dxdy} } .$

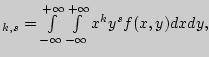
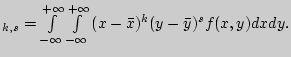
Порядком начального (центрального) момента называется сумма его индексов $k$ + $s.$На практике чаще всего встречаются моменты первого и второго порядков.

Начальные моменты первого порядка представляют собой математические ожидания с.в. $X$ и $Y$. Точка ($M$[$X$],$M$[$Y$]) называется центром рассеивания двумерной с.в. ($X$,$Y$).

Центральные моменты первого порядка равны нулю, а второго:

$\mu$ $_{2,0}=M\left[ {\mathop X\limits^o}^2 \cdot {\mathop Y\limits^o}^0 \right] = M\left[ {\mathop X\limits^o}^2 \right] = D\left[ X \right]{\rm };$

$\mu$ $_{0,2}=M\left[ {\mathop X\limits^o}^0 \cdot {\mathop Y\limits^o}^2 \right] = M\left[ {\mathop Y\limits^o}^2 \right] = D\left[ Y \right]{\rm };$

$\mu$ $_{1,1}=M\left[ {\mathop X\limits^o \cdot \mathop Y\limits^o } \right].$

$\mu$$_{1,1}$ называется ковариацией (или корреляционным моментом) с.в. ($X,Y)$, будем его обозначать

$$Cov(X,Y) = M\left[ {\mathop X\limits^o \cdot \mathop Y\limits^o } \right] = M\left[ {(X - \bar {x})(Y - \bar {y})} \right].$$

Ковариация двух с.в. ($X,Y)$ характеризует не только степень зависимости случайных величин (ковариация двух независимых с.в. равна нулю), но также их рассеивание вокруг точки $(\bar {x},\bar {y})$.

Для характеристики линейной зависимости между $X$ и $Y$ служит коэффициент корреляции

$$\rho (X,Y) = {\displaystyle Cov(X,Y)\over\displaystyle \sqrt {D[X]D[Y]} }.$$

Абсолютное значение коэффициента корреляции максимально (т.е. равно 1), когда между $X$ и $Y$ существует линейная зависимость. Случайные величины $X$ и $Y$ называются некоррелированными, если $\rho$($X,Y)$ = 0.

Коэффициент корреляции является одним из основных понятий в теории вероятностей и математической статистике, был введен Ф. Гальтоном и Пирсоном.

Для конечных с.в.$X, Y$ ковариацию (и аналогично начальные и центральные моменты) удобно находить как полный вес графа, который будем называть ковариационным:

Рис. 57

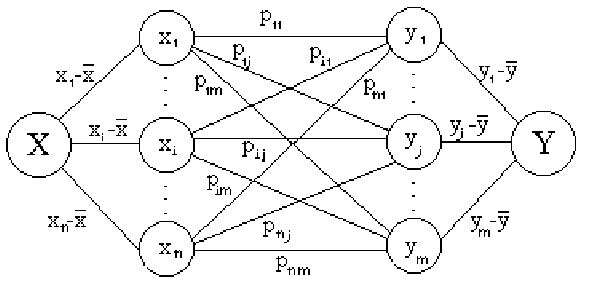
Условным математическим ожиданием одной из с.в. называется ее математическое ожидание, вычисленное при условии, что другая с.в. приняла определенное значение:

$$M[Y / x_i ] = \sum\limits_j {y_i \cdot P\{Y = y_j / X = x_i \}.}$$

Для непрерывных с.в. $X$ и $Y$

$M[Y / x_i ] = \int\limits_{ - \infty }^{ + \infty } {y \cdot f(y / x)dy,} {\rm г}{\rm д}{\rm е}f (y$/$x)$ - условная плотность распределения с.в. $Y$при $X$ = $x$.

Условное математическое ожидание с.в. при заданном $X=x$ называется регрессией $Y$ на $X$. График этой зависимости от $x$ называется линией регрессии $Y$ на $x$. Пример 102. Найти ковариацию для двумерной случайной величины из примера 96 [перейти].

Решение. Во-первых, вычислим математические ожидания с.в. $X$ и $Y$:

$$\bar {х} = 0 \cdot {\displaystyle 4\over\displaystyle 9} + 1... ...aystyle 9} = {\displaystyle 2\over\displaystyle 3} = \bar {у}.$$

Во-вторых, построим ковариационный граф:

Рис. 58

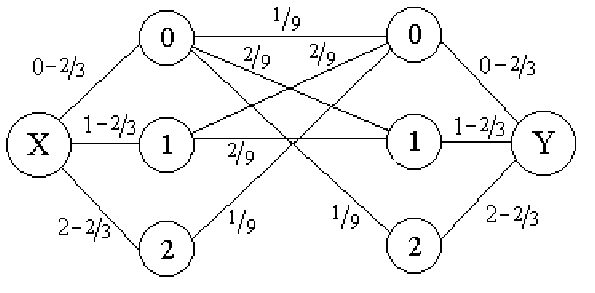
В-третьих, ковариацию находим как вес полученного ковариационного графа:

$$Cov(X,Y) = \left( { - {\displaystyle 2\over\displaystyle 3}}... ...er\displaystyle 81} = - {\displaystyle 2\over\displaystyle 9}.$$

Пример 103. Из урны, содержащей один белый, два черных и три красных шара, последовательно извлекаем два шара. Найти коэффициент корреляции для числа белых ($X)$ и черных ($Y$) шаров, оказавшихся в выборке.

Решение. Построим сначала, как мы это делали в предыдущей главе, вероятностное дерево исходов, добавив к нему два столбца для значений случайных величин $X$ и $Y$.

Рис. 59

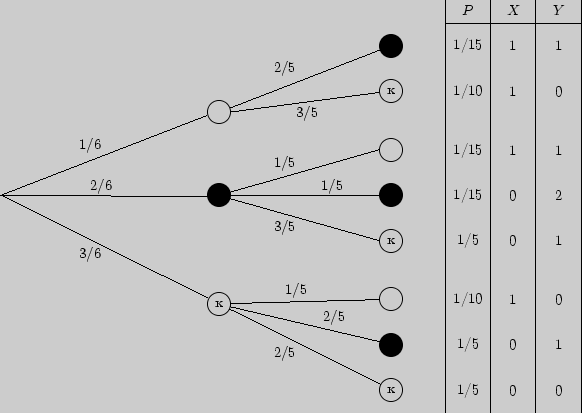
По полученным данным построим ковариационный граф:

$$\bar {х} = 1 \cdot \left( {{\displaystyle 1\over\displaystyle... ...1\over\displaystyle 15} = {\displaystyle 2\over\displaystyle 3}$$

$$Cov(X,Y) = \left( { - {\displaystyle 1\over\displaystyle 3}}... ...er\displaystyle 3} = - {\displaystyle 4\over\displaystyle 45}.$$

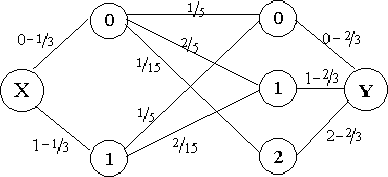
Для получения коэффициента корреляции найдем дисперсии с.в. $X$ и $Y$ по ковариационному графу:

$$D[X] = \left( { - {\displaystyle 1\over\displaystyle 3}} \ri... ...laystyle 15}} \right) = {\displaystyle 2\over\displaystyle 9},$$

$$D[Y] = \left( { - {\displaystyle 2\over\displaystyle 3}} \ri... ...er\displaystyle 15} = {\displaystyle 16\over\displaystyle 45}.$$

Тогда $\rho (X,Y) = {\displaystyle Cov(X,Y)\over\displaystyle \sqrt {D[X] \cdot D[Y]} ... ...ystyle 45 \cdot 4\sqrt 2 } = - {\displaystyle 1\over\displaystyle \sqrt {10} }.$

Пример 104. Показать, что для любых случайных величин $X$ и $Y$ с конечной дисперсией $D$[$X$] выполняется соотношение

$$D[X] = M[D(X / Y)] + D[M(X / Y)].$$

Решение. По свойству дисперсии

$$M\left[ {D(X / Y)} \right] = M\left[ {M(X^2 / Y) - M^2(X / Y... ... M\left[ {M(X^2 / Y)} \right] - M\left[ {M^2(X / Y)} \right] =$$

$$= M\left[ {X^2} \right] - M^2\left[ X \right] = D\left[ X \... ...]{\rm и }M\left[ {M(X^2 / Y)} \right] = M\left[ {X^2} \right].$$

Пример 105. Найти коэффициент корреляции двумерной случайной величины из примера 99[перейти].

Решение. Найдем математические ожидания с.в. $X$ и $Y$:

$$M[X] = \alpha _{1,0} = \int\limits_{ - \infty }^{ + \infty }... ...^2}} } \right)} {\displaystyle dy\over\displaystyle 2 + y^2} =$$

$$\begin{array}{l} = {\displaystyle \sqrt 2 \over\displaystyl... ...isplaystyle dy\over\displaystyle 2 + y^2} = 0. \\ \end{array}$$

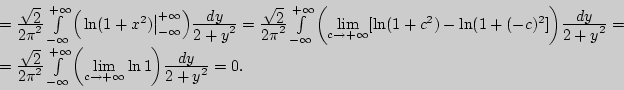
Аналогично получаем, что $M$[$Y$] = 0.

Тогда $Cov(X,Y) = M[(X - 0) \cdot (Y - 0)] = \int\limits_{ - \infty }^{ + \infty } {\i... ...style 1 + x^2}dx} } \right){\displaystyle ydy\over\displaystyle 2 + y^2}} = 0.$

Следовательно, $\rho (X,Y) = {\displaystyle Cov(X,Y)\over\displaystyle \sqrt {D[X] \cdot D[Y]} } = 0$.

Вопросы для самоконтроля

1. Порядок начального (центрального) момента.

2. Что характеризует ковариация?

3. Чему равна ковариация двух независимых случайных величин?

4. Ковариационный граф.

5. Кто ввел понятие коэффициента корреляции?

6. Каково максимальное абсолютное значение коэффициента корреляции? Приведите примеры.

7. Какие случайные величины называются некоррелированными?

8. Нахождение коэффициента корреляции по ковариационому графу.

Задачи

I 201. Найти начальные моменты первого и второго порядков для двумерной случайной величины, заданной законом распределения:

X / Y	-1	0	1	2
-1	0,1	0,2	0,05	0,15
1	0,05	0,1	0,25	0,1

202. Построить ковариационный граф для двумерной дискретной случайной величины из примера 183.

203. Заданы плотности распределения независимых составляющих непрерывной двумерной случайной величины ($X$, $Y$):

$$f_1 (x) = \left\{ {\begin{array}{l} 0,{\rm при }х < 0, \\ ... ..., \\ 2e^{ - 2x},{\rm при }х \ge 0, \\ \end{array}} \right.$$

Найти: а) плотность совместного распределения системы; б) ковариацию двумерной случайной величины ($X, Y$).

204. Доказать, что для любых постоянных $a, b, c, d$ справедливо равенство $Cov (aX+ b, cY + d) = ac Cov (X, Y)$.

205. Найти ковариацию для сумм очков и числа тузов при выборе двух карт из колоды, содержащей только тузов, королей и дам.

206. Найти ковариацию для числа простых цифр в двузначном числе и числа простых двузначных чисел.

II 207. Найти коэффициент корреляции для числа нечетных цифр и числа простых двузначных чисел, получающихся при последовательном извлечении двух простых цифр, написанных на карточках.

208. Задана плотность совместного распределения непрерывной двумерной случайной величины $(X,Y)$: $f(x, y)=\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$} \sin x \cdot \sin y$ в квадрате $0 \le х \le \pi ,0 \le у \le \pi$; вне квадрата $f (х, у) = 0$. Найти коэффициент корреляции $\rho (x, y)$.

III 209. Приведите пример, показывающий, что из равенства нулю коэффициента корреляции не следует независимость соответствующих случайных величин.

210. Докажите, что если $X$ и $Y$ связаны линейной зависимостью $Y$ = aX + $b$, то абсолютная величина коэффициента корреляции равна единице.

Далее: §22. Корреляционный граф многомерных Вверх: Глава III. Случайные величины Назад: §20. Двумерные случайные величины