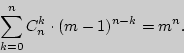Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.
Правило суммы. Если некоторый объект ![]() можно выбрать
можно выбрать
![]() способами, а другой объект
способами, а другой объект ![]() можно выбрать
можно выбрать ![]() способами, то
выбор "либо
способами, то
выбор "либо ![]() , либо
, либо ![]() " можно
осуществить
" можно
осуществить ![]() способами.
способами.
Правило произведения. Если объект ![]() можно выбрать
можно выбрать ![]() способами, а после каждого такого выбора другой объект
способами, а после каждого такого выбора другой объект ![]() можно
выбрать (независимо от выбора объекта
можно
выбрать (независимо от выбора объекта ![]() способами, то
пары объектов
способами, то
пары объектов ![]() и
и ![]() можно выбрать
можно выбрать ![]() способами.
способами.
Пусть ![]() = {
= {![]() ,
, ![]() ,
...,
,
..., ![]() },
}, ![]() =
{
=
{![]() ,
, ![]() , ...,
, ..., ![]() } и
} и ![]() А
А ![]() - число элементов множества
- число элементов множества ![]() . Составим декартово
произведение
. Составим декартово
произведение
![]() множеств
множеств ![]() и
и ![]() ,
т.е. множество пар (
,
т.е. множество пар (![]() ,
,
![]() .
.
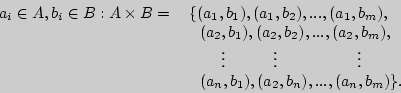
Тогда правило произведения записывается следующим образом:
Пример 6. Сколько существует двузначных чисел?
Решение. Поскольку в двузначном числе цифра, обозначающая число
десятков, должна быть отлична от нуля, то ![]() =
{1, 2, ...,
9},
=
{1, 2, ...,
9}, ![]() = {0, 1, 2, ..., 9} и
= {0, 1, 2, ..., 9} и
![]()
Размещениями из ![]() элементов по
элементов по ![]() называются такие выборки, которые,
имея по
называются такие выборки, которые,
имея по ![]() элементов, выбранных из числа данных
элементов, выбранных из числа данных ![]() элементов, отличаются одна от
другой либо составом элементов, либо порядком их расположения.
элементов, отличаются одна от
другой либо составом элементов, либо порядком их расположения.
Число размещений из ![]() элементов по
элементов по ![]() обозначим
обозначим ![]() Используя основное правило комбинаторики, получаем
Используя основное правило комбинаторики, получаем
Если ![]() , то
, то ![]() - число
таких
размещений, которые
отличаются только порядком расположения элементов. Такие
размещения называются перестановками. Их число
- число
таких
размещений, которые
отличаются только порядком расположения элементов. Такие
размещения называются перестановками. Их число ![]() находится по формуле
находится по формуле
Выборки из ![]() элементов, взятых из данных
элементов, взятых из данных ![]() ,
отличающихся
только составом элементов, называются сочетаниями из
,
отличающихся
только составом элементов, называются сочетаниями из ![]() элементов по
элементов по ![]() . Число
. Число ![]() таких
сочетаний
находится
таких
сочетаний
находится
Пример 7. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, немецкого, французского, испанского - на любой другой из этих пяти языков?
Решение. Поскольку важен порядок, с какого языка задается перевод на другой, то для ответа на вопрос необходимо найти число размещений из пяти по два.
Пример 8. В соревнованиях на первенство университета по волейболу участвуют 8 команд. Насколько более продолжительным будет турнир, организованный по круговой системе, чем по олимпийской?
Решение. При проведении турнира по круговой системе каждый
участник встречался с каждым и порядок их вхождения в пару не
важен. Следовательно, по круговой системе потребуется провести
![]() встреч,
а по олимпийской только - 7 (четыре встречи в
встреч,
а по олимпийской только - 7 (четыре встречи в
![]() финала,
две - в
полуфинале и одна в финале).
финала,
две - в
полуфинале и одна в финале).
В данных выборках допускается повторение элементов, что является достаточно естественным (например, в телефонных и автомобильных номерах возможно использование одной цифры несколько раз).
Число размещений из ![]() элементов по
элементов по ![]() с повторениями
обозначается
с повторениями
обозначается ![]() и находится как
и находится как
Число перестановок ![]() , в которых
1-й элемент повторяется
, в которых
1-й элемент повторяется ![]() раз, 2-й -
раз, 2-й - ![]() раз,
а
раз,
а ![]() -й -
-й -
![]() раз, находится следующим образом:
раз, находится следующим образом:
Пример 9. Сколько "слов" можно получить, переставляя буквы в слове МАТЕМАТИКА?
Решение. Заметим, что если бы все буквы были различны, то получили
бы ![]() новых "слов", но буква "М"
употребляется в
"слове" 2 раза, "А" - 3 раза, "Т" - 2 раза, оставшиеся три
буквы - по разу. Следовательно, искомое число будет в
новых "слов", но буква "М"
употребляется в
"слове" 2 раза, "А" - 3 раза, "Т" - 2 раза, оставшиеся три
буквы - по разу. Следовательно, искомое число будет в
![]() раз меньше, чем
раз меньше, чем ![]() ,
и равно
,
и равно
Число сочетаний с повторениями ![]() из
из ![]() элементов по
элементов по ![]() выражается через число сочетаний без
повторений:
выражается через число сочетаний без
повторений:
Пример 10. В кафе в продаже имеются 5 сортов пирожных. Сколькими способами 8 студенток могут заказать себе по одному пирожному?
Решение. Зашифруем каждую покупку 8 пирожных единицами по 5
сортам, разделяя сорта нулями. Тогда каждой покупке будет
соответствовать упорядоченный набор из 8 единиц и 4 (= 5 - 1)
разделительных нулей, а общее число покупок будет соответствовать
числу перестановок этих нулей и единиц ![]() .
Таким образом,
.
Таким образом,
Вопросы для самоконтроля
Задачи