Начало теории графов было положено Эйлером в 1736 году в его знаменитой задаче о кёнигсбергских мостах. Исследования электрических цепей, моделей кристаллов и структур молекул, развитие формальной логики побудили к изучению графов. Большое число популярных головоломок поддавалось формулировкам непосредственно в терминах графов. Проблема четырех красок - наиболее известная среди таких задач - была поставлена Де Морганом в 1850 году. В ХХ столетии теория графов получила дальнейшее развитие, которое связано с новыми ее приложениями: в теории игр и программировании, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем биологии и психологии.
В данной работе графы являются основой для иллюстрации основных результатов в теории вероятностей, что позволяет сделать рассматриваемый материал более наглядным и доступным.
Графом называется два множества с отношением инцидентности между их элементами, называемыми вершинами и ребрами. Это отношение удовлетворяет единственному требованию (аксиоме) - любое ребро инцидентно не более чем двум вершинам.
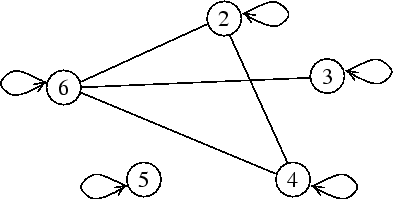
Пример 16. Построить граф, вершинами которого является множество {2, 3, 4, 5, 6}, а инцидентность задается наличием у указанных цифр делителей, отличных от единицы.
Решение. Взятые цифры обозначим на рисунке кружками, которые соединим отрезками (либо петлями) при наличии общих делителей.

Этот граф содержит 5 петель - ребра, соединяющие (инцидентные) вершину саму с собой. Вершина "5" - изолированная, а подграф с вершинами {2, 3, 4, 6} является связным. Граф связный, если из любой вершины в любую другую можно "пройти" по ребрам. Циклом называется замкнутый путь из ребер, например, вершины {2, 4, 6} с соединяющими их попарно ребрами. Степенью вершины называется число ребер графа, инцидентных этой вершине.
Пример 17. Сколько различных обедов П.И. Чичиков мог насчитать из блюд, выставленных на столе у П.П. Петуха, если бы на каждый обед выбирать только одно холодное блюдо, одно первое блюдо и одно второе блюдо? На столе у П.П. Петуха на этот раз были выставлены из холодных блюд студень с хреном, свежая икра, свежепросоленная белужина; на первое - уха из стерлядей, щи с грибами; на второе - осетрина жареная, теленок, жаренный на вертеле.
Решение. Каждое блюдо изобразим кружком с первой буквой названия блюда, а соответствие блюд одного обеда - отрезками, соединяющими кружки. Возникает схема (граф), изображенный на рисунке:
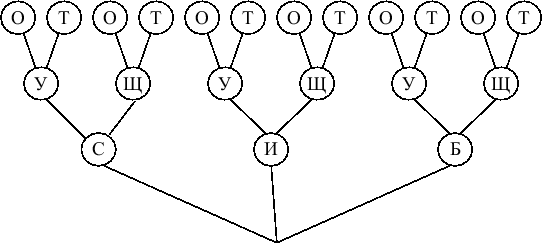
Граф помогает сосчитать число возможностей, их оказалось 12. Он же помогает узнать, сколько различных обедов можно составить, например, с икрой.
Математики, обратив внимание на сходство схемы на рисунке 2 с веткой дерева с листочками, назвали такие графы "деревьями".
Деревом называется связный граф без циклов. Очень важное понятие для нашего подхода к изложению теории вероятностей. При помощи дерева удобно изображать исходы того или иного испытания.
Пример 18. Поступающий на физмат должен сдать три вступительных экзамена по десятибалльной системе. Сколькими способами он может сдать экзамены, чтобы быть принятым в университет, если проходной балл в тот год составил 28 баллов?
Решение. Для решения этой задачи, как и во многих других комбинаторных и вероятностных задачах, эффективным оказывается организация элементов анализируемого множества в виде дерева. От одной выделенной вершины проводятся ребра, соответствующие оценке на первом экзамене, а затем к их концам добавляются новые ребра, соответствующие возможным результатам второго экзамена, а затем и третьего.
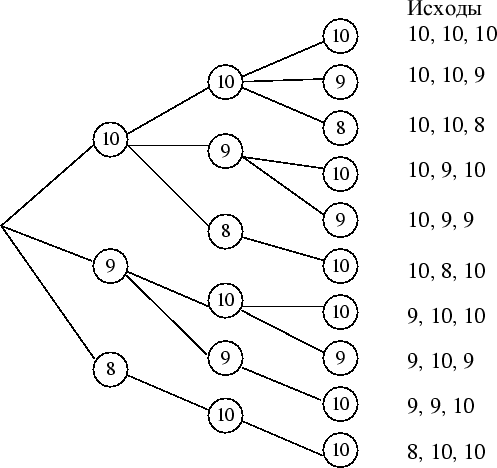
Таким образом, для поступления на физмат можно сдать вступительные экзамены 10 различными способами.
Из этого представления можно извлечь ряд идей, плодотворных для изучения комбинаторики и вероятности.
При рассмотрении цепей Маркова (далее §11) нам потребуются графы, на ребрах которых поставлены стрелки, указывающие на переход из одного состояния в другое. Ребро графа называется ориентированным, если одну вершину считают началом ребра, а другую - концом. Граф, все ребра которого ориентированы, называется ориентированным графом.
Пример 19. Турнир по волейболу проводится по круговой системе
между
![]() командами. Докажите, что если какие-нибудь две команды
одержали в турнире
одинаковое число побед, то найдутся среди участников три команды I, II
и III
такие, что I выиграла у II, II выиграла у III, a III выиграла у I.
командами. Докажите, что если какие-нибудь две команды
одержали в турнире
одинаковое число побед, то найдутся среди участников три команды I, II
и III
такие, что I выиграла у II, II выиграла у III, a III выиграла у I.
Решение. Пусть ![]() и
и ![]() -
две команды, одержавшие одинаковое
число побед, например,
-
две команды, одержавшие одинаковое
число побед, например, ![]() побед. Пусть к тому же
побед. Пусть к тому же ![]() выиграла у
выиграла у
![]() . Те
. Те ![]() команд, у которых выиграла
команда
команд, у которых выиграла
команда ![]() , обозначим
, обозначим
![]() ,
, ![]() , ...,
, ..., ![]() (рис. 4).
(рис. 4).
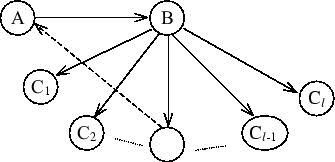
Команда ![]() не могла одержать победы над всеми
командами
не могла одержать победы над всеми
командами ![]() ,
,
![]() , ...,
, ..., ![]() , т.к. иначе она
одержала бы больше чем
, т.к. иначе она
одержала бы больше чем
![]() побед (одна победа над
побед (одна победа над ![]() уже имеется).
Следовательно, среди
команд
уже имеется).
Следовательно, среди
команд ![]() ,
, ![]() , ...,
, ..., ![]() найдется хотя бы одна,
которая одержала победу над
найдется хотя бы одна,
которая одержала победу над ![]() .
.
Из этого примера следует один из результатов теории графов о существовании ориентированных циклов в полном ориентированном графе.
Граф будет называться вероятностным, если рядом с каждым его ребром запишем соответствующую вероятность.
Пример 20. Построить вероятностное дерево исходов двух подбрасываний монеты на твердую поверхность.
Решение. Поскольку каждое подбрасывание монеты может закончиться одним из двух исходов, а именно, выпадением "герба" или "решки", то вероятностное дерево выглядит следующим образом:

Вопросы для самоконтроля
Задачи
а) всего было
передано четное число конвертов;
б) число студентов,
обменявшихся конвертами нечетное число раз,
четное.
а)
без единого поражения;
б) без
единой победы?