Далее: 2.  Описание установки Вверх: Методические указания Назад: Методические указания

1.  Краткая теория

Фотоэффект принадлежит к числу явлений, в которых обнаруживаются корпускулярные свойства света. Столкновение фотонов с электронами приводит к выбиванию электронов из фотокатода. Энергетический баланс этого взаимодействия устанавливается уравнениями Эйнштейна.

$$h\nu = E_{max}+A ,$$ (1)

где	$E_{max}$	-	максимальная кинетическая энергия
			освободившегося электрона.
	$A$	-	работа выхода электрона из фотокатода,
	$h$	-	постоянная Планка,
	$\nu$	-	частота света.

Произведение $h\nu$ определяет, как известно, энергию фотона для света с частотой $\nu$.

Даже при монохроматическом освещении энергия электронов, вылетающих из катода, оказывается неодинаковой. Электроны в веществе обладают разными энергиями, располагаясь по разрешенным энергетическим уровням разрешенных зон. Под работой выхода A понимают энергию, необходимую для удаления электрона с самых верхних энергетических уровней. Энергия, которую необходимо затратить, чтобы удалить электрон с ниже расположенных уровней, превосходит A, и кинетическая энергия таких электронов оказывается меньше. Кроме того, электроны могут терять часть своей энергии на пути к поверхности фотокатода. Соотношение (1) определяет поэтому кинетическую энергию не всех, а только наиболее быстрых фотоэлектронов.

При измерении энергии фотоэлектронов обычно пользуются методом задерживающего потенциала. Вблизи фотокатода располагается второй электрод (анод), к которому прикладывается отрицательный по отношению к катоду потенциал $U$. Как уже было сказано, вылетевшие из фотокатода электроны имеют различные энергии. Те электроны, энергия которых удовлетворяет условию $Е < еU$ ($е$ - заряд электрона), не могут достичь анода. Поэтому при увеличении $U$ анодный ток уменьшается. При некотором значении $U = U_{\text{з}}$ (потенциал запирания) даже наиболее быстрые фотоэлектроны не могут достичь анода, и анодный ток прекращается. Максимальная кинетическая энергия $Е_{мах}$ фотоэлектронов связана с задерживающим потенциалом соотношением:

$$E_{max} = e\cdot U_{\text{з}} .$$ (2)

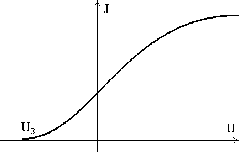
Рис. 1.1 

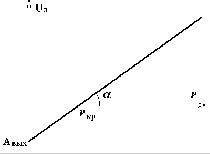
Рис. 1.2 

На опыте обычно изучается зависимость электронного тока в фотоэлементе от величины задерживающего потенциала $U_{\text{з}}$. Как следует из сказанного, форма кривой зависит от материала и толщины фотослоя. Она зависит, кроме того, от формы электродов и от условий освещения. Интерес представляет поэтому не сама кривая, а лишь точка пересечения кривой с осью $J=0$, определяющая потенциал запирания (рис. 1.1).

Подставляя (2) в (1), получаем

$h\nu = e U_{\text{з}}+A$

или окончательно

$$U_{\text{з}}={h \over e}\cdot\nu - {A\over e} .$$ (3)

Из уравнения (3) видно, что величина запирающего потенциала $U_{\text{з}}$ линейно зависит от частоты света (рис. 1.2).

При экспериментальной проверке уравнения Эйнштейна следует убедиться в том, что величина потенциала запирания $U_{\text{з}}$ зависит только от частоты света и притом линейно (рис. 1.2). По тангенсу угла $\alpha$ наклона прямой $U_{\text{з}}(\nu)$ к оси частот можно определить постоянную Планка:

$${\Delta U_{\text{з}} \over \Delta \nu}=\tg \alpha={dU_{\text{з}}\over d\nu} = {h \over e} .$$ (4)

(При этом следует иметь в виду, что $\tg\alpha$ в этом случае имеет физический смысл, и следовательно, является размерной величиной. Таким образом при расчете по графику величины ${\Delta U_{\text{з}}} \over {\Delta \nu}$ надо брать их в выбранных на графике единицах измерения.)

Таким образом, в расчетную формулу для определения не входит работа выхода $A$, что существенно упрощает проведение эксперимента. Тангенс угла наклона прямой к оси абсцисс можно определить по графику, либо аналитически с помощью метода наименьших квадратов.

Экспериментальная часть задания сводится к определению запирающего потенциала $U_{\text{з}}$. Точное определение этого потенциала наталкивается на ряд трудностей. Как показывает опыт, график $J=f(U_{\text{з}})$ (рис. 1.1) подходит к оси абсцисс под небольшим углом и даже заходит в область отрицательных значений $J$.

Значение запирающего потенциала становится несколько неопределенным. Такой ход кривой связан с наличием обратного фотоэффекта (т.е. фотоэффекта с анода) и с ионными токами в фотоэлементе из-за несовершенства вакуума. Поэтому следует проводить измерения $U_{\text{з}}$ несколько раз в каждой точке.

Далее: 2.  Описание установки Вверх: Методические указания Назад: Методические указания