Далее: 3. Описание установки Вверх: Лабораторная работа №6 Назад: 1. Вопросы для подготовки

2. Краткая теория

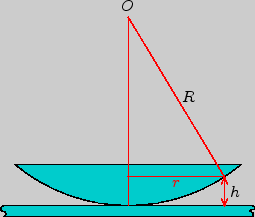
Классическим примером интерференционных полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис.2.1). (В принципе система может состоять и из двух линз с большим радиусом кривизны, причём не обязательно плоско-выпуклых). Роль тонкой плёнки, от поверхности которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой (или воздушный зазор между двумя линзами). Вследствие большой толщины пластинки и линзы и невысокой степени когерентности источника света не возникает интерференционной картины за счёт отражений от других поверхностей. При нормальном падении света полосы равной толщины имеет вид концентрических окружностей, при наклонном падении -- эллипсов.

$\includegraphics{lab_op4pic.1}$

Рис. 2.1

Рассмотрим схему возникновения и локализации колец Ньютона при наклонном падении света (рис.2.2а, б). Пусть -- небольшая часть нижней поверхности линзы, а -- верхняя поверхность стеклянной пластинки.

Рассмотрим луч света, падающий на поверхность воздушной прослойки. На поверхности в точке происходит частичное отражение и преломление луча. Таким образом, падающий луч разделился на два когерентных луча и .

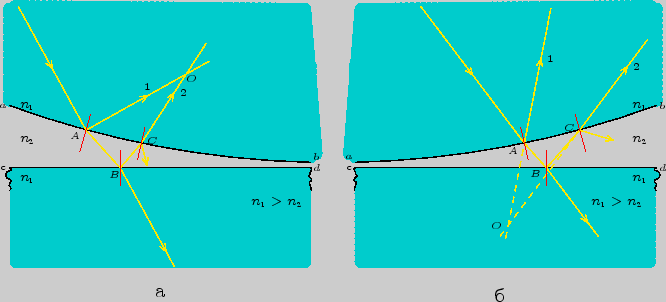
$\includegraphics{lab_op4pic.2}$

Рис. 2.2

Второй луч на поверхности в точке претерпевает аналогичный процесс разделения. Здесь нас интересует только отражённый луч. Ситуация повторяется и в точке , но здесь для нас важен преломлённый луч. В результате первый луч и часть второго встречаются над воздушной прослойкой (рис.2.2а), в точке , которая лежит на поверхности локализации интерференционной картины. В ситуации, показанной на рис.2.2б, полосы равной толщины локализуются под воздушной прослойкой.

При наклонном освещении системы ``линза - пластинка'' встречаются обе ситуации, поэтому понятно, что поверхность локализации интерференционной картины будет пересекать воздушную прослойку, т.е. будет несимметрична относительно оси системы (рис.2.1), которая является и осью наблюдения. Кроме того, расчёт разности хода лучей и в случае наклонного падения представляет собой довольно громоздкую геометрическую задачу.

Эти трудности можно обойти, если рассмотреть лучи, падающие нормально к поверхности плоскопараллельной пластинки (Следует обратить внимание на то, что на плоскую поверхность линзы в этом случае должен падать не строго параллельный пучок света, а слабо расходящийся.) В этом случае поверхность локализации совпадает с нижней (сферической) поверхностью линзы, т.е. является симметричной оси наблюдения и разность хода вычисляется очень просто (см. ниже).

Найдём радиусы колец Ньютона, получающиеся при падении света нормально к верхней (плоской) поверхности линзы (а не к поверхности пластинки!), т.к. это существенно проще практически сделать. При вычислении разности хода мы должны пренебречь в этом случае небольшими неизбежными наклонами лучей, проходящих в воздушном зазоре. (Т.е. падение лучей к поверхности плоскопараллельной пластинки будет несколько не перпендикулярным, но эксперимент при этом облегчается существенно.)

Оптическая разность хода $\Delta$ в этом случае равна удвоенной толщине воздушного зазора (см. рис.2.1; предполагается, что ). Как следует из рис.2.1,

$\begin{displaymath} r^2 = R^2-(R-h)^2=2Rh-h^2\,, \end{displaymath}$

(1)

где		--	радиус кривизны выпуклой поверхности линзы,
		--	радиус окружности, всем точкам которой соответствует одинаковый зазор .

Принимая во внимание, что $2R\gg h$ , получим

$\begin{displaymath} h\approx{r^2\over2R}\,. \end{displaymath}$

(2)

Известно, что cвет, отражённый от границы стекло-воздух по сравнению со светом, отражённым от границы воздух-стекло приобретает дополнительный фазовый сдвиг на $\pi$ , что соответствует разности хода $\lambda\over 2$ . Полная разность хода, таким образом, равна: