Далее: 12.  Задачи для самостоятельного Вверх: 11.  Электромагнетизм Назад: 11.  Электромагнетизм

1.  Примеры решения задач

Пример 11.9. Между полюсами магнита на двух тонких вертикальных npоволочках подвешен горизонтальный линейный проводник массой $\displaystyle{m=10\,{\text{г}}}$ и длиной $\displaystyle{\ell=20\,{\text{см}}}$ . Индукция однородного магнитного поля направлена вертикально и равна $\displaystyle{\vec{B}=0,25\,{\text{Тл}}}$ . Весь проводник находится в магнитном поле. На какой угол от вертикали отклоняются проволочки, поддерживающие проводник, если по нему пропустить ток силой $\displaystyle{I=2\,A}$ ? Массами проволочек пренебречь.

Дано:
$\displaystyle{m=0,01\,{\text{кг}}}$
$\displaystyle{\ell=0,2\,{\text{м}}}$
$\displaystyle{B=0,25\,{\text{Тл}}}$
$\displaystyle{I=2\,A}$
 
$\displaystyle{\alpha}$ – ?

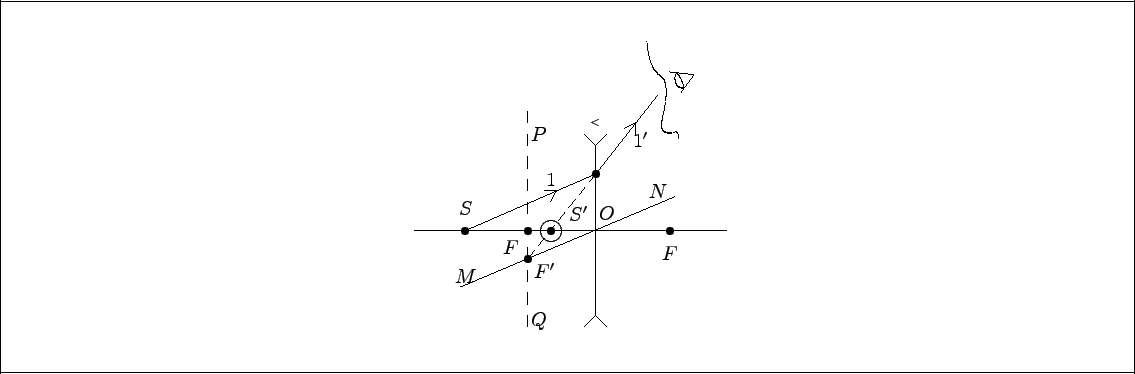
Решение. На проводник с током в магнитном поле действует сила Ампера, которая отклонит проволочки, поддерживающие проводник, от вертикали. Для наглядности решения задачи изобразим проводник в таком положении, что ток в нем уходит за плоскость листа, при этом линии магнитной индукции направим вертикально вверх ( $\displaystyle{AC}$ – одна из проволок, поддерживающих проводник).

\begin{picture}(56.00,51.33) \emline{33.00}{33.00}{1}{33.00}{3.00}{2} \emline{31... ...1}{31.20}{25.75}{62} \emline{31.79}{26.49}{63}{33.00}{28.00}{64} \ \end{picture}

Рис. 11.1 

Будем считать, что все силы, действующие на проводник, приложены в центре тяжести проводника.

Напишем условие равновесия линейного проводника, подвешенного на вертикальных проволоках $\displaystyle{AC}$ , в магнитном поле после пропускания тока:

\begin{equation} m\vec{g} + \vec{F_A}+\vec{T}=0\,, \end{equation}
  (65)

здесь $\displaystyle{\vec{T}}$ – суммарная сила натяжения поддерживающих проволочек;
  $\displaystyle{\vec{F}_A}$ – сила Ампера, направление которой определяется по правилу левой руки.

Спроектируем уравнение (65) на оси $\displaystyle{OX}$ и $\displaystyle{OY}$ :

\begin{eqnarray} F_A-T\sin{\alpha}&=& {0} \,,\\ -mg+T\cos{\alpha}&=& {0} \nonumber \end{eqnarray}
      (66)
       

Перепишем систему (66) в виде:

\begin{equation} F_A=T\sin{\alpha}\,, \end{equation}
  (67)

\begin{equation} mg=T\cos{\alpha}\,. \end{equation}
  (68)

После деления выражения (67) на (68) получим:

\begin{equation} {F_A\over mg}={\mbox{tg}\,}\,. \end{equation}
  (69)

Учтем, что сила Ампера $\displaystyle{F_A=IB\ell\sin{\beta}}$ . По условию задачи $\displaystyle{\beta=90^\circ\,,\ \sin{\beta}=1}$ . Подставив данные в уравнение (69), рассчитаем угол, на который отклоняются проволочки, поддерживающие проводник с током в магнитном поле:

\begin{equation} {\mbox{tg}\,}={IB\ell\over mg}\,;\quad {\mbox{tg}\,}={2\cdot 0,25\cdot 0,2\over 0,01\cdot 9,8}=1\,,\quad \alpha=45^\circ\,. \end{equation}
  (70)

Проверим единицы измерения:

\begin{equation} [{\mbox{tg}\,}]={A\cdot{\text{Тл}}\cdot{\text{м}}\over{\text{кг}} \cdot{{\text{Н}}\over{\text{кг}}}}={A\cdot{\text{Н}}\cdot{\text{м}}\over A\cdot{\text{м}}\cdot{\text{Н}}}\ - {\text{величина безразмерная.}} \end{equation}
  (71)

Ответ: $\displaystyle{\alpha=45^\circ С\,}$ .

Пример 11.10. На проволочный виток радиусом 10см, помещенный между полюсами магнита, действует максимальный механический момент 6,5мкНм. Сила тока в витке равна 2А. Определить магнитную индукцию поля между полюсами магнита. Действием магнитного поля Земли пренебречь.

Дано:
$\displaystyle{r=10\,{\text{см}}=0,1\,{\text{м}}}$
$\displaystyle{{\text{М}}_{max}=6,5\cdot 10^{-6}\, {\text{H}}\cdot{\text{м}}}$
$\displaystyle{I=2\,A}$
 
$\displaystyle{B}$ - ?

Решение. На контур с током (виток или рамку), помещенный в магнитное поле, действует вращательный момент, который определяется так:

\begin{equation} \vec{M}=\vec{p}_m\times\vec{B}\,, \end{equation}
  (72)

где $\displaystyle{\vec{p}_m}$ - магнитный момент контура с током

\begin{equation} \vec{p}_m={p}_m\vec{n}\,;\quad {p}_m=IS\,, \end{equation}
  (73)

$\displaystyle{\vec{n}}$ – единичный вектор, направление которого совпадает с направлением положительной нормали. Таким образом, контур с током в магнитном поле будет поворачиваться до тех пор, пока вектор $\displaystyle{\vec{n}}$ не совпадет с направлением $\displaystyle{\vec{B}}$ , то есть контур с током в магнитном поле ориентируется. Перепишем выражение (72):

\begin{equation} M={p}_mB\sin{\alpha}\,. \end{equation}
  (74)

По условию задачи на проволочный виток действует максимальный механический момент. Следовательно, угол $\displaystyle{\alpha}$ между $\displaystyle{\vec{p}}$ и $\displaystyle{\vec{B}}$ составляет $\displaystyle{90^\circ}$ и $\displaystyle{\sin{\alpha}=1}$ . Если учесть (73), выражение (74) можно записать так: $\displaystyle{M_{max}=ISB}$ , здесь $\displaystyle{S}$ – площадь контура радиусом 10см, то есть $\displaystyle{S=\pi r^2}$ . Запишем окончательное выражение для определения искомого вектора В:

\begin{equation} B={M_{max}\over I\pi r^2}\,. \end{equation}
  (75)

Произведем расчет:

\begin{equation} B={6,5\cdot 10^{-6}\over 2\cdot 3,14\cdot 0,01}\,{\text{Тл}}=103,5\cdot 10^{-6}\,{\text{Тл}}=103,5\,{\text{мкТл}}\,. \end{equation}
  (76)

Проверим единицы измерения:

\begin{equation} [B]={{\text{Н}}\cdot{\text{м}}\over A\cdot{\text{м}}^2}= {{\text{Н}}\over A\cdot{\text{м}}}={\text{Тл}}\,. \end{equation}
  (77)

Ответ: $\displaystyle{B=103,5\,{\text{мкТл}}\,.}$

Пример 11.11. Электрон, пройдя ускоряющую разность потенциалов 400В, попал в однородное магнитное поле с индукцией 1,5мТл. Определить: 1) радиус кривизны траектории; 2) частоту вращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

Дано:
$\displaystyle{U=400\,B}$
$\displaystyle{B=1,5\cdot 10^{-3}\,{\text{Тл}}}$
$\displaystyle{\vec{v}\bot\vec{B}}$
$\displaystyle{e=1,6\cdot 10^{-19}\,{\text{Кл}}}$
$\displaystyle{m=9,1\cdot 10^{-31}\,{\text{кг}}}$
 
1) $\displaystyle{R}$ - ? 2) $\displaystyle{n}$ - ?

Решение. 1) На заряд, движущийся со скоростью $\displaystyle{\vec{v}}$ в магнитном поле с индукцией $\displaystyle{\vec{B}}$ , действует сила Лоренца $\displaystyle{\vec{F}=q|\vec{v}\times\vec{B}|}$ или $\displaystyle{F = |e|\vec{v}B\sin{\alpha}}$ . Вектор силы Лоренца перпендикулярен вектору скорости $\displaystyle{\vec{v}}$ и, следовательно, сообщает электрону нормальное ускорение. Учитывая это, можно записать:

\begin{equation} |e|vB\sin{\alpha}=m{v^2\over R}\,. \end{equation}
  (78)

Из формулы (78) выразим радиус кривизны траектории, принимая во внимание, что $\displaystyle{\alpha=90^\circ}$ по условию:

\begin{equation} R={mv\over |e|B}\,. \end{equation}
  (79)

Входящую в выражение (79) скорость электрона выразим через кинетическую энергию электрона:

\begin{equation} E={mv^2\over 2}\,. \end{equation}
  (80)

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов $\displaystyle{U}$ , определяется равенством: $\displaystyle{E_{{\text{к}}}=|e|U}$ . Подставим это выражение в формулу (80) и выразим скорость электрона:

\begin{equation} v=\sqrt{2|e|U\over m}\,. \end{equation}
  (81)

Вернемся к выражению (79) с учетом скорости

\begin{equation} R={m\over |e|B}\sqrt{2|e|U\over m}={1\over B}\sqrt{2mU\over |e|}\,. \end{equation}
  (82)

Произведем вычисления:

\begin{equation} R={1\over 1,5\cdot 10^{-3}}\sqrt{2\cdot 9,1\cdot 10^{-31}\cdot 400\over 1,6\cdot 10^{-19}}\,{\text{м}}=4,5\cdot 10^{-2}\,{\text{м}}=4,5\,{\text{см}}\,. \end{equation}
  (83)

Проверим единицы измерения:

\begin{equation} [R]={1\over{\text{Тл}}}\sqrt{{\text{кг}}\cdot B\over {\text{Кл}}}={A\cdot{\text{м}}\over{\text{Н}}}\sqrt{{\text{кг}}\cdot B\over A \cdot c}={\text{м}}\sqrt{A\cdot{\text{кг}}\cdot B\over {\text{Н}}^2\cdot{\text{с}}}={\text{м}}\sqrt{{\text{Дж}}\cdot{\text{кг}}\over {\text{Н}}^2\cdot{\text{с}}^2}= {\text{м}}\sqrt{{\text{Дж}}\cdot{\text{кг}}\cdot{\text{м}}^2\over {\text{Дж}}^2\cdot{\text{с}}^2}={\text{м}}\,. \end{equation}
  (84)

2) Для определения частоты вращения электрона воспользуемся соотношением между линейной скоростью движения электрона и угловой скоростью:

\begin{equation} v=\omega R=2\pi nR\,,\quad{\text{откуда}} \end{equation}
  (85)

\begin{equation} n={v\over 2\pi R}={|e|B\over 2\pi m}\,. \end{equation}
  (86)

\begin{equation} n={1,6\cdot 10^{-19}\cdot 1,5\cdot 10^{-3}\over 2\cdot 3,14\cdot 9,1\cdot10^ {-31}}=4,2\cdot 10^7\,{\text{с}}^{-1}=4,2\cdot 10^7\,{\text{Гц}}\,. \end{equation}
  (87)

Ответ: $\displaystyle{R=4,5\,{\text{см}}\,;\ n=4,2\cdot 10^7\,{\text{Гц}}\,.}$

Далее: 12.  Задачи для самостоятельного Вверх: 11.  Электромагнетизм Назад: 11.  Электромагнетизм

ЯГПУ, Отдел образовательных информационных технологий 10.07.2012