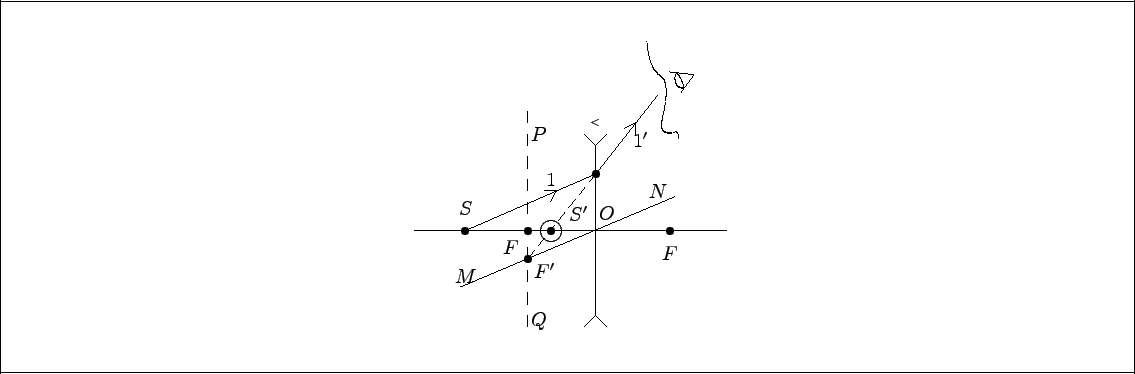
Пример 14.12. Построить изображение произвольной точки $\displaystyle{S}$ , которая лежит на главной оптической оси рассеивающей линзы.

Рис. 14.1 [ $\displaystyle{S}$ – светящаяся точка Л – рассеивающая линза $\displaystyle{OF}$ – aглавная оптическая ось $\displaystyle{F}$ – главные фокусы линзы ]
Решение. Фокусы рассеивающей линзы мнимые, то есть в них собираются не лучи, а их продолжения. Для того, чтобы получить изображение точки $\displaystyle{S}$ линзой Л, возьмем любой луч 1, падающий из точки $\displaystyle{S}$ на линзу. Затем найдем точку пересечения побочной оптической оси (прямая $\displaystyle{MN}$ , параллельная лучу 1, проходящая через оптический центр $\displaystyle{O}$ ) и сечения фокальной плоскости (прямая $\displaystyle{PQ}$ , проходящая через главный фокус, перпендикулярная главной оптической оси). $\displaystyle{F'}$ – мнимый побочный фокус – точка, в которой собираются продолжения всех лучей рассеянных линзой, если они падают на нее параллельно лучу 1. Следовательно, через эту точку пройдет продолжение луча $\displaystyle{1'}$ . На пересечении его с главной оптической осью получается изображение точки $\displaystyle{S - S'}$ .Ответ: Изображение точки $\displaystyle{S}$ – точка $\displaystyle{S'}$ . Это мнимое изображение источника. Его нельзя получить на экране, но можно увидеть глазом, если смотреть сквозь линзу в направлении луча $\displaystyle{1'}$ .
Пример 14.13. Свет от монохроматического источника ( $\displaystyle{\lambda=600\,{\text{нм}}}$ ) падает нормально на диафрагму с круглым отверстием диаметром 6мм. За диафрагмой на расстоянии 3м от нее находится экран, на котором наблюдается дифракционная картина. Определить, темным или светлым будет центр дифракционной картины на экране.
Дано:
| |||
| $\displaystyle{m}$ – ? |
Решение.
Диафрагма – это оптическое устройство для ограничения или изменения светового пучка. Свет испытывает дифракцию на круглом отверстии диафрагмы (Д) и попадает на экран (Э) (см.рис. 14.2).
Основная задача дифракции состоит в расчете распределения интенсивности дифрагировавшего света. Это можно сделать, использовав принцип Гюйгенса - Френеля. Согласно принципу Гюйгенса, каждая точка фронта волны является самостоятельным источником вторичных волн. Эти волны интерферируют, и результат их интереференции определяет интенсивность света в той или иной точке. Для решения этой задачи Френель предложил разбить фронт волны на зоны так, чтобы расстояния от краев двух соседних зон отличались на половину длины волны – $\displaystyle{{\lambda\over 2}}$
(см. рис. 14.2, $\displaystyle{ b_1=b+{\lambda\over 2}\,; \quad b_2=b_1+{\lambda\over 2}=b+2{\lambda\over 2}\,;\quad b_3=b_2+{\lambda\over 2}=b+3{\lambda\over 2}\,;\ \ldots\ b_m=b+m{\lambda\over 2}}$ ).
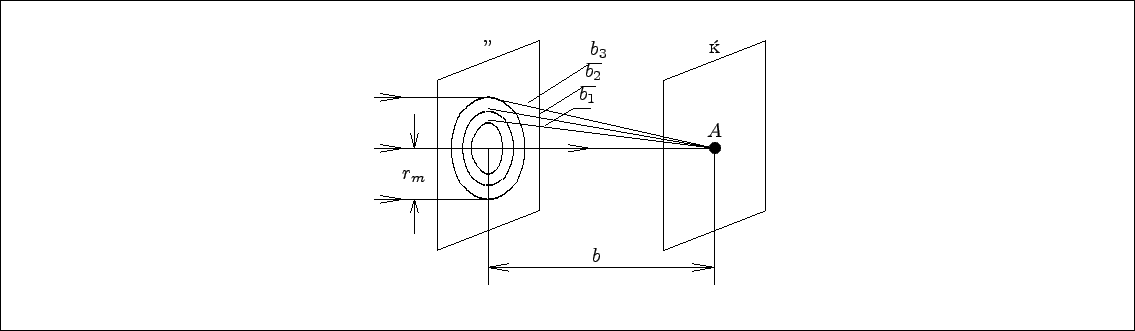
Рис. 14.2
При разности хода $\displaystyle{\lambda\over 2}$ волны от соседних зон приходят в точку наблюдения в противофазе и ослабляют друг друга. Таким образом, если на открытом фронте волны (в нашем случае в отверстии диафрагмы) укладывается четное число зон Френеля, в точке наблюдения – минимум интенсивности, если в отверстии укладывается нечетное число зон Френеля, в точке наблюдения – максимум интенсивности, причем наибольшая интенсивность будет, если в отверстии укладывается одна зона Френеля, наименьшая, если – две.Для расчета числа зон Френеля, укладывающихся в отверстии диафрагмы, используем формулу для расчета радиуса зоны Френеля с номером m:
| (88) |
где $\displaystyle{a}$ и $\displaystyle{b}$ соответственно расстояния диафрагмы от источника и от экрана.
В условии задачи сказано, что свет падает на диафрагму нормально. Это возможно, если источник находится достаточно далеко, то есть $\displaystyle{a}$ следует принять равным $\displaystyle{\infty}$ .
Выразим $\displaystyle{m}$ :
| (89) |
Принимая во внимание, что $\displaystyle{a=\infty}$ , получим
| (90) |
Вычисления.
| (91) |
Ответ: В отверстии диафрагмы из точки наблюдения ( $\displaystyle{A}$ ) укладывается 5 зон Френеля, значит центр дифракционной картины будет светлым.
Пример 14.14. При облучении фотокатода видимым светом задерживающая разность потенциалов оказалась равной 1,2В. Минимальная длина волны, применявшаяся в опыте, равно 400нм. Определить красную границу фотоэффекта.
| Дано: $\displaystyle{U_{{\text{з}}}=1,2\,B}$ $\displaystyle{\lambda_{min}=400\,{\text{нм}}=4\cdot 10^{-7}\,{\text{м}}}$ |
| $\displaystyle{\lambda_o}$ - ? |
Решение. Внешний фотоэффект – это выбивание электронов из металла при облучении его светом. Красная граница фотоэффекта – максимальная длина волны ( $\displaystyle{\lambda_o}$ ), которой соответствует минимальная частота ( $\displaystyle{\nu_o}$ ). При облучении металла фотонами меньшей частоты фотоэффект не наблюдается.
Наличие красной границы фотоэффекта может быть объяснено из уравнения Эйнштейна для фотоэффекта:
| (92) |
Задерживающая разность потенциалов – это обратное напряжение, которое нужно приложить между фотокатодом и анодом, чтобы фототок прекратился, то есть
| (93) |
Используя уравнение Эйнштейна и учитывая, что $\displaystyle{\nu={c\over \lambda}}$ , получим:
| (94) |
| (95) |
| (96) |
Проверка единицы измерения искомой величины:
| (97) |
Наименование м соответствует единице измерения длины волны. Выражение для длины волны в общем виде получено верно.
Вычисления:
| (98) |
Ответ: Максимальная длина волны, при которой будет существовать фотоэффект с данного фотокатода (красная граница), равна $\displaystyle{6,5\cdot 10^{-7}\,{\text{м}}\,}$ . Это соответствует красной части спектра видимого света.
ЯГПУ, Отдел образовательных информационных технологий 10.07.2012