Далее: Описание этапов проведения лабораторной Вверх: Лабораторная работа № 3 Назад: Лабораторная работа № 3

Теоретический аспект

При вычислениях значений определенных интегралов нередко встречаются следующие проблемы:

Невозможность или сложность выражения подынтегральной функции через элементарные функции.

Аналитическое задание подынтегральной функции в виде таблицы значений функции в зависимости от аргумента.

Графическое задание подынтегральной функции с использованием соответствующего графика значений функции в зависимости от аргумента.

В подобных ситуациях для вычисления приближенных значений определенных интегралов используются численные методы.

Согласно методу механических квадратур, подынтегральную функцию $y = f\left( x \right)$ можно заменить интерполяционным многочленом степени "S" в силу приближенных вычислений значений функции $y = f\left( x \right)$:

$$P_S \left( x \right) = a_S x^S + a_{S - 1} x^{S - 1} + ... +... ...t( {x_i } \right) = y_i ,\qquad\mbox{где}\qquad i = 0,1,...,N.$$

Геометрическая интерпретация метода заключается в том, что график исходной функции $y = f\left( x \right)$ заменяется "параболой степени "S"" $y = f\left( x \right) = P_S \left( x \right) = a_S x^S + a_{S - 1} x^{S - 1} + ... + a_2 x^2 + a_1 x + a_0$, проходящей через $''S + 1''$ точек графика данной функции.

В данной лабораторной работе интерполяционный многочлен степени "S" представляется в следующем виде:

$$P_S \left( x \right) = a_0 + a_1 \cdot \left( {x - x_0 } \ri... ...x_0 } \right) \cdot ... \cdot \left( {x - x_{n - 1} } \right).$$

Приближенное значение определенного интеграла от подынтегральной функции $y = f\left( x \right)$ на заданном отрезке $\left[ {a_0 ,b_0 } \right]$ равно значению определенного интеграла от интерполяционного многочлена на заданном отрезке $\left[ {a_0 ,b_0 } \right]$, при этом осуществляется деление данного отрезка на определенное количество равных меньших отрезков или шагов в зависимости от заданного значения количества шагов $s_\alpha$ или значения фиксированного шага $h_\alpha$, осуществляется расчет приближенного значения определенного интеграла на каждом из полученных отрезков с последующим нахождением приближенного значения определенного интеграла на заданном отрезке $\left[ {a_0 ,b_0 } \right]$ как суммы найденных приближенных значений определенных интегралов на каждом из равных меньших отрезков.

Таким образом, рассматриваемые в рамках данной лабораторной работы численные методы используются для приближенных вычислений определенных интегралов от подынтегральных функций $f(x)$ на отрезке $[a_0 ,b_0 ]$ в зависимости от заданного значения количества шагов $s_\alpha$ или значения фиксированного шага $h_\alpha$.

Рассмотрим логические основы реализации расчетов по формулам средних прямоугольников, трапеций, параболических трапеций (Симпсона) (замена подынтегральной функции интерполяционными многочленами нулевой, первой и второй степеней соответственно) для вычислений приближенных значений определенных интегралов в зависимости от различных значений $a_0$, $b_0$, $s_\alpha$ или $h_\alpha$, заложенных в программу "APROXINT".

Формула средних прямоугольников

Замена подынтегральной функции интерполяционным многочленом нулевой степени на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ].$

Имеем одно заданное значение подынтегральной функции $y_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} = ... ...athord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right)$ при $x = x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$.

Тогда $P_0 \left( x \right) = f\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right) = a_0$ и $y = f\left( x \right) \approx P_0 \left( x \right) = f\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right)$.

В данном случае график подынтегральной функции $y = f\left( x \right)$ на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ]$ заменяется горизонтальной прямой, проходящей через точку с координатами $\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspac... ...{x_0 + \frac{h_\alpha }{2},f\left( {x_0 + \frac{h_\alpha }{2}} \right)} \right)$.

Вычисление приближенного значения определенного интеграла на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ].$

$$\begin{array}{l} \int\limits_{x_0 }^{x_{_1 } } {f\left( x \... ...ight. \kern-\nulldelimiterspace} 2} } \right). \\ \end{array}$$

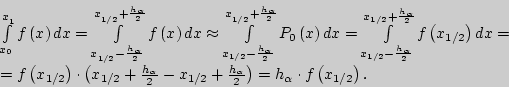
Таким образом, приближенное значение определенного интеграла на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ]$ равно площади прямоугольника со значениями стороны $f\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right)$ и высоты $h_\alpha$.

Вычисление приближенного значения определенного интеграла по формуле средних прямоугольников на отрезке $[a_0 ,b_0 ].$

$$\int\limits_{x_0 }^{x_1 } {f\left( x \right)dx} \approx h_\a... ...hantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right).$$

$$\begin{array}{l} \int\limits_{x_0 }^{x_2 } {f\left( x \righ... ...rn-\nulldelimiterspace} 2} } \right)} \right). \\ \end{array}$$

$$\begin{array}{l} \int\limits_{x_0 }^{x_3 } {f\left( x \righ... ...rn-\nulldelimiterspace} 2} } \right)} \right). \\ \end{array}$$

................................. ................................. .............................

$$\int\limits_{x_0 }^{x_N } {f\left( x \right)dx} = \sum\limit... ...}} \right. \kern-\nulldelimiterspace} 2} } \right)} \right)} .$$

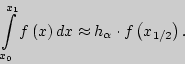
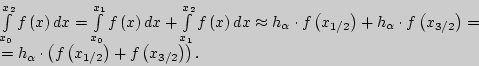
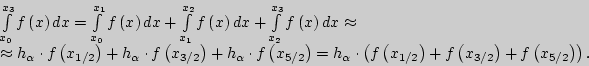
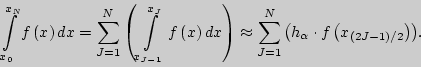
Тогда приближенное значение определенного интеграла на отрезке $[a_0 ,b_0 ]$ определяется согласно следующему соотношению:

$$\int\limits_{a_0 }^{b_0 } {f\left( x \right)dx} = \int\limit... ...}} \right. \kern-\nulldelimiterspace} 2} } \right)} \right)} .$$

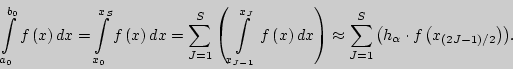
В данной лабораторной работе использование формулы средних прямоугольников ("FORMULA OF MIDDLE RECTANGLES") имеет следующую реализацию:

Итерация с индексом $''N'' \quad \left( {N \ge 1} \right)$:

На отрезке $\left[ {a_0 ,b_0 } \right]$ при соблюдении условия $a_0 < b_0$, исходя из вводимого или рассчитанного значения фиксированного шага $h_\alpha ^{MR}$ (при вводимом значении количества шагов $s_\alpha ^{MR}$ по формуле $h_\alpha ^{MR} = \frac{b_0 - a_0 }{s_\alpha ^{MR} })$ выбирается абсцисса точки подынтегральной функции с координатами $\left( {x_N^{MR} ,f\left( {x_N^{MR} } \right)} \right)$, то есть $x_N^{MR}$ согласно следующему соотношению: $x_N^{MR} = x_{N - 1}^{MR} + h_\alpha ^{MR}$.

Осуществляется вычисление площади элементарного прямоугольника $q_N^{MR}$, значение высоты которого $h_\alpha ^{MR} = x_N^{MR} - x_{N - 1}^{MR} = x_1^{MR} - x_0^{MR}$, согласно следующему соотношению: $q_N^{MR} = h_\alpha ^{MR} \cdot f\left( {x_{{\left( {2N - 1} \right)} \mathord{... ...eft( {2N - 1} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}^{MR} } \right)$.

Осуществляется вычисление приближенного значения определенного интеграла на отрезке $\left[ {a_0 ,x_N^{MR} } \right]$ согласно следующему соотношению: $I_{\alpha N}^{MR} = I_{\alpha \left( {N - 1} \right)}^{MR} + q_N^{MR}$.

Если достигнута истинность выражения $x_N^{MR} \ge b_0$, то итерации прекращаются, количество шагов итераций $s_\alpha ^{MR} = N$, и приближенное значение определенного интеграла $I_\alpha ^{MR} = I_{\alpha N}^{MR}$.

Если $x_N^{MR} < b_0$, то осуществляется переход к следующей итерации.

Формула трапеций

Замена подынтегральной функции интерполяционным многочленом первой степени на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ].$

Имеем два заданных значения подынтегральной функции $y_0 = f\left( {x_0 } \right)$ при $x = x_0$ и $y_1 = f\left( {x_0 + h_\alpha } \right)$ при $x = x_1 = x_0 + h_\alpha$.

Тогда $P_1 \left( x \right) = f\left( {x_1 } \right) = a_0 + a_1 \cdot \left( {x_1 - x... ...htarrow a_1 = \frac{f\left( {x_1 } \right) - f\left( {x_0 } \right)}{h_\alpha }$ и $y = f\left( x \right) \approx P_1 \left( x \right) = f\left( {x_0 } \right) + \... ... } \right) - f\left( {x_0 } \right)}{h_\alpha } \cdot \left( {x - x_0 } \right)$.

В данном случае график подынтегральной функции $y = f\left( x \right)$ на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ]$ заменяется наклонной прямой, проходящей через точки $\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspac... ...eft/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right)} \right)$ и $\left( {x_1 ,f\left( {x_1 } \right)} \right) = \left( {x_0 + h_\alpha ,f\left( {x_0 + h_\alpha } \right)} \right)$.

Вычисление приближенного значения определенного интеграла на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ].$

$$\int\limits_{x_0 }^{x_1 } {f\left( x \right)dx} = \int\limit... ...ight)}{h_\alpha } \cdot \left( {x - x_0 } \right)} \right)dx}.$$

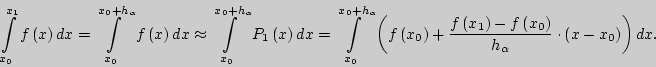
Выполним замену переменной:

$$t = \frac{x - x_0 }{h_\alpha }, \quad x = x_0 + t \cdot h_\alpha , \quad dx = h_\alpha dt.$$

$$x = x_0 \Rightarrow t = 0, \quad x = x_1 = x_0 + h_\alpha \Rightarrow t = 1.$$

Тогда

$$\begin{array}{l} \int\limits_{x_0 }^{x_0 + h_\alpha } {\lef... ...( {x_0 } \right) + f\left( {x_1 } \right)}{2}. \\ \end{array}$$

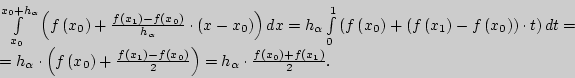
В итоге имеем:

$$\int\limits_{x_0 }^{x_1 } {f\left( x \right)dx} \approx h_\a... ...dot \frac{f\left( {x_0 } \right) + f\left( {x_1 } \right)}{2}.$$

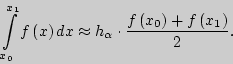
Таким образом, приближенное значение определенного интеграла на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ]$ равно площади прямоугольной трапеции со значениями оснований $f\left( {x_0 } \right)$, $f\left( {x_1 } \right)$ и высотой $h_\alpha$.

Вычисление приближенного значения определенного интеграла по формуле трапеций на отрезке $[a_0 ,b_0 ].$

$$\int\limits_{x_0 }^{x_1 } {f\left( x \right)dx} \approx h_\a... ...dot \frac{f\left( {x_0 } \right) + f\left( {x_1 } \right)}{2}.$$

$$\begin{array}{l} \int\limits_{x_0 }^{x_2 } {f\left( x \righ... ...\right)}{2} + f\left( {x_1 } \right)} \right). \\ \end{array}$$

$$\begin{array}{l} \int\limits_{x_0 }^{x_3 } {f\left( x \righ... ...1 } \right) + f\left( {x_2 } \right)} \right). \\ \end{array}$$
................................. ................................. .............................

$$\int\limits_{x_0 }^{x_N } {f\left( x \right)dx} = \sum\limit... ...sum\limits_{J = 1}^{N - 1} {f\left( {x_J } \right)} } \right).$$

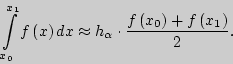
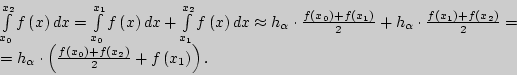
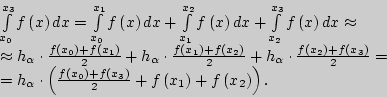
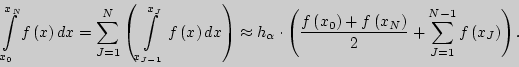
Тогда приближенное значение определенного интеграла на отрезке $[a_0 ,b_0 ]$ определяется согласно следующему соотношению:

$$\begin{array}{l} \int\limits_{a_0 }^{b_0 } {f\left( x \righ... ... 1}^{S - 1} {f\left( {x_J } \right)} } \right) \\ \end{array}$$

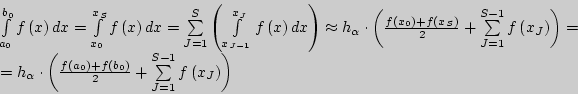
В данной лабораторной работе использование формулы трапеций ("FORMULA OF TRAPEZOIDS") имеет следующую реализацию:

Итерация с индексом "N" $\left( {N \ge 1} \right)$:

На искомом отрезке $\left[ {a_0 ,b_0 } \right]$ при соблюдении условия $a_0 < b_0$, исходя из вводимого или рассчитанного значения фиксированного шага $h_\alpha ^T$ (при вводимом значении количества шагов $s_\alpha ^T$ по формуле $h_\alpha ^T = \frac{b_0 - a_0 }{s_\alpha ^T })$, выбирается абсцисса точки подынтегральной функции с координатами $\left( {x_N^T ,f\left( {x_N^T } \right)} \right)$, то есть $x_N^T$ согласно следующему соотношению: $x_N^T = x_{N - 1}^T + h_\alpha ^T$.

Осуществляется расчет площади элементарной прямоугольной трапеции $q_N^T$, значение высоты которой $h_\alpha ^T = x_N^T - x_{N - 1}^T = x_1^T - x_0^T$, согласно следующему соотношению: $q_N^T = h_\alpha ^T \cdot \frac{f\left( {x_{N - 1}^T } \right) + f\left( {x_N^T } \right)}{2}$.

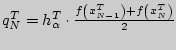Осуществляется расчет приближенного значения определенного интеграла на отрезке $\left[ {a_0 ,x_N^T } \right]$ согласно следующему соотношению: $I_{\alpha N}^T = I_{\alpha \left( {N - 1} \right)}^T + q_N^T$.

Если достигнута истинность выражения $x_N^T \ge b_0$, то итерации прекращаются, количество шагов итераций $s_\alpha ^T = N$, и приближенное значение определенного интеграла $I_\alpha ^T = I_{\alpha N}^T$.

Если $x_N^T < b_0$, то осуществляется переход к следующей итерации.

Формула параболических трапеций (Симпсона)

Замена подынтегральной функции интерполяционным многочленом второй степени на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ].$

Имеем три заданных значения подынтегральной функции $y_0 = f\left( {x_0 } \right)$ при $x = x_0$, $y_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} = ... ...left/ {\vphantom {{h_\alpha } 2}} \right. \kern-\nulldelimiterspace} 2} \right)$ при $x = x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2... ...mathord{\left/ {\vphantom {{h_\alpha } 2}} \right. \kern-\nulldelimiterspace} 2$ и $y_1 = f\left( {x_0 + h_\alpha } \right)$ при $x = x_1 = x_0 + h_\alpha$.

Тогда

$$\begin{array}{l} P_2 \left( x \right) = a_0 + a_1 \cdot \le... ... \frac{h_\alpha }{2} = f\left( {x_1 } \right). \\ \end{array}$$

$$f\left( {x_0 } \right) + 2\left( {f\left( {x_{1 \mathord{\le... ...\left( {x_0 } \right)} \right)}{\left( {h_\alpha } \right)^2}.$$

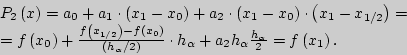
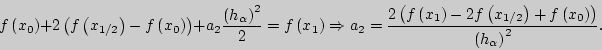
Получим, что

$$\begin{array}{l} y = f\left( x \right) \approx P_2 \left( x... ... {x_0 + \frac{h_\alpha }{2}} \right)} \right). \\ \end{array}$$

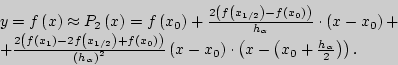
В данном случае график подынтегральной функции $y = f\left( x \right)$ на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ]$ заменяется дугой параболы с вертикальной осью, проходящей через точки $\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspac... ...eft/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right)} \right)$, $\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspac... ...phantom {{h_\alpha } 2}} \right. \kern-\nulldelimiterspace} 2} \right)} \right)$ и $\left( {x_1 ,f\left( {x_1 } \right)} \right) = \left( {x_0 + h_\alpha ,f\left( {x_0 + h_\alpha } \right)} \right)$.

Вычисление приближенного значения определенного интеграла на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ].$

$$\begin{array}{l} \int\limits_{x_0 }^{x_1 } {f\left( x \righ... ...right)} \right) \\ \end{array}} \right)dx} . \\ \end{array}$$

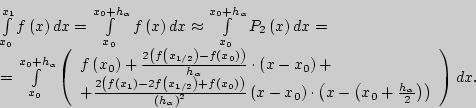
Выполним замену переменной:

$$t = \frac{x - x_0 }{h_\alpha }, \quad x = x_0 + t \cdot h_\alpha , \quad dx = h_\alpha dt.$$

$$x = x_0 \Rightarrow t = 0, \quad x = x_1 = x_0 + h_\alpha \Rightarrow t = 1.$$

Тогда

$$\begin{array}{l} \int\limits_{x_0 }^{x_0 + h_\alpha } {\lef... ...} } \right) + f\left( {x_1 } \right)} \right). \\ \end{array}$$

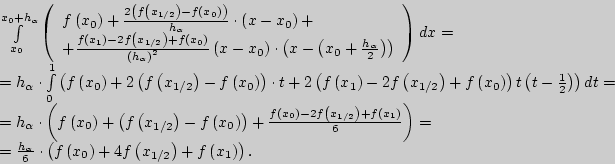
В итоге имеем:

$$\int\limits_{x_0 }^{x_1 } {f\left( x \right)dx} \approx \fra... ...elimiterspace} 2} } \right) + f\left( {x_1 } \right)} \right).$$

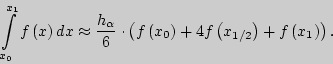
Таким образом, приближенное значение определенного интеграла на отрезке $[x_0 ,x_1 ] = [x_0 ,x_0 + h_\alpha ^{PT} ]$ равно площади параболической трапеции, ограниченной осью абсцисс, линиями, параллельными осям ординат и дугой параболы с вертикальной осью, проходящей через точки $\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspac... ...eft/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} } \right)} \right)$, $\left( {x_{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspac... ...phantom {{h_\alpha } 2}} \right. \kern-\nulldelimiterspace} 2} \right)} \right)$ и $\left( {x_1 ,f\left( {x_1 } \right)} \right) = \left( {x_0 + h_\alpha ,f\left( {x_0 + h_\alpha } \right)} \right)$.

Вычисление приближенного значения определенного интеграла по формуле параболических трапеций на отрезке $[a_0 ,b_0 ].$

$$\int\limits_{x_0 }^{x_1 } {f\left( x \right)dx} \approx \fra... ...elimiterspace} 2} } \right) + f\left( {x_1 } \right)} \right).$$

$$\begin{array}{l} \int\limits_{x_0 }^{x_2 } {f\left( x \righ... ...t)} \right) + f\left( {x_1 } \right)} \right). \\ \end{array}$$

$$\begin{array}{l} \int\limits_{x_0 }^{x_3 } {f\left( x \righ... ...1 } \right) + f\left( {x_2 } \right)} \right). \\ \end{array}$$
................................. ................................. ............

$$\int\limits_{x_0 }^{x_N } {f\left( x \right)dx} = \sum\limit... ...sum\limits_{J = 1}^{N - 1} {f\left( {x_J } \right)} } \right).$$

Тогда приближенное значение определенного интеграла на отрезке $[a_0 ,b_0 ]$ определяется согласно следующему соотношению:

$$\begin{array}{l} \int\limits_{a_0 }^{b_0 } {f\left( x \righ... ...1}^{S - 1} {f\left( {x_J } \right)} } \right). \\ \end{array}$$

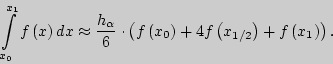
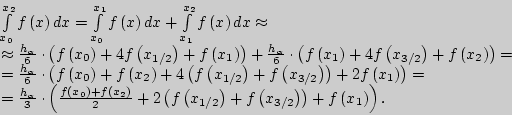
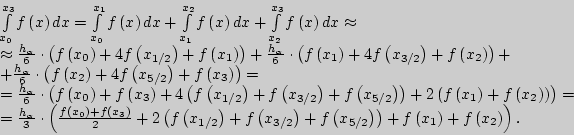
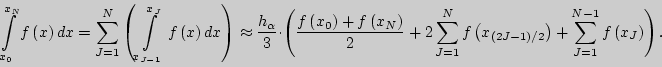
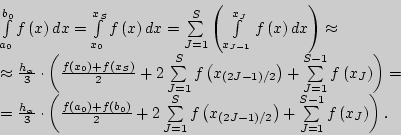
В данной лабораторной работе использование формулы параболических трапеций (Симпсона) ("FORMULA OF PARABOLIC TRAPEZOIDS") имеет следующую реализацию:

Итерация с индексом $''N'' \quad \left( {N \ge 1} \right)$:

На отрезке $\left[ {a_0 ,b_0 } \right]$ при соблюдении условия $a_0 < b_0$, исходя из вводимого или рассчитанного значения фиксированного шага $h_\alpha ^{PT}$ (при вводимом значении количества шагов $s_\alpha ^{PT}$ по формуле $h_\alpha ^{PT} = \frac{b_0 - a_0 }{s_\alpha ^{PT} })$, выбирается абсцисса точки подынтегральной функции с координатами $\left( {x_N^{PT} ,f\left( {x_N^{PT} } \right)} \right)$, то есть $x_N^{PT}$ согласно следующему соотношению: $x_N^{PT} = x_{N - 1}^{PT} + h_\alpha ^{PT}$.

Осуществляется расчет площади элементарной параболической трапеции $q_N^{PT}$, значение высоты которой $h_\alpha ^{PT} = x_N^{PT} - x_{N - 1}^{PT} = x_1^{PT} - x_0^{PT}$, согласно следующей формуле:

$$q_N^{PT} = \frac{h_\alpha ^{PT} }{6} \cdot \left( {f\left( {... ...ace} 2}^{PT} } \right) + f\left( {x_N^{PT} } \right)} \right).$$

Осуществляется расчет приближенного значения определенного интеграла на отрезке $\left[ {a_0 ,x_N^{PT} } \right]$ согласно следующему соотношению: $I_{\alpha N}^{PT} = I_{\alpha \left( {N - 1} \right)}^{PT} + q_N^{PT}$.

Если достигнута истинность выражения $x_N^{PT} \ge b_0$, то итерации прекращаются, количество шагов итераций $s_\alpha ^{PT} = N$, и приближенное значение определенного интеграла $I_\alpha ^{PT} = I_{\alpha N}^{PT}$.

Если $x_N^{PT} < b_0$, то осуществляется переход к следующей итерации.

Далее: Описание этапов проведения лабораторной Вверх: Лабораторная работа № 3 Назад: Лабораторная работа № 3