Далее: 1.2.  Задачи для самостоятельного Вверх: 1.  Молекулярная физика и Назад: 1.  Молекулярная физика и

1.1.  Примеры решения задач

Пример 1.1.  Сжиженные газы хранят в сосудах, сообщающихся с атмосферой. Можно ли допустить испарение жидкого азота объемом $0,5\,{л}$ и плотностью $0,81\,{г/см}^3$в закрытом сосуде объемом $10\,{л}$ при нагревании его до температуры $20^\circ C$, если стенки сосуда выдерживают давление $20\,{атм}$?

Решение. При повышении температуры жидкий азот перейдет в газообразное состояние. Примем его при температуре $20^\circ C$ за идеальный газ и применим для решения уравнение Клапейрона - Менделеева:

$$PV = {m\over\mu}RT\,,$$ (1)

где $P$, $V$ и $T$ - давление, объем и температура газа; $m$ - его масса, $\mu$ - масса моля азота, равная $28\cdot 10^{-3}\,{кг/моль}$; $R$ - универсальная газовая постоянная.

Для ответа на вопрос задачи нужно определить давление газообразного азота и сравнить его с максимально допустимым.

Выразим искомое давление из уравнения 1:

$$P_x = {mRT\over\mu V}\,,$$ (2)

здесь неизвестна масса газа, ее можно определить через объем и плотность жидкого азота: $m= \rho_1V_1$. Выражение для искомого давления в общем виде:

$$P_x = {\rho_1V_1RT\over\mu V}\,.$$ (3)

Проверка наименования единицы искомой величины:

$$[P_x]={{кг}\cdot{м}^3\cdot{Дж}\cdot{К}\cdot{моль}\over {м}^3 ... ...{{Дж}\over{м}^3}= {{Н}\cdot{м}\over{м}^3}={{Н}\over{м}^2}={Па.}$$

Это единица давления в СИ, следовательно, выражение в общем виде получено правильно.

Вычисления: подставим числа (все они должны быть выражены в СИ):

$$P_x={8,1\cdot 10^2\cdot 5\cdot 10^{-4}\cdot 8,3 \cdot 293\over 28\cdot 10^{-3}\cdot 10^{-2}}\,{Па}\,.$$

Прежде чем вычислять, проведем действия со степенями:

$$P_x={8,1\cdot 5\cdot 8,3 \cdot 293\over 28}\cdot 10^{3}\,{Па}=3,52\cdot 10^{6}\,{Па}\,.$$

Искомое давление равно $3,52\cdot 10^6\,{Па}$ или $35,2\ {атм}$ и превышает допустимое.

Ответ: испарение жидкого азота данной массы в закрытом сосуде указанного объема нельзя допустить, так как при $20^\circ C$ давление превысит допустимое. Поэтому сжиженные газы хранят в открытых сосудах.

Пример 1.2. Цилиндрическая трубка длиной $\ell$ наполовину погружена в ртуть. Закрыв ее сверху, трубку вынимают, при этом часть ртути выливается. Какой длины столбик ртути останется в трубке, если атмосферное давление равно $H$ мм рт. ст.?

Решение. Примем воздух, находящийся в трубке над ртутью, за идеальный газ. Поскольку в условии задачи изменение температуры не оговорено, к столбику воздуха можно применить закон Бойля - Мариотта:

$$P_1V_1 = P_2V_2\,,$$ (4)

где $P_1$ и $V_1$ -- давление и объем воздуха в первом состоянии; $P_2$ и $V_2$ -- то же во втором состоянии.

Для ответа на вопрос задачи нужно выразить параметры газа через известные в общем виде величины - $H$ и $\ell$. Обозначим искомую длину столбика ртути через $X$. В первом состоянии столбик воздуха длиной $\ell/2$, то есть объемом $V_1={S\ell\over 2}$ ($S$ - площадь сечения трубки), находился под атмосферным давлением, так как трубка была открыта сверху. Выразим атмосферное давление: $P_1 = \rho gH$, где $\rho$ - плотность ртути. Таким образом,

$$P_1V_1 = \rho gH{S\ell\over 2}\,.$$ (5)

Во втором состоянии длина столбика воздуха стала равной $(\ell-X)$, а его объем $V_2=S(\ell-X)$. Давление воздуха в сумме с давлением оставшегося столбика ртути высотой $X$ уравновешивается атмосферным давлением, действующим согласно закону Паскаля на нижний открытый конец трубки: $P_2+\rho gX=\rho gH$, откуда давление

$$P_2=\rho g(H-X)\ {и}$$

$$P_2V_2 = \rho g(H-X)S(\ell-X)\,.$$ (6)

Подставив выражения (5 и 6) в исходное уравнение (4) и сократив на $g,\ S,\ \rho$, получим квадратное уравнение относительно $X$:

$$X^2 - (H+\ell)X+{\ell H\over 2}=0\,.$$ (7)

Два корня этого уравнения:

$$X_{1,2} = {(H+\ell)\pm \sqrt{(H+\ell)^2-2\ell H}\over 2}={(H+\ell)\pm \sqrt{H^2+\ell^2}\over 2}\,.$$

Математическая часть задачи выполнена: найдены корни квадратного уравнения. Однако условию физической задачи корень уравнения со знаком "+" не удовлетворяет, так как длина столбика ртути в этом случае превышает длину трубки $\ell$. Поэтому
$X={(H+\ell)-\sqrt{H^2+\ell^2}\over 2}$. Видно, что $X$ получится в единицах длины. В числовом варианте решения подобной задачи $H$ и $\ell$ нужно подставлять в одинаковых единицах длины, например, в м.

Ответ: искомая длина столбика выражается так:

$$X={(H+\ell)-\sqrt{H^2+\ell^2}\over 2}\,.$$

Пример 1.3. В стеклянном сферическом сосуде с внутренним диаметром $3\,{см}$ находится азот, давление которого при температуре $-190^\circ C$ равно 1,33 Па. На стенках внутри сосуда имеется мономолекулярный (толщиной в одну молекулу) слой адсорбированного, то есть поглощенного поверхностным слоем, азота. Одна молекула занимает площадь $10^{-15}\,{см}^2$. Найти давление азота в сосуде при температуре $427^\circ C$, при которой он полностью десорбируется со стенок.

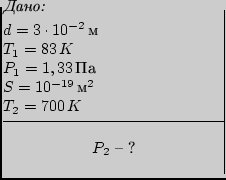Решение. Азот при таком низком давлении можно рассматривать как идеальный газ и применить соответствующую теорию. Искомое давление $P_2$ будет складываться из давления газа, первоначально находившегося в сосуде $P_2'$, и давления $P_2''$, которое создадут молекулы, перешедшие со стенок в cocуд при температуре $T_2$:

$$P_2 = P_2'+P_2''\,.$$ (8)

Выразим давление $P_2'$, учитывая, что повышение температуры происходит при постоянном объеме. Согласно закону Шарля:

$${P_1\over T_1}={P_2'\over T_2}\,,$$

$${откуда\quad\quad} P_2' = P_1{T_2\over T_1}\,.$$ (9)

Видно, что единица измерения $P_2'$ получается такая же, как $P_1$ - Па.

Давление $P_2''$ выразим из основного уравнения кинетической теории идеального газа:

$$P_2'' = nkT_2={N\over V}kT_2\,,$$ (10)

где $N$ - общее число десорбированных молекул, $n$ - их концентрация, $k$ - постоянная Больцмана, $V$ - объем сосуда: $V={\pi d^3\over 6}$. Общее число молекул, перешедших со стенок в сосуд, можно выразить как отношение площади внутренней поверхности сферического сосуда $\pi d^2$ к площади одной молекулы: $N={\pi d^2\over S}$. Окончательно для давления $P_2''$ получим:

$$P_2'' = {\pi d^2\cdot 6\cdot kT_2\over S\pi d^3}={6kT_2\over Sd}\,.$$ (11)

Проверка единиц измерения искомой величины:

$$[P_2'']={{Дж}\cdot{К}\over{К}\cdot{м}^2\cdot{м}}= {{Н}\cdot{м}\over{м}^3}={{Н}\over{м}^2}={Па}\,.$$

Получена единица давления, то есть выражение в общем виде правильно.

Таким образом,

$$P_2 = P_1 {T_2\over T_1}+{6kT_2\over Sd}\,.$$ (12)

Вычисления:

$$P_2=\left ({1,3\cdot 7\cdot 10^2\over 83}+{6\cdot 1,38\cdot 1... ...7\cdot 10^{2}\over 10^{-19}\cdot 3\cdot 10^{-2}}\right )\,{Па}=$$

$$=\left ( 11,22+{6\cdot 1,38 \cdot 7\over 3}\right)\,{Па}=(11,22+19,32)\,{Па}=30,54\,{Па}\,.$$

Видно, что по порядку величины действие обоих факторов: роста давления с повышением температуры и увеличения концентрации молекул в сосуде -- согласуется по порядку величин. Второй фактор в данном случае оказывает большее действие.

Ответ: давление азота в сосуде станет равным 30,54 Па.

Пример 1.4. Найти среднее число всех парных столкновений в секунду молекул кислорода, находящихся в объеме $1\,{см}^3$ при температуре $17^\circ C$ и давлении 666,5 Па.

Решение. Согласно МКТ идеального газа среднее число столкновений в секунду одной молекулы равно:

$$\overline{Z} = \sqrt{2}\pi d^2n\overline{v}\,,$$ (13)

где $d$ - эффективный диаметр молекулы, $n$ - концентрация газа, $\overline{v}$ - средняя арифметическая скорость молекул.

Если учитывать только парные
столкновения, число всех столкновений в секунду будет больше в ${N\over 2}={nV\over 2}$ раз, где $N$ - общее число молекул.

Тогда искомое число столкновений выразится так:

$$\overline{Z}={\sqrt{2}\pi d^2\overline{v}n^2V\over 2}\,.$$ (14)

Далее следует выразить концентрацию газа из основного уравнения кинетической теории идеального газа: $p=nkT$, а среднюю арифметическую скорость -- через параметры газа: $\overline{v}=\sqrt{8RT\over\pi\mu}$, где $R$ -- универсальная (молярная) газовая постоянная. После подстановки для искомой величины получается:

$$\overline{Z}=2\left({dP\over kT}\right)^2V\sqrt{\pi RT\over\mu}\,.$$ (15)

В этом выражении все, кроме диаметра молекулы, известно. Это число взято из таблицы.

Проверка единицы измерения искомой величины:

$$[\overline{Z}]={{м}^2\cdot{Н}^2\cdot{К}^2\cdot{м}^3\cdot{Дж}^... ... 2}\over{с}\cdot{м}^{3\over 2}\cdot{кг}^{1\over 2}}={с}^{-1}\,.$$

Наименование $c^{-1}$ соответствует числу столкновений в секунду.

Вычисления:

$$\overline{Z}={2\cdot 12,25\cdot 10^{-20}\cdot (666,5)^2\cdot ... ...\over327\cdot 10^{-3}}\,{с}^{-1} =3,3\cdot 10^{24}\,{с}^{-1}\,.$$

Ответ: при указанных условиях происходит $3,3\cdot 10^{24}$ парных столкновений молекул в секунду. Это число зависит от параметров состояния ($P,\ T$), объема газа и его индивидуальных характеристик: диаметра молекулы и молярной массы.

Пример 1.5. Расстояние между стенками сосуда равно $8\,{мм}$. При каком давлении вязкость газа, находящегося между ними, начнет уменьшаться при откачке? Температура газа равна $17^\circ C$. Диаметр молекулы составляет $3\cdot 10^{-10}\,{м}$.

Решение. Теоретически вязкость газа при не слишком низких давлениях  не зависит от него:

$$\eta = {1\over 3}\overline{v}\overline{\lambda}\rho\,,$$ (16)

так как $\overline{\lambda}$ - средняя длина свободного пробега молекул обратно пропорциональна давлению при постоянной температуре:

$$\overline{\lambda} = {1\over \sqrt{2}\pi d^2n}={kT\over \sqrt{2}\pi d^2P}\,,$$ (17)

а плотность газа $\rho$ прямо пропорциональна давлению. Выражение для плотности идеального газа можно получить из уравнения Клапейрона - Менделеева: $PV = {m\over\mu}RT$, учитывая, что плотность -- это масса единицы объема: $\rho = {m\over V}$. Получается, что $\rho = {\mu P\over RT}$.

При низком давлении средняя длина свободного пробега перестает зависеть от давления и определяется размерами сосуда:

$$\overline{\lambda} = \ell\,.$$ (18)

Молекулы движутся от стенки к стенке, не сталкиваясь между собой. Вязкость газа начнет уменьшаться при дальнейшей откачке сосуда за счет уменьшения концентрации молекул (плотности газа).

Для решения задачи нужно приравнять выражение для средней длины свободного пробeгa молекул $\overline{\lambda}$ расстоянию между стенками сосуда:

$$\ell = {kT\over \sqrt{2}\pi d^2P}\,$$

и выразить давление. Получаем:

$$P = {kT\over \sqrt{2}\pi d^2\ell}\,.$$ (19)

В этом выражении для давления все известно.

Проверка наименования единицы измерения:

$$[P]={{Дж}\cdot{К}\over{К}\cdot{м}^2\cdot{м}}={{Дж}\over {м}^3}={{Н}\cdot{м}\over{м}^3}={{Н}\over{м}^2}={Па}\,.$$

Выражение для давления в общем виде получено правильно.

Вычисления:

$$P={1,38\cdot 10^{-23}\cdot 290\over \sqrt{2}\cdot 3,14\cdot 9... ...290\over \sqrt{2}\cdot 3,14\cdot 9\cdot 8}\,{Па}=1,26\, {Па}\,.$$

Полученное число значительно меньше величины атмосферного давления. Для данного газа при неизменной температуре оно определяется только размерами сосуда $\ell$.

Ответ: при давлении 1,26 Па вязкость газа начнет уменьшаться при откачке. Указание: подобным образом решаются задачи, связанные с коэффициентом теплопроводности идеального газа:

$$\chi = {1\over 3}\overline{v}\overline{\lambda}\rho c_v\,,$$

где $c_v$ - удельная теплоемкость при постоянном объеме:

$$c_v={i\over 2}{R\over\mu}\ (i{ -- число степеней свободы молекулы}).$$

Пример 1.6. 10 л азота, находящегося под давлением $10^5\,{Па}$, расширяются вдвое. Найти конечное давление и совершенную газом работу в случаях изобарического, изотермического и адиабатического процессов. Молекулы азота имеют пять степеней свободы.

Решение. Примем азот в данных условиях за идеальный газ. 1. При изобарическом процессе давление газа не меняется, поэтому $P_2=P_1$. Элементарная работа расширения равна в общем случае $PdV$, где $P$ - давление, $dV$ - бесконечно малый объем. Полная работа находится путем интегрирования, и величина eе зависит от вида процесса.

При изобарическом процессе

$$A_1=\int\limits_{V_1}^{V_2}{PdV}=P(V_2-V_1)\,.$$ (20)

Проверим единицу измерения работы:

$$[A]= {{Н}\cdot {м}^3\over {м}^2}={Н}\cdot{м}={Дж}\,.$$

2. В изотермическом процессе температура остается постоянной, а давления и объемы в двух состояниях идеального газа связаны законом Бойля - Мариотта: $P_1V_1=P_2V_2$, откуда $P_2'={P_1V_1\over V_2}$. Видно, что здесь для единицы неизвестного давления получается Па (паскаль).

Работа изотермического расширения рассчитывается так:

$$A_2=\int{PdV}=\int\limits_{V_1}^{V_2}{{m \over \mu}RT{dV\over V}}={m\over\mu}RT\ln{V_2 \over V_1}\,.$$

Здесь давление выражено из уравнения Клапейрона - Менделеева. Температура неизвестна, поэтому, применив еще раз уравнение Клапейрона - Менделеева, получим выражение для искомой работы через известные в условии величины:

$$A_2 = P_1V_1\ln{V_2\over V_1}\,.$$ (21)

Результат не изменится, если подставить конечные давление и объем $P_2$ и $V_2$ или вместо отношения ${V_2\over V_1}$ взять ${P_1\over P_2}$.

3. Конечное давление адиабатического расширения выразим из уравнения Пуассона:

$$P_2''=P_1\left({V_1\over V_2}\right)^\gamma\,,\ {где }\gamma={C_p\over C_V}={i+2\over i}$$

($i$ - число степеней свободы молекулы).

Работа в этом процессе совершается за счет убыли внутренней энергии газа:

$$A_3=-\Delta u={m\over\mu}C_V(T_1-T_2)={m\over\mu}C_V T_1 \left(1-{T_2\over T_1}\right)\,,$$

где $C_V$ - молярная теплоемкость при постоянном объеме:

$$C_V={i\over 2}R={R\over \gamma-1}\,.$$

В этой задаче температуры не заданы, поэтому отношение температур следует заменить отношением объемов ${T_2\over T_1}=\left({V_1\over V_2}\right)^{\gamma-1}$ и воспользоваться уравнением состояния идеального газа:

$$A_3={m\over\mu}{R\over(\gamma-1)}T_1\left(1-{T_2\over T_1}\ri... ...amma-1)} \left(1-\left({V_1\over V_2}\right)^{\gamma-1}\right)=$$

$$={1\over\gamma-1}(P_1V_1-P_2''V_2)\,.$$ (22)

Здесь все известно, конечное давление можно рассчитать отдельно.

Вычисления:

1. $P_2=P_1=10^{5}\,{Па}\,;\quad A_1=10^{5}\cdot 10^{-2}\,{Дж}=10^{3}\,{Дж}$.
2. $P_2'={10^{5}\cdot 10^{-2}\over 2\cdot 10^{-2}}\,{Па}=5\cdot 10^{4}\,{Па}\,;$

   $A_2=10^{5}\cdot 10^{-2}\ln{2\cdot 10^{-2}\over 10^{-2}}\,{Дж}=10^{3}\ln{2}\,{Дж}= 6,9\cdot 10^2\,{Дж}.$

3. $P_2''= 10^{5}\cdot 0,5^{1,4}\,{Па}=3,8\cdot 10^4\,{Па}\,;$

   $A_3={1\over 0,4}(10^3-760)\,{Дж}=600\,{Дж}\,.$

Таким образом, наибольшее изменение давления происходит при адиабатическом расширении, а наибольшая работа совершается при изобарическом. Качественно результаты представлены на рисунке. Площади фигур под графиками процессов позволяют судить о соотношении совершенной работы.

Ответ: $10^{5}\,{Па}\,,\ 10^{3}\,{Дж}\,;\ 5\cdot 10^{4}\,{Па}\,,\ 690\,{Дж}\,;\ 3,8\cdot 10^4\,{Па}\,,\ 600\,{Дж}.$

Пример 1.7. Холодильная машина, работающая по обратному циклу Карно, передает теплоту от холодильника с водой при температуре $0^\circ C$ кипятильнику с водой при температуре $100^\circ$C. Какую массу воды нужно заморозить в холодильнике, чтобы превратить в пар 1 кг воды в кипятильнике? Удельная теплота парообразования воды при $100^\circ$С равна $2,26\cdot 10^6\,{Дж/кг}$. Удельная теплота плавления льда равна $3,35\cdot 10^5\,{Дж/кг}$.

Решение. Холодильная машина за счет внешней работы отнимает некоторое количество теплоты $Q_2$ от менее нагретого тела при температуре $T_2$ и передает теплоту $Q_1$ более нагретомy телу при температуре $T_1$. Коэффициент полезного действия ее $\eta={A\over Q_1}={Q_1-Q_2\over Q_1}$.

Такое же соотношение справедливо и для тепловой машины, совершающей работу за счет части теплоты, взятой у более нагретого тела.

Наибольший коэффициент полезного действия соответствует идеальному (теоретическому) циклу Карно. В этом случае $\eta={Q_1-Q_2\over Q_1}={T_1-T_2\over T_1}$, то есть кпд определяется только температурами нагревателя (тела при температуре $T_1$) и холодильника ($T_2$). С помощью этого соотношения решается большинство задач, связанных с работой тепловых и холодильных машин. В реальных машинах кпд значительно меньше, чем ${T_1-T_2\over T_1}$.

В данной задаче количество теплоты $Q_1$, передаваемое более нагретому телу, равно $rm_1$, а количество теплоты $Q_2$, взятое от менее нагретого тела, равно $\lambda m_2$, поэтому справедливо равенство:

$${rm_1-\lambda m_2\over rm_1}={T_1-T_2\over T_1}\,,$$ (23)

которое можно преобразовать так:

$${\lambda m_2\over rm_1}={T_2\over T_1}\,,$$

$${откуда}\quad m_2={rm_1T_2\over\lambda T_1}\,.$$ (24)

Проверка наименования единицы:

$$[m]= {{Дж}\cdot {кг}\cdot {К}\cdot {кг}\over{кг}\cdot{Дж}\cdot {К}}={кг}\,.$$

Вычисления:

$$m_2={2,26\cdot 10^{6}\cdot 1\cdot 273\over 3,35\cdot 10^{5}\c... ...73}\,{кг}={2,26\cdot 2730\over 3,35\cdot 373}\,{кг}=4,94\,{кг}.$$

Ответ: чтобы испарить 1 кг воды в кипятильнике при заданных условиях, нужно заморозить 4,94 кг воды в холодильнике.

Далее: 1.2.  Задачи для самостоятельного Вверх: 1.  Молекулярная физика и Назад: 1.  Молекулярная физика и