Для более полного описания результатов эмпирического исследования используются меры разброса данных, характеризующие степень индивидуальных отклонений от центральной тенденции. Это самый простой показатель, который можно получить для выборки - разность между максимальной и минимальной величинами данного конкретного вариационного ряда. Мера разброса данных позволяет сравнивать между собой разные группы. Чем сильней варьирует измеряемый признак, тем больше величина разброса данных и наоборот.
Необходимо отметить, что данная мера крайне неточна и неустойчива. Единственный необычно высокий или низкий результат может повлиять на величину размаха.
Более точный метод измерения разброса данных основан на учете разности между каждым
индивидуальным результатом и среднеарифметическим значением по группе. Такой
мерой разброса является дисперсия или средний квадрат отклонения (![]() .
.
Дисперсия характеризует насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонение или разброс данных. Дисперсия определяется по следующей формуле:
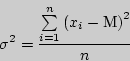
где ![]() - дисперсия
- дисперсия
![]() - выражение, означающее, что для всех значений x от первого до последнего в данной выборке вычисляется
разность между частными и средними значениями, эти разности возводятся в квадрат и суммируются
- выражение, означающее, что для всех значений x от первого до последнего в данной выборке вычисляется
разность между частными и средними значениями, эти разности возводятся в квадрат и суммируются
n - объем выборки
Вычислим дисперсию (![]() для следующего ряда: 2, 4, 6, 8, 10. Прежде
всего, найдем среднее (М) для данного ряда, оно равно 6.
для следующего ряда: 2, 4, 6, 8, 10. Прежде
всего, найдем среднее (М) для данного ряда, оно равно 6.
Из каждого элемента ряда вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Экспериментальные данные этой задаче, необходимые для расчета дисперсии, представим в виде (табл. 5)
| Первичный результат
|
|
|
| 2 | - 4 | 16 |
| 4 | - 2 | 4 |
| 6 | 0 | 0 |
| 8 | 2 | 4 |
| 10 | 4 | 16 |
| М = 6 |
|
Далее разности возводят в квадрат суммируются. Полученную сумму квадратов
разностей делим на объем данной выборки. В нашем примере получится
следующее:
![]()
Общий алгоритм вычисления дисперсии (![]() следующий:
следующий:
Вычисляется среднее по выборке
Для каждого элемента выборки вычисляется его отклонение от среднего.
Каждый элемент множества возводят в квадрат.
Находится сумма этих квадратов.
Эта сумма делится на общее количество членов используемой выборки.
Очень часто вместо дисперсии для выявления разброса частных данных
относительно средней используют производную от дисперсии величину,
называемую стандартным отклонением. Стандартное отклонение равно квадратному корню, извлекаемому из
дисперсии (![]() , и обозначается тем же знаком, только без квадрата
(
, и обозначается тем же знаком, только без квадрата
(![]() . Эта величина в ряде случаев оказывается более удобной
характеристикой варьирования, чем, дисперсия, так как выражается в тех же
единицах, что и средняя арифметическая величина.
. Эта величина в ряде случаев оказывается более удобной
характеристикой варьирования, чем, дисперсия, так как выражается в тех же
единицах, что и средняя арифметическая величина.
В нашем примере
![]()
О чем же свидетельствует стандартное отклонение равное 2, 58? Оно позволяет сказать, что большая часть результатов данного исследования располагается в пределах 2, 58 от средней, т. е. между 3, 42 (6 - 2,58) и 8, 58 (6 + 2,58).
Для того чтобы лучше понять, что подразумевается под ``большей частью
результатов'', необходимо рассмотреть те свойства стандартного отклонения,
которые проявляются при нормальной или приблизительно нормальной кривой
распределения, так как здесь существует прямое соответствие между ![]() и
относительным количеством случаев. На рис. 3 по горизонтальной оси отложены
интервалы, соответствующие отклонению в 1
и
относительным количеством случаев. На рис. 3 по горизонтальной оси отложены
интервалы, соответствующие отклонению в 1![]() , 2
, 2![]() и 3
и 3![]() вправо и влево от среднего значения (М). Процент случаев, приходящийся на
интервал М + 1
вправо и влево от среднего значения (М). Процент случаев, приходящийся на
интервал М + 1![]() в нормальном распределении, равен 34, 13. Поскольку
кривая симметрична, 34,13 случаев приходится также на интервалы от М -
1
в нормальном распределении, равен 34, 13. Поскольку
кривая симметрична, 34,13 случаев приходится также на интервалы от М -
1![]() , так, что диапазон от - 1
, так, что диапазон от - 1![]() до + 1
до + 1![]() охватывает 68,
26 % случаев. Почти все случаи (99,72%), т. е. почти все показатели
лежат в пределе от - 3
охватывает 68,
26 % случаев. Почти все случаи (99,72%), т. е. почти все показатели
лежат в пределе от - 3![]() до + 3
до + 3![]() относительно среднего
значения.
относительно среднего
значения.
![\includegraphics[width=4.81in,height=2.83in]{D:/html/work/link1/metod/met125/met1253.eps}](img24.png)
Эта закономерность известна как закон ``трех сигм'' и является одной из характеристик нормального распределения.