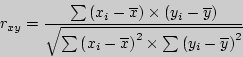
Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона.
В общем виде формула для подсчета коэффициента корреляции такова:
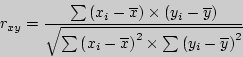
где ![]() - значения, принимаемые переменной X,
- значения, принимаемые переменной X,
![]() - значения, принимаемые переменой Y,
- значения, принимаемые переменой Y,
![]() - средняя по X,
- средняя по X,
![]() - средняя по Y.
- средняя по Y.
Расчет коэффициента корреляции Пирсона предполагает, что переменные ![]() и
и ![]() распределены нормально.
распределены нормально.
Даная формула предполагает, что из каждого значения ![]() переменной X,
должно вычитаться ее среднее значение
переменной X,
должно вычитаться ее среднее значение ![]() . Это не удобно, поэтому
для расчета коэффициента корреляции используют не данную формулу, а ее
аналог, получаемый с помощью преобразований:
. Это не удобно, поэтому
для расчета коэффициента корреляции используют не данную формулу, а ее
аналог, получаемый с помощью преобразований:
![\begin{displaymath}
rx = \frac{n\times \sum {\left( {x_i \times y_i } \right) - ...
...mes \sum {y_i^2
- \left( {\sum {y_i} } \right)^2} } \right]} }
\end{displaymath}](img102.png)
Используя данную формулу, решим следующую задачу:
Пример: 20 школьникам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X - обозначает среднее время решения наглядно-образных, а переменная Y - среднее время решения вербальных заданий тестов.
Для решения данной задачи представим исходные данные в виде табл. 12, в которой введены дополнительные столбцы, необходимые для расчета по формуле
В табл. 12 даны индивидуальные значения переменных X и Y, построчные произведения переменных X и Y, квадраты переменных всех индивидуальных значений переменных X и Y, а также суммы всех вышеперечисленных величин.
| № испытуемых | X | Y | X |
X |
Y |
| Среднее время решения наглядно-образных заданий | Среднее время решения вербальных заданий | ||||
| 1 | 19 | 17 | 323 | 361 | 289 |
| 2 | 32 | 7 | 224 | 1024 | 49 |
| 3 | 33 | 17 | 561 | 1089 | 289 |
| 4 | 44 | 28 | 1232 | 1936 | 784 |
| 5 | 28 | 27 | 756 | 784 | 729 |
| 6 | 35 | 31 | 1085 | 1225 | 961 |
| 7 | 39 | 20 | 780 | 1521 | 400 |
| 8 | 39 | 17 | 663 | 1521 | 289 |
| 9 | 44 | 35 | 1540 | 1936 | 1225 |
| 10 | 44 | 43 | 1892 | 1936 | 1849 |
| 11 | 24 | 10 | 240 | 576 | 100 |
| 12 | 37 | 28 | 1036 | 1369 | 784 |
| 13 | 29 | 13 | 377 | 841 | 169 |
| 14 | 40 | 43 | 1720 | 1600 | 1849 |
| 15 | 42 | 45 | 1890 | 1764 | 2025 |
| 16 | 32 | 24 | 768 | 1024 | 5760 |
| 17 | 48 | 45 | 2160 | 2304 | 2025 |
| 18 | 42 | 26 | 1092 | 1764 | 676 |
| 19 | 33 | 16 | 528 | 1089 | 256 |
| 20 | 47 | 26 | 1222 | 2209 | 676 |
| Сумма | 731 | 518 | 20089 | 27873 | 16000 |
Рассчитываем эмпирическую величину коэффициента корреляции по формуле:
Определяем критические значения для полученного коэффициента корреляции по табл. 19 приложения 6.
Отметим, что в табл. 19 приложения 6 величины критических значений коэффициентов линейной корреляции Пирсона даны по абсолютной величине. Следовательно, при получении как положительного, так и отрицательного коэффициента корреляции по формуле оценка уровня значимости этого коэффициента проводится по той же таблице приложения без учета знака, а знак добавляется для дальнейшей интерпретации характера связи между переменными X и Y.
При нахождении критических значений для вычисленного коэффициента корреляции Пирсона
![]() число степеней свободы рассчитывается как
число степеней свободы рассчитывается как ![]() .
.
В нашем случае k = 20,
поэтому n - 2 = 20 - 2 = 18. В первом столбце табл. 19 приложения 6 в
строке, обозначенной числом 18, находим ![]() :
:
0,44 для P ![]() 0,05
0,05
0,56 для P ![]() 0,01
0,01
Строим соответствующую ``ось значимости'':
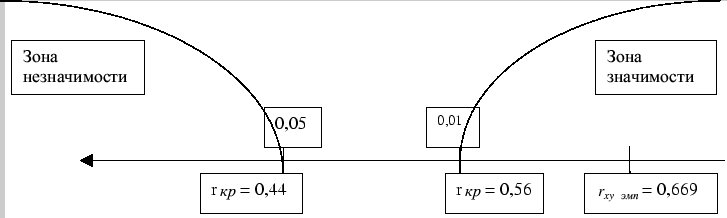
Ввиду того, что величина расчетного коэффициента корреляции попала в зону
значимости - ![]() отвергается и принимается гипотеза
отвергается и принимается гипотеза ![]() .
Иными словами, связь между временем решения наглядно-образных и вербальных
задач статистически значима на 1% уровне и положительна. Полученная прямо
пропорциональная зависимость говорит о том, что чем выше среднее время
решения наглядно-образных задач, тем выше среднее время решения вербальных и
наоборот.
.
Иными словами, связь между временем решения наглядно-образных и вербальных
задач статистически значима на 1% уровне и положительна. Полученная прямо
пропорциональная зависимость говорит о том, что чем выше среднее время
решения наглядно-образных задач, тем выше среднее время решения вербальных и
наоборот.
Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:
Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.
Распределения переменных X и Y должны быть близки к нормальному.
Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
Таблицы уровней значимости для коэффициента корреляции Пирсона (таблица 19 приложения 6) рассчитаны от n = 5 до n = 1000. Оценка уровня значимости по таблицам осуществляется при числе степеней свободы k = n - 2.