Далее: Приложения Вверх: 8.6. Корреляционный анализ Назад: 8.6.1. Коэффициент корреляции Пирсона

8.6.2. Коэффициент корреляции рангов Спирмена

Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин.

Величина коэффициента корреляции Спирмена также лежит в интервале +1 и -1. Он, как и коэффициент Пирсона, может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале.

В принципе число ранжируемых признаков (качеств, черт и т.п.) может быть любым, но сам процесс ранжирования большего, чем 20 числа признаков -- затруднителен. Возможно, что именно поэтому таблица критических значений рангового коэффициента корреляции рассчитана лишь для сорока ранжируемых признаков (n < 40, табл. 20 приложения 6).

Ранговый коэффициент корреляции Спирмена подсчитывается по формуле:

$$P = 1 - \frac{6\times \sum {\left( {D^2} \right)} }{n\times \left( {n^2 - 1} \right)}$$

где n - количество ранжируемых признаков (показателей, испытуемых);

D - разность между рангами по двум переменным для каждого испытуемого;

$\sum {\left( {D^2} \right)}$ - сумма квадратов разностей рангов.

Используя ранговый коэффициент корреляции, рассмотрим следующий пример.

Пример: Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у 11 первоклассников и их средняя успеваемость в конце учебного года.

Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлении в школу, и, во-вторых, итоговые показатели успеваемости в конце года у этих же учащихся в среднем. Результаты представим в табл. 13.

Таблица 13

№ учащихся	1	2	3	4	5	6	7	8	9	10	11
Ранги показателей школьной готовности	3	5	6	1	4	11	9	2	8	7	10
Ранги среднегодовой успеваемости	2	7	8	3	4	6	11	1	10	5	9
$D$	1	-2	-2	-2	0	5	-2	1	-2	2	1
$D^2$	1	4	4	4	0	25	4	1	4	4	1

Подставляем полученные данные в формулу и производим расчет. Получаем:

$$P_{{эмп}} = 1 - \frac{6\times 52}{11\times \left( {11\times 11 - 1} \right)} = 0,76$$

Для нахождения уровня значимости обращаемся к табл. 20 приложения 6, в которой приведены критические значения для коэффициентов ранговой корреляции.

Подчеркнем, что в табл. 20 приложения 6, как и в таблице для линейной корреляции Пирсона, все величины коэффициентов корреляции даны по абсолютной величине. Поэтому, знак коэффициента корреляции учитывается только при его интерпретации.

Нахождение уровней значимости в данной таблице осуществляется по числу n, т. е. по числу испытуемых. В нашем случае n = 11. Для этого числа находим $r_{кр}$:

0,61 для P $\le$ 0,05

0,76 для P $\le$ 0,01

Строим соответствующую ``ось значимости'':

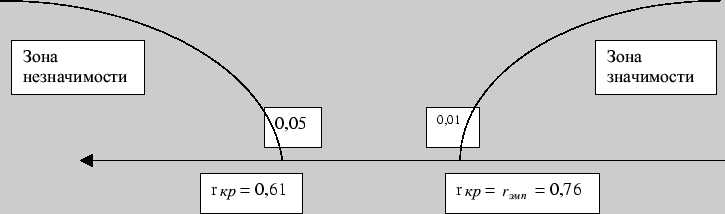
Полученный коэффициент корреляции совпал с критическим значением для уровня значимости в 1%. Следовательно, можно утверждать, что показатели школьной готовности и итоговые оценки первоклассников связаны положительной корреляционной зависимостью - иначе говоря, чем выше показатель школьной готовности, тем лучше учится первоклассник. В терминах статистических гипотез психолог должен отклонить нулевую (Н$_{{о}})$ гипотезу о сходстве и принять альтернативную (Н$_{1})$ о наличии различий, которая говорит о том, что связь между показателями школьной готовности и средней успеваемостью отлична от нуля.

Случай одинаковых (равных) рангов

При наличии одинаковых рангов формула расчета коэффициента линейной корреляции Спирмена будет несколько иной. В этом случае в формулу вычисления коэффициентов корреляции добавляются два новых члена, учитывающие одинаковые ранги. Они называются поправками на одинаковые ранги и добавляются в числитель расчетной формулы.

$$D1 = \frac{n^3 - n}{12}$$

$$D2 = \frac{k^3 - k}{12}$$

где n - число одинаковых рангов в первом столбце,

k - число одинаковых рангов во втором столбце.

Если имеется две группы одинаковых рангов, в каком-либо столбце то формула поправки несколько усложняется:

$$D3 = \frac{\left( {n^3 - n} \right) + \left( {k^3 - k} \right)}{12}$$

где n - число одинаковых рангов в первой группе ранжируемого столбца,

k - число одинаковых рангов в второй группе ранжируемого столбца. Модификация формулы в общем случае такова:

$$P_{{эмп}} = 1 - \frac{6\times \sum {d{ }^2} + D1 + D2 + D3}{n\times \left( {n^2 - 1} \right)}$$

Пример: Психолог, используя тест умственного развития (ШТУР) проводит исследование интеллекта у 12 учащихся 9 класса. Одновременно с этим, но просит учителей литературы и математики провести ранжирование этих же учащихся по показателям умственного развития. Задача заключается в том, чтобы определить, как связаны между собой объективные показатели умственного развития (данные ШТУРа) и экспертные оценки учителей.

Экспериментальные данные этой задачи и дополнительные столбцы, необходимые для расчета коэффициента корреляции Спирмена, представим в виде табл. 14.

Таблица 14

№ учащихся	Ранги тестирования с помощью ШТУРа	Экспертные оценки учителей по математики	Экспертные оценки учителей по литературе	D (второго и третьего столбцов)	D (второго и четвертого столбцов)	$D^2$(второго и третьего столбцов)	$D^2$(второго и четвертого столбцов)
1	6	5	5	1	1	1	1
2	7	10	8	-3	-1	9	1
3	4	8	7	-4	-3	16	9
4	5	4	11	1	-6	1	36
5	9	6	3	3	6	9	36
6	12	8	6	4	6	16	36
7	2,5	2	11	0,5	-8,5	0,25	77,25
8	2,5	3	11	-0,5	-8,5	0,25	77,25
9	10	8	1	2	9	4	81
10	8	11	3	-3	5	9	25
11	11	12	3	-1	8	1	64
12	1	1	9	0	-8	0	64
Суммы	78	78	78	0	0	66,5	471,5

Поскольку при ранжировании использовались одинаковые ранги, то необходимо проверить правильность ранжирования во втором, третьем и четвертом столбцах таблицы. Суммирование в каждом из этих столбцов дает одинаковую сумму - 78.

Проверяем по расчетной формуле. Проверка дает:

$$\frac{N\times \left( {N + 1} \right)}{2} = 12\times 13,2 = 78$$

В пятом и шестом столбцах таблицы приведены величины разности рангов между экспертными оценками психолога по тесту ШТУР для каждого ученика и величинами экспертных оценок учителей, соответственно по математике и литературе. Сумма величин разностей рангов должна быть равна нулю. Суммирование величин D в пятом и шестом столбцах дало искомый результат. Следовательно, вычитание рангов проведено правильно. Подобную проверку необходимо делать каждый раз при проведении сложных видов ранжирования.

Прежде, чем начать расчет по формуле необходимо рассчитать поправки на одинаковые ранги для второго, третьего и четвертого столбцов таблицы.

В нашем случае во втором столбце таблицы два одинаковых ранга, следовательно, по формуле величина поправки D1 будет: $D1 = \frac{2\times 2\times 2 - 2}{12} = 0,5$

В третьем столбце три одинаковых ранга, следовательно, по формуле величина поправки D2 будет: $D2 = \frac{3\times 3\times 3 - 3}{12} = 2$

В четвертом столбце таблицы две группы по три одинаковых ранга, следовательно, по формуле величина поправки D3 будет: $D3 = \frac{\left( {3\times 3\times 3 - 3} \right) + \left( {3\times 3\times 3 - 3} \right)}{12} = 4$

Прежде, чем преступить к решению задачи, напомним, что психолог выясняет два вопроса - как связаны величины рангов по тесту ШТУР с экспертными оценками по математике и литературе. Именно поэтому расчет проводится дважды.

Считаем первый ранговый коэффициент $P_{{эмп}}$ с учетом добавок по формуле. Получаем:

$$P_{{эмп}} = 1 - \frac{6\times 66,5 + 0,5 + 2}{12\times 143} = 1 - 0,233 = 0,767$$

Подсчитаем без учета добавки:

$$P_{{эмп}} = 1 - \frac{6\times 66,5}{12\times 143} = 1 - 0,232 = 0,768$$

Как видим, разница в величинах коэффициентов корреляции оказалась очень незначительной.

Считаем второй ранговый коэффициент $P_{{эмп}}$ с учетом добавок по формуле. Получаем:

$$P_{{эмп}} = 1 - \frac{6\times 471,5 + 0,5 + 4}{12\times 143} = 1 - 1,651 = - 0,651$$

Подсчитаем без учета добавки:

$$P_{{эмп}} = 1 - \frac{6\times 471,5}{12\times 143} = 1 - 1,648 = - 0,648$$

И опять, различия оказались очень незначительны. Поскольку число учащихся в обоих случаях одинаково, по табл. 20 приложения 6 находим критические значения при n = 12 сразу для обоих коэффициентов корреляции.

0,58 для P $\le$ 0,05

0,73 для P $\le$ 0,01

Откладываем первое значение $P_{{эмп}}$ на ``оси значимости'':

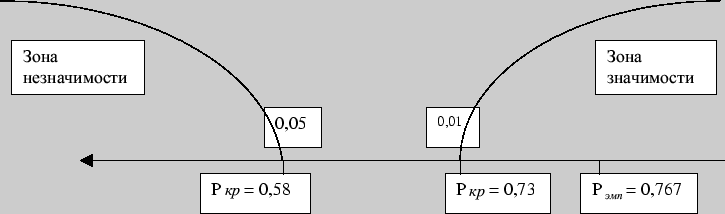
В первом случае полученный коэффициент ранговой корреляции находится в зоне значимости. Поэтому психолог должен отклонить нулевую Н$_{{о}}$ гипотезу о сходстве коэффициента корреляции с нулем и принять альтернативную Н$_{1}$ о значимом отличии коэффициента корреляции от нуля. Иными словами, полученный результат говорит о том, что чем выше экспертные оценки учащихся по тесту ШТУР, тем выше их экспертные оценки по математике.

Откладываем второе значение $P_{{эмп}}$ на ``оси значимости'':

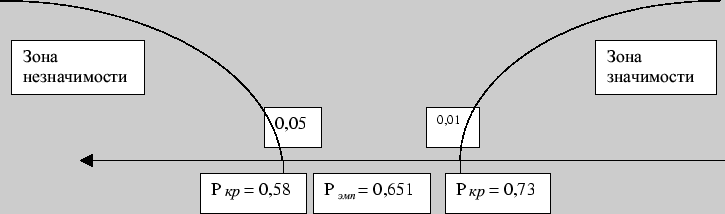
Во втором случае коэффициент ранговой корреляции находится в зоне неопределенности. Поэтому психолог может принять нулевую Н$_{{о}}$ гипотезу о сходстве коэффициента корреляции с нулем и отклонить альтернативную Н$_{1}$о значимом отличии коэффициента корреляции от нуля. В этом случае полученный результат говорит о том, что экспертные оценки учащихся по тесту ШТУР не связаны с экспертными оценками по литературе.

Для применения коэффициента корреляции Спирмена, необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть получены в порядковой (ранговой) шкале, но могут быть измерены также в шкале интервалов и отношений.

2. Характер распределения коррелируемых величин не имеет значения.

3. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.

Таблицы для определения критических значений коэффициента корреляции Спирмена (табл. 20 приложение 6) рассчитаны от числа признаков равных n = 5 до n = 40 и при большем числе сравниваемых переменных следует использовать таблицу для пирсоновского коэффициента корреляции (табл. 19 приложение 6). Нахождение критических значений осуществляется при k = n.

Далее: Приложения Вверх: 8.6. Корреляционный анализ Назад: 8.6.1. Коэффициент корреляции Пирсона