Вопросы теории
Кривые на плоскости. Способы задания кривых: явной функциональной
зависимостью, неявной функциональной зависимостью,
векторно-параметрическим представлением,
координатно-параметрическим представлением. Регулярное задание
кривой и его кинематическая интерпретация. Асимптотическое
поведение кривой. Формула длины кривой и ее кинематическая
интерпретация. Кривизна кривой на плоскости и ее кинематическая
интерпретация.
Основные определения, результаты, комментарии
Элементарной кривой на плоскости называется образ открытого
интервала
![]() при его гомеоморфизме
при его гомеоморфизме
![]() в евклидову плоскость (рис. 10).
в евклидову плоскость (рис. 10).
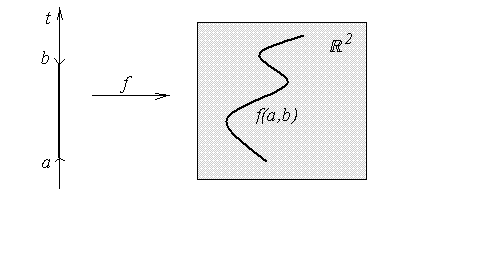
Общей кривой на плоскости называется подмножество евклидовой плоскости, локально гомеоморфное прямой (рис. 11).

Очевидно, всякая общая кривая допускает покрытие элементарными кривыми.
Говорят, что кривая ![]() задана явной функциональной
зависимостью
задана явной функциональной
зависимостью ![]() , если каждая точка кривой
, если каждая точка кривой
![]() принадлежит графику функции
принадлежит графику функции ![]() .
.
Кривая ![]() задана неявной функциональной зависимостью
задана неявной функциональной зависимостью
![]() если координаты каждой точки кривой
если координаты каждой точки кривой ![]() удовлетворяют уравнению
удовлетворяют уравнению ![]()
Для вычислений в дифференциальной геометрии наиболее удобны векторно-параметрическое представление
Параметрическое представление кривой называется регулярным,
если индуцированное им отображение
![]() является локальным гомеоморфизмом на свой образ. Для этого
необходимо и достаточно, чтобы
является локальным гомеоморфизмом на свой образ. Для этого
необходимо и достаточно, чтобы
![]() для всех
для всех
![]() Назовем параметризацию
Назовем параметризацию ![]() -регулярной, если
вектор-функция
-регулярной, если
вектор-функция
![]() обладает непрерывной производной
порядка
обладает непрерывной производной
порядка ![]() .
.
Говорят, что заданная параметрическим способом кривая
![]() уходит в бесконечность при
уходит в бесконечность при ![]() если имеет место
предельное соотношение
если имеет место
предельное соотношение
При этом символ ![]() может иметь одно из следующих значений:
может иметь одно из следующих значений:
Асимптотой кривой
![]() при
при ![]() называется прямая
называется прямая ![]() , удовлетворяющая условию:
, удовлетворяющая условию:
Для вычисления уравнений асимптот пользуются следующим правилом.
Если кривая, заданная параметрическим способом, уходит в
бесконечность при ![]() , то асимптота, если она существует,
задается уравнением
, то асимптота, если она существует,
задается уравнением ![]() (соответственно,
(соответственно, ![]() ), где
), где

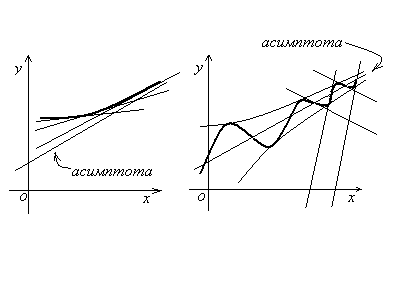
На первый взгляд, можно было бы определить асимптоту как предельное положение касательной в точке данной кривой при удалении этой точки на бесконечность. В ряде случаев это определение приводит к тем же результатам, что и классическое. Вместе с тем можно построить кривые, имеющие касательную в каждой своей точке и имеющие асимптоту в данном направлении, но не имеющие предельного положения касательной в данном направлении (рис. 12).
В случае задания кривой неявным алгебраическим
уравнением
![]() также существует способ отыскания
асимптот, заключающийся в следующем. Пусть
также существует способ отыскания
асимптот, заключающийся в следующем. Пусть
![]() -
координаты точки, принадлежащей асимптоте, и
-
координаты точки, принадлежащей асимптоте, и
![]()
![]() - параметрические уравнения асимптоты, в
которых
- параметрические уравнения асимптоты, в
которых ![]() - параметр,
- параметр,
![]() - координаты
направляющего вектора, подлежащие определению.
- координаты
направляющего вектора, подлежащие определению.
Обозначим за ![]() точку кривой, ближайшую к точке асимптоты,
соответствующей значению параметра
точку кривой, ближайшую к точке асимптоты,
соответствующей значению параметра ![]() . Тогда координаты точки
. Тогда координаты точки
![]() равны
равны
Пусть ![]() - совокупность членов степени
- совокупность членов степени ![]() , входящих в
многочлен
, входящих в
многочлен ![]() . Тогда он может быть представлен в виде суммы
однородных компонент различных степеней:
. Тогда он может быть представлен в виде суммы
однородных компонент различных степеней:
Вычислим асимптоты кубической кривой
![]() Подстановка
параметрических уравнений асимптоты
Подстановка
параметрических уравнений асимптоты
![]()
![]() и выделение компонент старших степеней приводят к
уравнениям:
и выделение компонент старших степеней приводят к
уравнениям:
Если параметрическое задание кривой интерпретировать как
кинематическое описание движения материальной точки с течением
времени ![]() , то регулярность этого задания требует, чтобы вектор
мгновенной скорости
, то регулярность этого задания требует, чтобы вектор
мгновенной скорости
![]() не обращался в
нуль ни при каком значении
не обращался в
нуль ни при каком значении ![]() .
.
В этом случае длина кривой - это путь, пройденный материальной
точкой за промежуток времени
![]()
![$\displaystyle s_{[a,b]}=\int
\limits_a^b \vert\vec r '(t)\vert dt.$](img205.png)
В случае явного функционального задания ![]() кривой нетрудно
перейти к параметрическому заданию
кривой нетрудно
перейти к параметрическому заданию ![]()
![]() и получить
формулу
и получить
формулу
![$\displaystyle s_{[a,b]}=\int \limits_a^b\sqrt{1+f' ^2(x)}dx.
$](img208.png)
Пусть ![]() и
и ![]() - две различные точки кривой
- две различные точки кривой ![]() ,
, ![]() -
прямая, содержащая точку
-
прямая, содержащая точку ![]() .
.
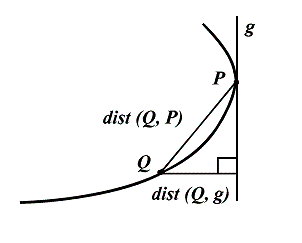
Касательной (рис. 13) к кривой ![]() в точке
в точке ![]() называется прямая
называется прямая ![]() , удовлетворяющая соотношению
, удовлетворяющая соотношению
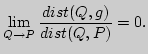
Уравнение касательной к кривой ![]() в ее точке
в ее точке ![]() может быть
вычислено одним из следующих способов (
может быть
вычислено одним из следующих способов (![]() - координаты точки
касательной):
- координаты точки
касательной):
| при | параметрическом задании 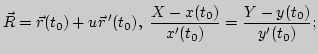 |
||
| при | явном функциональном задании |
||
| при | неявном задании |
| при | параметрическом задании |
||
| где вектор |
|||
или, в каноническом виде, 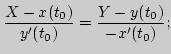 |
|||
| при | явном функциональном задании |
||
| при | неявном задании |
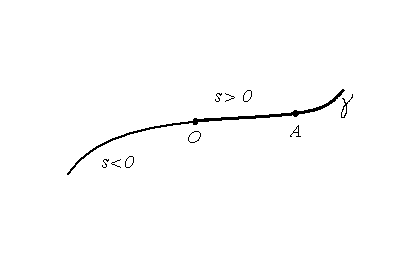
Зафиксируем на кривой ![]() (рис. 14) точку
(рис. 14) точку ![]() и одно из двух
возможных направлений. Тогда каждой точке
и одно из двух
возможных направлений. Тогда каждой точке ![]() кривой может быть
поставлено во взаимно однозначное соответствие число
кривой может быть
поставлено во взаимно однозначное соответствие число ![]() , равное
длине дуги
, равное
длине дуги ![]() , взятой со знаком "
, взятой со знаком "![]() ", если дуга
", если дуга ![]() расположена в зафиксированном направлении относительно точки
расположена в зафиксированном направлении относительно точки ![]() ,
и со знаком "
,
и со знаком "![]() " в противном случае. Указанное соответствие
поставляет параметризацию кривой, называемую естественной.
Параметр
" в противном случае. Указанное соответствие
поставляет параметризацию кривой, называемую естественной.
Параметр ![]() называется естественным параметром.
называется естественным параметром.
Несложно показать, что естественная параметризация кривой регулярна, причем
Пусть ![]() и
и ![]() - две различные точки кривой
- две различные точки кривой ![]() ,
соответствующие значениям
,
соответствующие значениям ![]() и
и
![]() естественного
параметра (рис. 15). Тогда
естественного
параметра (рис. 15). Тогда
![]() - длина дуги кривой,
заключенной между точками
- длина дуги кривой,
заключенной между точками ![]() и
и ![]() . Пусть
. Пусть
![]() -
величина ориентированного угла, образуемого касательной к кривой в
точке
-
величина ориентированного угла, образуемого касательной к кривой в
точке ![]() по отношению к касательной в точке
по отношению к касательной в точке ![]() .
.
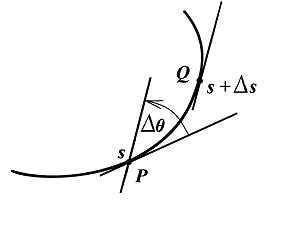
Кривизна кривой ![]() в ее точке
в ее точке ![]() - это предел
- это предел
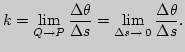
Будем интерпретировать естественную параметризацию
![]() кривой
кривой ![]() как кинематическое описание движения
материальной точки. Уравнение (4) означает, что это - равномерное
криволинейное движение с постоянной по модулю скоростью, равной
единице, то есть движение, при котором точка проходит в единицу
времени путь, равный единице длины. При этом направление скорости
может меняться. Модуль кривизны в этой интерпретации - это модуль
угловой скорости поворота вектора касательной к кривой при
движении по кривой с единичной скоростью.
как кинематическое описание движения
материальной точки. Уравнение (4) означает, что это - равномерное
криволинейное движение с постоянной по модулю скоростью, равной
единице, то есть движение, при котором точка проходит в единицу
времени путь, равный единице длины. При этом направление скорости
может меняться. Модуль кривизны в этой интерпретации - это модуль
угловой скорости поворота вектора касательной к кривой при
движении по кривой с единичной скоростью.
Заметим, что угол между касательными в точках ![]() и
и ![]() может быть
включен в соотношение
может быть
включен в соотношение
![]() тогда, используя первый
замечательный предел, нетрудно прийти к выражению
тогда, используя первый
замечательный предел, нетрудно прийти к выражению
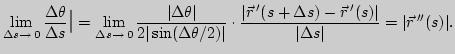
Задачи
1. Кривая задана в прямоугольной декартовой системе
координат явной функциональной зависимостью. Изобразите на рисунке
вид кривой. Укажите область изменения независимой координаты и
область регулярности задания кривой. Напишите задание этой кривой
а) в координатно-параметрической форме б) в
векторно-параметрической форме в) в неявной форме.
2. Кривая задана в полярной системе координат явной функциональной зависимостью. Изобразите на рисунке вид кривой. Укажите область изменения полярного угла и область регулярности задания кривой. Напишите задание этой кривой в прямоугольной декартовой системе координат в параметрической форме (координатной или векторной).
3. Кривая задана в прямоугольной декартовой системе координат
неявной функциональной зависимостью. Укажите области регулярности
этого задания кривой. Можно ли написать ее глобальное задание
а) явной функциональной зависимостью,
б) в параметрической форме?
Можно ли сделать то же самое локально в окрестности каждой
точки?
Постройте те из указанных заданий кривой, которые
возможны.
4. Кривая задана параметрическими уравнениями. Укажите область изменения параметра и области регулярности данного задания кривой.

5. Циклоида. По прямой без проскальзывания катится
окружность радиуса ![]() . На окружности зафиксирована точка (рис. 16
а)). Напишите параметрические уравнения траектории этой точки.
. На окружности зафиксирована точка (рис. 16
а)). Напишите параметрические уравнения траектории этой точки.
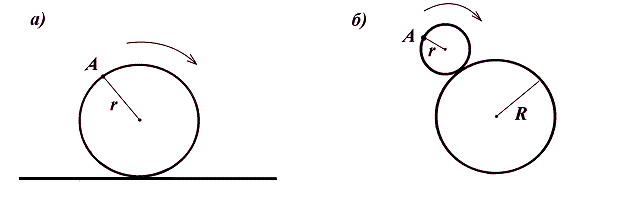
6. Эпи- и гипоциклоиды. По окружности радиуса ![]() катится
без проскальзывания окружность радиуса
катится
без проскальзывания окружность радиуса ![]() с отмеченной точкой,
оставаясь вне (внутри) большей окружности (рис. 16 б)). Напишите
параметрические уравнения траектории отмеченной точки.
с отмеченной точкой,
оставаясь вне (внутри) большей окружности (рис. 16 б)). Напишите
параметрические уравнения траектории отмеченной точки.
7. Вычислите уравнения асимптот данных кривых, заданных явной функциональной зависимостью в декартовых координатах:
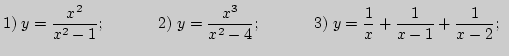
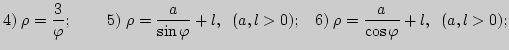
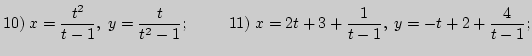
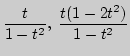 )
)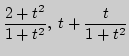 )
)
8. Кривая задана параметрически в прямоугольной декартовой системе
координат. Напишите уравнения касательной и нормали в точке
кривой, соответствующей значению параметра ![]() . Укажите
координаты единичного вектора касательной и единичного вектора
нормали в этой точке. Напишите уравнения семейства касательных и
семейства нормалей в регулярных точках данной кривой. Напишите
уравнение семейства единичных касательных векторов данной
кривой.
. Укажите
координаты единичного вектора касательной и единичного вектора
нормали в этой точке. Напишите уравнения семейства касательных и
семейства нормалей в регулярных точках данной кривой. Напишите
уравнение семейства единичных касательных векторов данной
кривой.
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
9. Найдите величину угла между кривыми в точке их пересечения.
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
10. Покажите, что касательная в любой точке кривой
![]() образует с полярным радиусом постоянный угол, и
вычислите его.
образует с полярным радиусом постоянный угол, и
вычислите его.
11. Покажите, что касательные к кардиоиде
![]() , проведенные в точках пересечения кардиоиды с хордами,
проходящими через полюс, перпендикулярны.
, проведенные в точках пересечения кардиоиды с хордами,
проходящими через полюс, перпендикулярны.
12. Покажите, что касательные к лемнискате Бернулли
![]() , проведенные в точках пересечения с
хордой, проходящей через полюс, параллельны.
, проведенные в точках пересечения с
хордой, проходящей через полюс, параллельны.
13. Покажите, что отрезок касательной к гиперболе ![]() ,
заключенный между осями координат, делится точкой касания пополам.
,
заключенный между осями координат, делится точкой касания пополам.
14. Покажите, что отрезок касательной к трактрисе
15. Вычислите длину дуги кривой
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
16. Для данных кривых найдите вид функции ![]()
![]()
![]() , в зависимости от способа задания кривой. Является
ли эта функция непрерывной? Монотонной? Дифференцируемой? С какими
фактами и теоремами геометрии и математического анализа это
связано?
, в зависимости от способа задания кривой. Является
ли эта функция непрерывной? Монотонной? Дифференцируемой? С какими
фактами и теоремами геометрии и математического анализа это
связано?
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
17. Вычислите кривизну данной кривой в заданной ее точке, сначала
используя готовую формулу, а затем по следующему плану: получите
уравнение поля скоростей при равномерном движении по этой кривой,
затем вычислите абсолютную величину его производной по "времени"
![]() .
.
1) ![]() в вершинах кривой; 2)
в вершинах кривой; 2)
![]()
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() 6)
6)
![]()
18. Кривизна - характеристика второго порядка. Разлагая задание
кривой в окрестности данной точки по формуле Тейлора с точностью
до второго порядка, получим задание кривой второго порядка,
которую назовем соприкасающейся параболой этой кривой в данной ее
точке. Вычислите кривизну кривой в данной точке, ее
соприкасающейся параболы в этой точке и сравните результаты.
1)
![]() ;
2)
;
2)
![]()
3)
![]() 4)
4)
![]()
Огибающая семейства плоских кривых, заданного
уравнением
![]() - это кривая, удовлетворяющая
системе уравнений
- это кривая, удовлетворяющая
системе уравнений
19. Парабола
безопасности. Из точки ![]() под всевозможными углами
под всевозможными углами
![]() к горизонту производятся выстрелы с начальной скоростью
снаряда
к горизонту производятся выстрелы с начальной скоростью
снаряда ![]() .
Найдите уравнение границы области, недостижимой для снарядов.
.
Найдите уравнение границы области, недостижимой для снарядов.