Вопросы теории
Пространственные кривые. Задание пространственной кривой.
Регулярное задание кривой. Регулярная кривая. Неявное задание
пространственной кривой. Касательная к пространственной кривой.
Единичный вектор касательной. Бинормаль и главная нормаль и их
единичные векторы. Нормальная, соприкасающаяся и спрямляющая
плоскости. Ускорение при криволинейном движении и векторы
сопровождающего трехгранника. Кривизна пространственной кривой.
Теорема о прямой. Кручение пространственной кривой. Теорема о
плоской кривой. Формулы Френе.
Естественный параметр и натуральные уравнения кривой.
Основные определения, результаты, комментарии
Элементарной кривой в пространстве называется образ
открытого интервала
![]() при его
гомеоморфизме
при его
гомеоморфизме
![]() в евклидово трехмерное
пространство.
в евклидово трехмерное
пространство.
Общей кривой на плоскости называется подмножество евклидова пространства, локально гомеоморфное прямой.
Как и в случае плоских кривых, всякая общая кривая допускает покрытие элементарными кривыми.
Кривая ![]() задана неявным способом
задана неявным способом
Наиболее удобны и наиболее часто используются векторно-параметрическое представление
Определение регулярности параметрического представления пространственной кривой полностью аналогично плоскому случаю.
Неявное задание (5) кривой регулярно в точке ![]() , если матрица
частных
производных
, если матрица
частных
производных
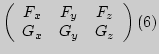
Понятия длины кривой, ее естественной параметризации, а также
определение касательной полностью аналогичны тем же понятиям для
плоских кривых. Направляющий вектор касательной - это,
по-прежнему, производная
![]() , имеющая физический смысл
скорости, если параметрическое представление кривой
интерпретировать как кинематическое описание движения точки.
, имеющая физический смысл
скорости, если параметрическое представление кривой
интерпретировать как кинематическое описание движения точки.
Нормальная плоскость кривой в точке ![]() - это плоскость,
проходящая через точку
- это плоскость,
проходящая через точку ![]() ортогонально касательной.
ортогонально касательной.
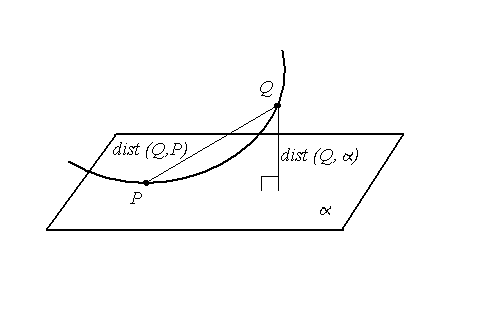
Соприкасающейся плоскостью кривой в ее точке ![]() (рис. 17)
называется содержащая эту точку плоскость
(рис. 17)
называется содержащая эту точку плоскость ![]() ,
удовлетворяющая соотношению
,
удовлетворяющая соотношению
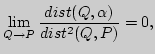
Спрямляющей плоскостью кривой в ее точке ![]() называется
содержащая эту точку плоскость, ортогональная нормальной и
соприкасающейся плоскостям в этой точке.
называется
содержащая эту точку плоскость, ортогональная нормальной и
соприкасающейся плоскостям в этой точке.
Прямые, ортогональные соприкасающейся и спрямляющей плоскостям в
точке ![]() , называются соответственно бинормалью и главной нормалью кривой в точке
, называются соответственно бинормалью и главной нормалью кривой в точке ![]() .
.
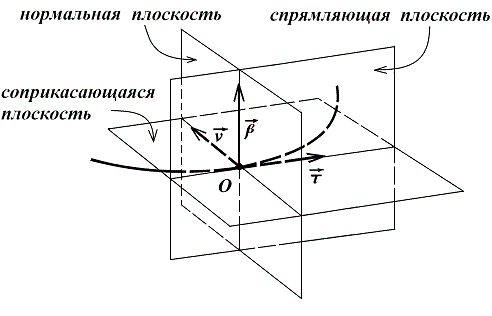
Нормальная, соприкасающаяся и спрямляющая плоскости образуют сопровождающий трехгранник кривой, или трехгранник Френе, в
точке ![]() , и называются его гранями. Касательная, бинормаль
и главная нормаль называются ребрами сопровождающего
трехгранника (рис. 18).
, и называются его гранями. Касательная, бинормаль
и главная нормаль называются ребрами сопровождающего
трехгранника (рис. 18).
Уравнения элементов сопровождающего трехгранника вычисляются по
следующим правилам:
| Касательная | Нормальная плоскость |
|
|
|
| Бинормаль | Соприкасающаяся плоскость |
|
|
|
| Главная нормаль
|
Спрямляющая плоскость |
|
|
|
| касательной |
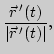 |
||
| главной нормали |
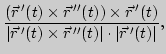 |
||
| бинормали |
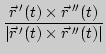 |
Если параметризация естественная, то вектор главной нормали
может быть вычислен по формуле
![]() .
.
Вектор ускорения может быть разложен в сумму двух составляющих: нормальной (ортогональной вектору скорости) и тангенциальной (параллельной вектору скорости). При этом нормальная составляющая ускорения сонаправлена единичному вектору главной нормали.
Пусть ![]() и
и ![]() - две различные точки кривой
- две различные точки кривой ![]() ,
соответствующие значениям
,
соответствующие значениям ![]() и
и
![]() естественного
параметра. Тогда
естественного
параметра. Тогда
![]() - длина дуги кривой, заключенной
между точками
- длина дуги кривой, заключенной
между точками ![]() и
и ![]() . Пусть
. Пусть
![]() - величина угла,
образуемого касательной к кривой в точке
- величина угла,
образуемого касательной к кривой в точке ![]() по отношению к
касательной в точке
по отношению к
касательной в точке ![]() . Кривизна кривой
. Кривизна кривой ![]() в ее точке
в ее точке
![]() - это предел
- это предел
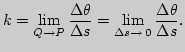
 |
|||
Пусть ![]() и
и ![]() - две различные точки кривой
- две различные точки кривой ![]() ,
соответствующие значениям естественного параметра
,
соответствующие значениям естественного параметра ![]() и
и
![]() соответственно,
соответственно,
![]() и
и
![]() -
единичные векторы бинормалей в этих точках (рис. 19).
-
единичные векторы бинормалей в этих точках (рис. 19).
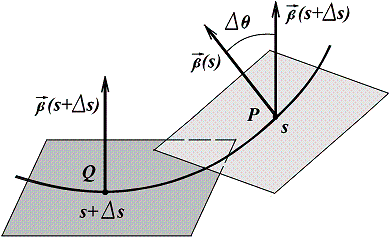
Обозначим за
![]() величину угла между ними. Очевидно,
этот угол равен углу, образованному соприкасающимися плоскостями в
точках
величину угла между ними. Очевидно,
этот угол равен углу, образованному соприкасающимися плоскостями в
точках ![]() и
и ![]() .
.
Абсолютным кручением кривой в точке ![]() называют величину
называют величину
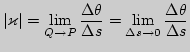
Кручение кривой ![]() определяется в соответствии со
следующим правилом:
определяется в соответствии со
следующим правилом:
![]() если при движении
вдоль кривой по направлению возрастания параметра вектор бинормали
если при движении
вдоль кривой по направлению возрастания параметра вектор бинормали
![]() поворачивается в сторону, указываемую вектором
поворачивается в сторону, указываемую вектором ![]() ,
,
![]() в противном случае. Наглядно это
означает, что кривая с положительным кручением "закручена" по
правилу правого винта.
в противном случае. Наглядно это
означает, что кривая с положительным кручением "закручена" по
правилу правого винта.
Кручение кривой в точке, соответствующей значению параметра ![]() ,
может быть вычислено по следующим формулам:
,
может быть вычислено по следующим формулам:
 |
|||
 |
Для производных векторов
![]()
![]() ,
,
![]() по
естественному параметру справедливы формулы Френе:
по
естественному параметру справедливы формулы Френе:
Уравнения ![]() и
и
![]() называются натуральными уравнениями кривой. По натуральным уравнениям вид
кривой может быть восстановлен с точностью до перемещения. В
большинстве случаев решение такой задачи оказывается очень
сложным.
называются натуральными уравнениями кривой. По натуральным уравнениям вид
кривой может быть восстановлен с точностью до перемещения. В
большинстве случаев решение такой задачи оказывается очень
сложным.
Задачи
1. Для данных представлений кривых укажите область допустимых
значений параметра и область значений параметра, в которой задание
кривой регулярно.
1)
![]()
2)
![]()
3)
![]()
4)
![]() .
.
2. Кривая задана неявными уравнениями. Изобразите на рисунке вид
кривой. Постройте какое-нибудь параметрическое представления этой
кривой. Укажите область допустимого изменения параметра и область
регулярности
параметризации.
1)
![]()
2)
![]()
3)
![]()
3. Кривая Вивиани образована пересечением сферы радиуса ![]() и цилиндра радиуса
и цилиндра радиуса ![]() , проходящего через центр сферы. Постройте
параметрическое представление кривой Вивиани.
, проходящего через центр сферы. Постройте
параметрическое представление кривой Вивиани.
4. Винтовая линия. Окружность радиуса ![]() движется так, что
ее центр перемещается вдоль оси
движется так, что
ее центр перемещается вдоль оси ![]() , плоскость ортогональна оси
, плоскость ортогональна оси
![]() . По окружности равномерно движется точка. В начальный момент
времени
. По окружности равномерно движется точка. В начальный момент
времени ![]() точка имеет координаты
точка имеет координаты ![]() . Составьте
параметрические уравнения кривой, описываемой данной точкой.
. Составьте
параметрические уравнения кривой, описываемой данной точкой.
5. Кривая ![]() задана пересечением цилиндрических поверхностей
задана пересечением цилиндрических поверхностей
![]() и
и ![]() Постройте параметрическое представление
кривой
Постройте параметрическое представление
кривой ![]() , не содержащее радикалов, и дайте ее изображение.
, не содержащее радикалов, и дайте ее изображение.
6. Покажите, что линия
7. Найдите длину дуги линии
8. Покажите, что кривая
![]() замкнута и имеет длину
замкнута и имеет длину ![]() .
.
9. Запишите в естественной параметризации
a) винтовую линию
![]() ;
;
б) гиперболическую винтовую линию
![]() .
.
10. Кривая задана параметрически:
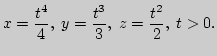
11. Найдите линию, по которой касательные к линии
Сферической индикатрисой данной кривой называется геометрическое место концов единичных касательных векторов, отложенных от начала координат.
12. Дана винтовая линия
13. Докажите, что все нормальные плоскости кривой Вивиани (задача 3) проходят через начало координат.
14. Составьте уравнения бинормали и главной нормали кривой в
указанной точке:
1)
![]()
2)
![]()
3)
![]() ;
;
4)
![]()
15. Найдите точки на кривой
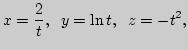
16. Материальная точка движется в пространстве по закону
17. Составьте уравнения ребер и граней сопровождающего
трехгранника данной кривой в указанной точке
1)
![]()
2)
![]()
3)
![]()
4)
![]()
18. Для данной кривой вычислите кривизну в данной точке сначала по
готовой формуле, а затем по следующему плану: 1) составьте
уравнение поля единичных касательных векторов данной кривой; 2)
вычислите абсолютную величину производной этого поля по
естественному
параметру. Результаты сравните.
1)
![]()
2)
![]()
19. Для кривых задачи 18 вычислите абсолютное кручение в данной точке сначала по готовой формуле, а затем по следующему плану: 1) составьте уравнение поля единичных векторов бинормали данной кривой; 2) вычислите абсолютную величину производной этого поля по естественному параметру. Результаты сравните.
20. Вычислите кривизну и кручение данной кривой произвольной
регулярной точке:
1)
![]() ;
;
2)
![]()
3)
![]()
4)
![]() .
.
21. Найдите точки распрямления следующих кривых:
1)
![]()
2)
![]()
3)
![]() .
.
22. Найдите точки уплощения и дуги, на которых кручение сохраняет
свой знак, у следующих кривых:
1)
![]()
2)
![]()
23. Напишите натуральные уравнения, которым удовлетворяют
следующие кривые:
1)
![]() ;
;
2)
![]()
24. Найдите точки на кривой
25. Найдите точки на кривой
26. Докажите, что следующие кривые плоские, и составьте уравнения
плоскостей, в которых они расположены:
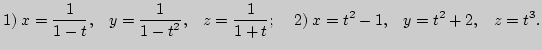
27. Найдите такую функцию ![]() , чтобы кривая
, чтобы кривая
28. Докажите, что если все соприкасающиеся плоскости линии
проходят через неподвижную точку ![]() , то линия плоская.
, то линия плоская.
29. Докажите, что если соприкасающиеся плоскости линии (отличной
от прямой) параллельны некоторому вектору ![]() , то линия
плоская.
, то линия
плоская.
30. Докажите, что если все нормальные плоскости линии параллельны
некоторому вектору ![]() , то линия или прямая, или плоская.
, то линия или прямая, или плоская.