Далее: Дидактический модуль "Введение в
Вверх: Теоретические основы наглядного моделирования
Назад: §3. Педагогический процесс наглядно-модельного
В основе инновационного подхода к отбору содержания предметной
подготовки учителя математики лежит овладение когнитивным стилем
профессиональной деятельности посредством актуализации
субъективного опыта в процессе освоения теоретического обобщения
БУЭШМ на основе процессов фундирования и наглядного
моделирования.
Педагогическая технология представляет собой существо совместной
деятельности преподавателя и студента, ведущей к достижению
планируемых результатов. В то же время методическое оформление
сути технологического процесса придает технологии гибкость и
определяется, в частности, как содержанием учебной информации,
так и педагогическим мастерством преподавателя.
Выделяя в педагогическом процессе обучения математике три
процессуальных компонента: учебную деятельность, обучающую
деятельность и взаимодействие, особое внимание будем уделять
проектированию и организации деятельности студента. Существенным
при этом является то, что обучающая деятельность опосредована
учебной деятельностью, активностью и личностными качествами
студента и направлена на всестороннее развитие личности в
соответствии с идеей личностно-ориентированного подхода. Учебная
деятельность при этом предполагает развертывание процессов (в
соответствии с динамической структурой личности) в трех
обозначенных выше направлениях:
| Направления |
Состав деятельности |
Содержание |
Формы |
|
|
|
(структуры математики) |
|
 объектно-сущ- объектно-сущ-
ностное (приобретение опыта) |
Формирование когнитивного
опыта личности путем раскрытия
внутренних существенных связей объекта изучения, выделение
ба-
зисных учебных элементов и
определение их иерархий, свертывание
и развертывание ООУД |
 топологические, топологические,
 алгебраические, алгебраические,
 порядковые, порядковые,
 вероятностные, вероятностные,
 геометрические (кривые, поверхности, графы), геометрические (кривые, поверхности, графы),
 функциональные (мера, производная, интеграл, ряд) функциональные (мера, производная, интеграл, ряд) |
Опорные таблицы ЗУНМА,
аннотированные учебные программы,
интегрированные экзаменационные программы, дидактические модули,
спирали фундирования, содержательные блоки, учебные предметы и
дисциплины, банки задач, историко-методическое оснащение учебного
предмета,
структурный анализ базовых
учебных элементов (школьной
и вузовской математики), актуализация технологий
профессионально-математической
деятельности, цепочки задач
научно-исследовательского характера, мотивационные блоки |
 деятельностно- деятельностно-
результативное (применение и
преобразование опыта) |
Процесс применения и преобразования ментального опыта личности в
виде ком-
плекса внешних и
внутренних действий, увязывающих новую
информацию (знания) с наличным репертуаром памяти и усво-
енными
стереотипами деятельности, направленный на по-
лучение конкретных
результатов на основе ИОУД |
 логические (кванторы, предикаты,
доказательства,
формулы), логические (кванторы, предикаты,
доказательства,
формулы),
 знаково-символические (алфавит, индексы и символы,
языковые знаки), знаково-символические (алфавит, индексы и символы,
языковые знаки),
 реляционные (таблицы, графики), реляционные (таблицы, графики),
 продукционные (алго- продукционные (алго-
ритмы, процедуры, математические
методы),
 семантические (блок- семантические (блок-
схемы, теоремы, определения) |
Алгоритмико-вычисли- тельные процессы, деловые и имитационные игры,
выполнение курсовых, дипломных, лабораторных работ, построение
геометрических объектов, доказательство теорем, решение уравнений
и неравенств, наглядное моделирование, тождес-
твенные
преобразования, взаимопереходы знаковых систем |
 личностно- личностно-
адаптационное (развитие личност-
ных характеристик и интеллекта) |
Диагностируемое целеполагание, прогнозирование и принятие
решения, способность к обнаружению и постановке проблемы, анализ
данных и мобилизация информации, рефлексия и оценочная
деятельность, анализ и синтез, обобщение и конкретизация,
аналогии и ассоциации |
 преемственность школьных и вузовских знаний, умений,
математических методов, идей и процедур, преемственность школьных и вузовских знаний, умений,
математических методов, идей и процедур,
 содержательное обобщение базовых школьных учебных
элементов, содержательное обобщение базовых школьных учебных
элементов,
 внутренняя интерпретируемость, структурирован- внутренняя интерпретируемость, структурирован-
ность, связность, актив-
ность и целостность профессиональных проб и
опыта,
 освоение структуры и состава ООУД, освоение структуры и состава ООУД,
 развитие когнитивных и развитие когнитивных и
креативных структур,
про-
фессионально важных и
значимых качеств, педагогического и
математического мышления |
Педагогическая и стажерская практики |
Наиболее адекватной формой и средством развертывания
дидактических процессов фундирования и наглядного моделирования
является структура дидактического модуля.
Дидактический модуль, являясь целостной структурой совместной
деятельности учителя и ученика в процессе решения педагогических
задач, может быть исследован также как компонент педагогической
системы деятельности и, более того, психологической системы
деятельности ученика. С точки зрения деятельностной теории
учения [32], дидактический модуль должен также содержать
ориентировочную, исполнительскую и контрольно-коррекционную
части. Это определяет три основных компонента дидактического
модуля (ДМ):
 ориентировочную основу деятельности (как учителя, так и
ученика);
ориентировочную основу деятельности (как учителя, так и
ученика);
 информационную основу деятельности (как учителя, так и
ученика);
информационную основу деятельности (как учителя, так и
ученика);
 блок управления учителем когнитивной деятельности
ученика.
блок управления учителем когнитивной деятельности
ученика.
Первый блок содержит:
 введение (описание структуры и состава деятельности,
особенности учебного предмета);
введение (описание структуры и состава деятельности,
особенности учебного предмета);
 базу данных и базу знаний, необходимых для усвоения
нового материала (преемственность деятельности);
базу данных и базу знаний, необходимых для усвоения
нового материала (преемственность деятельности);
 аннотированную учебную программу, детализированную по
уровням усвоения знаний, ступеням абстракции, мотивации и
продуктивности учебной деятельности (развернутость содержания);
аннотированную учебную программу, детализированную по
уровням усвоения знаний, ступеням абстракции, мотивации и
продуктивности учебной деятельности (развернутость содержания);
 локальные фрагменты (и их динамика) пластов спиралей
фундирования, необходимо содержащие школьный
(профессионально-направленный) и мотивационный компонент
(обобщенность деятельности);
локальные фрагменты (и их динамика) пластов спиралей
фундирования, необходимо содержащие школьный
(профессионально-направленный) и мотивационный компонент
(обобщенность деятельности);
 интегративную экзаменационную программу
(интегративные
интегративную экзаменационную программу
(интегративные
ЗУНМА, творческие задания, общеучебные умения,
профессионально-математический базис) как свернутость
деятельности и условие для преемственности ДМ.
Требования к проектированию дидактического модуля включают в
себя: преемственность содержательных линий школьной и вузовской
математики; использование современных форм представления знаний
(логической, реляционной, семантической, продукционной,
фреймовой); развертывание и свертывание спиралей фундирования
базовых учебных элементов школьной математики; блоки
мотивационно-прикладных задач, оснащающих спирали фундирования, и
др. Компонентный состав дидактического модуля представлен на
следующем рисунке:
![\begin{picture}(160.00,207.00)
\put(80.00,204.00){\makebox(0,0)[cc]{Введение}}
\...
....00}{188.00}{306}
\emline{72.00}{174.00}{307}{102.00}{174.00}{308}
\end{picture}](img83.png)
Рис. 17. Компоненты ДМ учебного предмета: ЛК - лекционный
курс; ПК - практический курс; ЛЗ - лабораторные
занятия; СР - самостоятельная работа; К/Р - контрольная
работа; ДК/Р - домашняя контрольная работа;
ППП - педагогический программный продукт;
НИР - научно-исследовательская работа;
КЛ - коллоквиум; 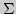 - итого
- итого
Схема
методики изучения раздела математики
(лекция, практическое занятие, тема, дисциплина и т.п.)
![\begin{picture}(161.00,130.00)
\put(78.00,125.00){\makebox(0,0)[cc]{Исходное сос...
...0){\vector(4,-1){19.00}}
\put(112.00,72.00){\vector(-4,-1){19.00}}
\end{picture}](img85.png)
Незамкнутость методических параметров обратной связи на блок
исходного состояния личности студента означает возможность
вариативности методики в зависимости от интеллектуальных и
личностных качеств студента. Это означает необходимость создания
психологической службы при факультетах с целью мониторинга
динамики функционирования личностной сферы каждого студента, а
также повышения качества психолого-педагогической подготовки
преподавателя с целью профессиональной готовности к
психологической дифференциации обучения математике.
При этом деятельностный модуль определяет проектирование
учебной деятельности студентов, целью и результатами которой
является получение конкретных проявлений и конкретизаций
математических понятий, утверждений, процедур и алгоритмов,
выраженных упорядоченными наборами чисел и простейших
геометрических объектов.
Определение и наглядное моделирование ориентировочной
основы
учебной деятельности (ООД) в процессе
обучения математике и предъявление ее обучаемому создает
положительную мотивацию учения диагностируемого уровня. В основе
такого подхода лежит методологический тезис А.Н.Леонтьева: "...актуально
сознается только то содержание, которое является предметом
целенаправленной деятельности студента, т.е. занимает структурное место
непосредственно цели внутреннего или внешнего действия в системе той
или иной деятельности".
ООУД представляет собой свернутую структурированную модель
(дидактический модуль) содержания учебной деятельности,
адекватно отражающую динамику и логику развертывания учебного
содержания
(учебных элементов) реального педагогического
процесса, включающую таксономию учебных целей и спирали
фундирования.
Процессуальная структура дидактического процесса обучения
математике представлена на следующем рисунке:
![\begin{picture}(162.00,100.00)
\put(15.00,97.00){\makebox(0,0)[cc]{\bf Педагогич...
...00){\vector(0,-1){13.00}}
\put(144.00,41.00){\vector(0,-1){13.00}}
\end{picture}](img86.png)
Рис. 18.
Обогащенная дидактическая система
Блок исходных характеристик
Процесс обучения математике (например, математическому анализу)
предполагает последовательное изучение заранее
обусловленных разделов:
число, функция, последовательность,...,
основные теоремы дифференциального исчисления,...
Этот перечень, по существу, дается аннотированной учебной программой (по
математическому анализу) и может быть представлен схемой
![\begin{picture}(124.00,30.00)
\put(25.00,20.00){\framebox (9.00,10.00)[cc]{$\dow...
...){\makebox(0,0)[cc]{$X$}}
\put(124.00,20.00){\makebox(0,0)[cc]{,}}
\end{picture}](img87.png)
причем каждая тема 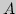 ,
, 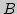 ,
, 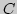 ,...,
,..., 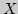 представлена блоком, а ее прохождение - стрелкой.
Здесь
представлена блоком, а ее прохождение - стрелкой.
Здесь 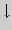 означает переход от простого к сложному, от
знания неполного к более полному, причем
означает переход от простого к сложному, от
знания неполного к более полному, причем
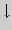 означает не только логическое строение
данного материала, но и превалирующее направление формирования
понятий, умений и практических навыков.
Однако в процессе преподавания естественно
приходится устанавливать и проявлять внутренние взаимосвязи
между блоками
означает не только логическое строение
данного материала, но и превалирующее направление формирования
понятий, умений и практических навыков.
Однако в процессе преподавания естественно
приходится устанавливать и проявлять внутренние взаимосвязи
между блоками
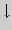 |
;
среди этих взаимосвязей есть существенные, основные, которые,
будучи упорядоченными, образуют сквозные связи между блоками,
объединенные той или иной сквозной темой,
материализацией которых выступает спираль фундирования.
Последние же цементируют учебный материал,
способствуя дидактическим целям и являясь внешними опорами
восприятия обучаемых.
В то же время выявление сквозных тем в качестве
существенных внутренних взаимосвязей позволяет активизировать
память студентов, варьируя следы предыдущих знаний
(остаточные фреймы) в процессе обучения математике.
Выделение, систематизация и реализация сквозных тем
(а также спиралей фундирования)
в курсе математического
анализа имеют явную профессионально-педагогическую
направленность,
поскольку единство математики в реализации
сквозной темы выступает прежде всего единой формой теоретического
обобщения школьных учебных элементов
(предел, производная, непрерывность,...),
которая затем конкретизируется, выстраиваясь в
дидактически оправданную логическую цепь.
Последовательное и настойчивое проведение этой идеи
в процессе обучения формирует у будущих учителей
важное профессиональное умение - видеть за единой формой
базового учебного элемента вузовской математики
разнообразное содержание, объединенное единой логической основой.
Процесс кодирования базовых учебных элементов приводит к понятию
опорной таблицы кодировки (ОТК). ОТК - это проектирование
в форме семантической сети в свернутом виде содержания и
структуры базовых учебных элементов учебной дисциплины,
актуализирующихся и объективизирующихся в процессе освоения
математической деятельности. Состав кодируемых учебных элементов
отличается от традиционных ЗУНов (знания, умения, навыки): это
ЗУНМА - знания, умения, навыки, математические методы, алгоритмы
и процедуры. Каждый компонент ОТК должен быть раскодирован в
соответствии с АУП. На следующем рисунке представлена опорная таблица
кодировки базовых учебных
элементов ДМ-2 учебного предмета "Стохастика":
Таблица 3
Опорная таблица курса "Стохастика" (I семестр)
![\begin{picture}(159.00,230.00)
\put(80.00,227.00){\makebox(0,0)[cc]{ОСНОВНЫЕ}}
\...
...}{120.00}{19.00}{32}
\emline{114.00}{14.00}{33}{119.00}{19.00}{34}
\end{picture}](img92.png)
![\begin{picture}(159.00,131.00)
\put(80.00,128.00){\makebox(0,0)[cc]{ОСНОВНЫЕ}}
\...
...40.64}{14.62}{22}
\put(137.00,29.00){\makebox(0,0)[cc]{$\Omega $}}
\end{picture}](img93.png)
К основным компонентам, характеризующим состав ориентировочной
основы учебной деятельности студента, отнесем:
- базовые знания, умения, навыки, математические методы,
процедуры и алгоритмы (ЗУНМА);
- база данных спиралей фундирования, оснащенных
мотивационно-прикладными задачами;
- аннотированная учебная программа ЗУНМА, конкретизированная:
а) по 3 уровням усвоения учебных элементов;
б) по функциональным компонентам содержания (теоретический,
практический, прикладной, деятельностный, эвристический,
гуманитарный);
- историко-методическое оснащение базовых учебных элементов;
- основные компоненты, методика и измерители оценочной
деятельности;
- интегративная экзаменационная программа.
Технологические компоненты ДМ
Структура и состав ориентировочной основы учебной деятельности
студентов в освоении учебного предмета представлен в следующей
последовательности технологических компонентов:
Первый компонент
I. Состав
- Базовые знания, умения, навыки, математические методы,
алгоритмы и процедуры (для каждого дидактического модуля)
![\begin{picture}(120.00,27.00)
\put(20.00,18.00){\makebox(0,0)[cc]{+}}
\emline{17...
...18.00){\circle{5.66}}
\put(120.00,27.00){\makebox(0,0)[cc]{(OTK)}}
\end{picture}](img94.png)
Структура.
Свернутое и закодированное содержание
обучения в ОТК может развертываться также в четырех сферах:
- исходные характеристики как когнитивная основа для
освоения нового социального опыта в рамках дидактического модуля
(ДМ);
- базовые характеристики как проекция содержания АУП;
- интегративные характеристики как отражение свернутого результата
освоения нового когнитивного опыта в рамках ДМ;
- дидактические директивы как комплекс правил и
предписаний обобщенного характера, определяющих направления и
процедуры по достижению учебных целей.
Основная функциональная роль ОТК состоит в содействии
формированию устойчивых внутренних опор в ходе освоения учебного
содержания.
![\begin{picture}(140.00,41.00)
\put(31.00,37.00){\makebox(0,0)[cc]{Опорная таблиц...
...7.00){\vector(2,-1){30.00}}
\put(70.00,22.00){\vector(0,-1){9.00}}
\end{picture}](img95.png)
Следующие дидактические правила (директивы) отражают существо технологии
наглядного моделирования и сквозные, универсальные, существенные
требования к управлению базовыми учебными элементами.
- Правило 1.
- Математическое знание должно рассматриваться в
динамике взаимоперехода знаковых систем
по возможности в четырех сферах: знаково-символической,
вербальной, графической и деятельностной.
- Правило 2.
- Математическое знание должно проявляться не
менее чем в 10 конкретизациях (5 качественных).
- Правило 3.
- Математическое знание предполагает логический анализ содержания и формы.
- Правило 4.
- Мотивационная сфера математического знания
должна быть материализована 2-3 модельными задачами (в том
числе для спиралей фундирования).
- Правило 5.
- Математическое знание должно проявляться как часть более общего целого знания, в котором оно имеет свои
особенности, ограничения и форму.
- Правило 6.
- Математическое знание должно рассматриваться
в генезисе своего становления, во взаимосвязи с
историческим аспектом формы и содержания.
- Правило 7.
- Математическое знание должно иметь форму
представления посредством числа (действительного или
комплексного), геометрической фигуры.
Второй компонент
II. Состав
База данных спиралей фундирования, оснащенных
мотивационно-прикладными задачами (СФ). Компонентный состав и
структура спирали фундирования базового учебного элемента
представлены во фреймовой форме на следующем рисунке:
![\begin{picture}(159.00,122.00)
\put(133.00,117.00){\makebox(0,0)[rc]{Фрейм}}
\pu...
...43.00}{60.00}{192}
\emline{143.00}{66.00}{193}{157.00}{66.00}{194}
\end{picture}](img96.png)
Рис. 19.
Фрейм
представления теоретического обобщения школьного знания
(спираль фундирования)
Структура
|
Банк спиралей |
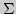 |
|
1 |
Понятия |
6-7 |
|
2 |
Теоремы |
4-5 |
|
3 |
Алгоритмы |
3-4 |
|
4 |
Процедуры |
2-3 |
|
Банк мотивационных |
|
задач |
|
По 1-2 на каждый |
|
компонент |
![\begin{picture}(114.00,65.00)
\put(80.00,62.00){\makebox(0,0)[cc]{Схема динамики...
...00}{6.00}{14}
\put(48.00,3.00){\dashbox{4.00}(64.00,51.00)[cc]{ }}
\end{picture}](img97.png)
Третий компонент
III. Состав
- Аннотированная учебная программа (АУП)
![\begin{picture}(158.00,76.00)
\put(3.00,73.00){\makebox(0,0)[lc]{1.}}
\put(18.00...
...makebox(0,0)[lc]{- компонент школьных знаний(профессиональных).}}
\end{picture}](img98.png)
Структура
![\begin{picture}(142.00,95.00)
\put(80.00,92.00){\makebox(0,0)[cc]{ЗУНМА}}
\put(8...
...0}{103}{67.00}{44.00}{104}
\put(64.00,41.00){\makebox(0,0)[rc]{Г}}
\end{picture}](img99.png)
Компоненты: *) теоретический (Т), прикладной (П),
практический (ПК), эвристический (Э), деятельностный (Д),
гуманитарный (Г)
Четвертый компонент
IV. Состав
- Интегративная экзаменационная программа (ИЭП)
Общая схема структурирования интегративных учебных элементов из
аннотированной учебной программы показана ниже:
Реализация целей и задач учебной деятельности студентов всецело
определяется требованиями к средствам управления их
познавательной деятельностью: методическими приемами,
дидактическими правилами, образцами деятельности, материальными и
информационными ресурсами. Например,
приемы локального моделирования включают: оперативную
наглядность, кодирование знаково-символических средств,
определение мотивационных блоков, построение семантических и
реляционных сетей, структурных блок-схем, логический анализ
теорем и структурный анализ понятий.
Структура. Требования
![\begin{picture}(147.00,44.00)
\put(20.00,44.00){\makebox(0,0)[cc]{АУП}}
\put(20....
...0,0)[cc]{ДМ$_i$}}
\put(130.00,3.00){\makebox(0,0)[cc]{ДМ$_{i+1}$}}
\end{picture}](img101.png)
*) К/Л - коллоквиум, Л/З - лабораторные занятия, ППП -
педагогические программные продукты,..., ДМ - дидактический
модуль
Пятый компонент
V. Состав
- Историко-методическое оснащение базовых учебных
элементов (БУЭ).
1 час ИМО на 10 часов аудиторных занятий.
- Формы:
- рефераты, самостоятельные работы,
учебно-исследовательские задачи, работа в малых группах,
профессиональные пробы, историко-математические экскурсы и т.п.
Структура
Требования
- элементы историзма и генезиса УЭ;
- отбор базовых и интегративных УЭ;
- взаимопереходы знаковых систем;
- решение задач при ограничении условий (поиск оптимальных
условий);
- вариативность способов решения задач;
- структурный анализ УЭ;
- единичное и особенное проявлений теорий учения в моделировании
процессов усвоения УЭ;
- актуализация фаз и типов ориентировки и исполнения в учебной
деятельности;
- формирование культуры устной и письменной речи, мышления;
- фундирование опыта и личностных характеристик в направлении
профессионализации;
- опора на устойчивые ассоциации, активизация ментальных и
личностных характеристик.
Основные ЗУНМА являются объектом для целостного изучения
наглядным моделированием (структурный анализ, сущность и явление,
спирали фундирования, уровни усвоения, историко-методическое
оснащение) в составе теоретического, практического, прикладного,
мотивационного, деятельностного и эвристического компонента.
При этом в соответствии с критерием полноты и оптимальности
базовые ЗУНМА школьной математики становятся основным исходным
звеном содержания учебных элементов профессионального блока
(I-III семестры). Базовые ЗУНМА вузовской математики
проектируются с возможностью логического расширения базового блока
до полного объема учебных предметов и покрытия базового блока
школьной математики.
Учебный предмет в структуре дидактического процесса
Глобальным компонентом дидактической системы является банк
учебных предметов, образующий сквозную (в течение всех лет
обучения) и содержательную целостность. Каждый учебный предмет
определяет набор учебных дисциплин, включая теорию и методику
обучения предмету, на весь период математического образования,
например:
| |
|
| Учебный предмет |
Учебные дисциплины |
| |
|
| |
|
| Математический анализ |
1.Дифференциальное и интегральное исчисление 1 переменного.
2. Дифференциальное и интегральное исчисление нескольких
переменных.
3. Ряды.
4. Дифференциальные уравнения.
5. Теория функций действительного и комплексного переменного.
6. Теория и методика обучения математическому анализу. |
| |
|
Учебный предмет, представляя собой целостную структуру учебной
информации в составе теоретического, практического, прикладного,
деятельностного, эвристического и гуманитарного компонентов,
содержательно развертывается в базисном, процессуальном и
иерархическом уровнях в своих локальных, модульных и глобальных
проявлениях. При этом целостность и направленность дидактической
системе придает развертывание спиралей фундирования базовых
учебных элементов школьной математики (БУЭШМ) в рамках учебного
предмета посредством построения родового теоретического обобщения
и технологического (и методического) осмысления видовых его
проявлений. Фрейм учебного предмета представлен на следующем
рисунке.
![\begin{picture}(160.00,84.00)
\put(108.00,80.00){\makebox(0,0)[rc]{\small Учебны...
...,23.00){\vector(1,3){9.00}}
\put(133.00,38.00){\vector(1,2){7.00}}
\end{picture}](img102.png)
Рис. 20. Фрейм учебного предмета
Предъявление спирали фундирования сопровождается развертыванием так называемого
мотивационного блока, состоящего из системы прикладных и профессионально
ориентированных задач, определяющих стимулирование познавательного
интереса обучаемых.
Фреймовое представление целостной схемы фундирования учебных
элементов позволяет
определить компонентный и процессуальный состав теоретического
обобщения базового школьного знания.
Блок функционирования и управления
Приемы локального фундирования и моделирования включают: оперативную и фоновую
наглядность в процессе усвоения математического материала, кодирование
знаково-символических средств представления математических знаний,
определение мотивационных блоков для освоения и развертывания
спиралей фундирования, построение семантических и
реляционных сетей, структурных блок-схем для актуализации
сущности математических объектов, логический анализ
теорем и структурный анализ понятий.
Ниже показаны методические приемы наглядного моделирования фоном
и семантической сетью базовых теорем математического анализа.
Фрейм теоремы
![\begin{picture}(157.00,102.00)
\put(154.00,98.00){\makebox(0,0)[rc]{Фрейм}}
\put...
...{157.00}{102.00}{54}
\emline{157.00}{102.00}{55}{1.00}{102.00}{56}
\end{picture}](img103.png)
Как уже отмечалось ранее, целостность процесса восприятия целевой
установки в процессе обучения математике является функциональной
характеристикой возрастных и личностных особенностей обучаемых.
При этом объектом восприятия (равно как и категории целостности)
может выступать как математическое знание, умения или действие,
так и процесс обучения математике или его этапы, фрагменты.
Целостность объекта восприятия еще не означает появления в
процессе обучения математике целостного субъективного образа в
мышлении обучаемого. В самом деле, в курсе математического
анализа много логически стройных, адекватных по сложности
изучаемому материалу, важных по применимости, задействованных
методов исследования (логические модели) и, таким образом,
целостных доказательств различных теорем, однако не наглядных по
сути существующих приемов и методов обучения. Это подтверждается
нашими многолетними наблюдениями за успешностью и адекватностью
воспроизведения указанных умений на экзаменах по математическому
анализу.
Например, использование структурной наглядности (семантическая
сеть) в представлении знаний применительно к доказательству
формул Тейлора (см. схему ниже) позволило добиться 70-75%
адекватного и осмысленного воспроизведения доказательства в
экспериментальной группе с вероятностно гарантированным
результатом.
Схема 9
Структурная схема
доказательства формулы Тейлора
![\begin{picture}(158.00,121.00)
\put(80.00,116.00){\makebox(0,0)[cc]{$f(x_0+h)=f(...
...{85}{80.00}{52.00}{86}
\emline{24.00}{40.00}{87}{24.00}{39.00}{88}
\end{picture}](img104.png)
Логический анализ теоремы может включать: логическую запись
формулировки теоремы, формулировки обратной и противоположной
теоремы, метод доказательства, блок-схему доказательства,
контрпримеры к условиям теоремы с графическими иллюстрациями и
т.п.
Основные понятия и теоремы тщательно и всесторонне
обсуждаются: проводится структурный анализ по следующей схеме:
Схема 10
Структурный анализ учебного элемента
![\begin{picture}(155.00,62.00)
\put(5.00,55.00){\framebox (40.00,7.00)[cc]{Истори...
...{45}{60.00}{18.00}{46}
\emline{80.00}{25.00}{47}{80.00}{18.00}{48}
\end{picture}](img105.png)
Методика работы в малых группах (опережающее отражение). В
процессе формирования приемов учебной деятельности в различных
формах коммуникации (лекции, практические и лабораторные занятия,
оценивание, компьютерный контроль, деловые игры, самостоятельная
работа и т.д.) у группы студентов стихийно выделяются
неформальные лидеры. Эти студенты обладают чуть большими по
сравнению с окружающими способностями к восприятию нового
учебного материала, чуть более обширными общеучебными навыками и
коммуникативными качествами, чуть более высоким интеллектуальным
потенциалом. Опыт преподавания показывает, что вокруг лидера
формируется коллектив (малая группа в 3-4 человека, иногда 2
студента), который стихийно вырабатывает общие унифицированные
приемы поведения, организует эффективный обмен идеями и образцами
деятельности, оптимизирует вклад каждого члена в достижение
учебных целей. Эта "фракционная" деятельность студентов постоянно
входит в противоречие с традиционными методами контроля,
организации творческой деятельности и самостоятельной работы.
Здесь предлагается методика эффективного использования потенциала
малых групп для более качественного усвоения знаний, формирования
творческой активности студентов, развития профессионально важных
качеств личности будущего учителя математики:
1. По прошествии небольшого числа (6-8) практических занятий на
I курсе (процесс формирования коллектива) преподаватель
определяет 6-7 малых групп (по итогам наблюдения) по 2-4
студента, достаточно подвижных по своему составу, и фиксирует
ситуацию, объявляя состав малых групп и установку на дальнейшую
совместную деятельность.
2. График учебного процесса и виды учебной деятельности
(самостоятельные контрольные работы на 10-15 минут, творческие
задания, домашние контрольные работы, контроль в дисплейном
классе, лабораторные занятия и т.п.) планируются a priori с
дифференциацией и вариативностью на 7 блоков с общей
ответственностью и результатом в малой группе. Эта методика не
касается проведения текущих контрольных работ (2-х часовых) и
зачетно-экзаменационных мероприятий, которые ориентированы на
индивидуальную ответственность студента.
3. Практическое занятие проводится по следующей схеме (ПК -
практические занятие):
![\begin{picture}(158.00,120.00)
\put(86.00,115.00){\makebox(0,0)[lc]{\large\bf Фр...
....00){\vector(1,0){13.00}}
\put(111.00,63.00){\vector(1,-2){13.00}}
\end{picture}](img106.png)
Рис. 21. Фрейм практического занятия
Таким образом, если в традиционной методике проведения
практического занятия большая часть учебного времени отводится на
показ образцов решения задач по теме, то в нашей методике студент
по объявленной теме и минимальным образцам решения большую часть
времени проводит за самостоятельным решением достаточного
количества задач, в том числе творческого характера. На занятие
он приходит с проблемами, ошибками и нерешенными заданиями;
преподаватель, выяснив ситуацию с домашней работой, разбирает
решения наиболее типичных задач, акцентирует внимание на ошибках,
показывает приемы творческого подхода к решению заданий.
Происходит "опережающее отражение" в формировании практических
умений в решении математических задач: получив минимальные
образцы деятельности, студент самостоятельно (или в малой группе)
определяет методы решения, сталкивается с проблемами
содержательного, субъективного, временного характера.
Самостоятельные контрольные работы (10-15 минут) создают
деятельностный фон непрерывного хранения базовой информации и
фиксируют состояние остаточной базы знаний предыдущего семестра.
Балльно-рейтинговая система оценивания стимулирует ответственное
отношение к учебной деятельности.
4. В формировании мотивационной сферы обучения математике
немаловажную роль играет проявление познавательного интереса у
студентов путем развертывания генезиса математических идей в
историческом аспекте. Работа в малых группах дает возможность, в
частности, оптимизировать число разрабатываемых исторических тем,
равно как и целостность раскрытия сущности математического
факта. Например, семестровые рефераты, отражающие историю
становления математических понятий в содержательном, прикладном,
хронологическом аспектах, создают основу для обсуждения на
коллоквиумах, научных конференциях, стимулируют развитие
творческой активности студентов, умение работать с научной и
художественной литературой.
Блок результативности обучения
Результативность обучения математике при условии диагностируемого
целеполагания и определенной системы измерителей качества
усвоения учебного материала выявляется организацией различных
средств контроля и обратной связи (теоретический, прикладной,
деятельностный,
гуманитарный, творческий модули), каждый из которых имеет свою
специфику и качественные отличия.
Система оценивания. Активное овладение методами и
технологиями усвоения знаний (в том числе на творческом уровне)
является профессиональной необходимостью для будущего учителя
математики. Поэтому процесс обучения математике в вузе
организуется таким образом, чтобы, в частности, студент,
самостоятельно работая с учебным материалом, получил образцы
(ООУД) деятельности, способствующие как усвоению знания, так и
формированию ориентировочной основы для будущей профессиональной
деятельности.
Воспользуемся балльно-рейтинговой системой оценивания для
составления графика учебного процесса.
Таблица 4
Формы учебной работы и шкала оценивания
![\begin{picture}(159.00,134.00)
\emline{68.00}{64.00}{1}{78.00}{64.00}{2}
\emline...
...13}{159.00}{55.00}{114}
\put(73.00,128.00){\makebox(0,0)[cc]{Код}}
\end{picture}](img108.png)
 Учебный элемент "Математический анализ",
I семестр
Учебный элемент "Математический анализ",
I семестр
Студенты, качественно и в срок выполняющие домашние задания,
освобождаются от текущей самостоятельной работы с максимальной
оценкой.
Для получения оценки "зачтено" по итогам работы в семестре
необходимо достичь суммы баллов не ниже 37 по всем формам учебной
деятельности. Достигшие максимальной суммы баллов (более 50)
получают особый статус экзаменационного оценивания. График
учебного процесса представлен на следующей схеме.
Таблица 5
График учебного процесса
![\begin{picture}(159.00,143.00)
\emline{3.00}{69.00}{1}{13.00}{69.00}{2}
\emline{...
...0){\makebox(0,0)[cc]{2}}
\put(155.00,128.00){\makebox(0,0)[cc]{2}}
\end{picture}](img109.png)
Рассмотрим, например, систему контроля практических умений по
теме "Интегральное исчисление". Используем фреймовое
представление знаний. Фрейм контроля состоит из следующих слотов:
Схема 11
Фрейм контроля практических умений по теме
"Интегральное исчисление"
![\begin{picture}(158.00,224.00)
\put(155.00,219.00){\makebox(0,0)[rc]{Фрейм контр...
...00}{214.00}{194}
\emline{118.00}{214.00}{195}{118.00}{224.00}{196}
\end{picture}](img110.png)
Учебно-методическое обеспечение дисциплины
Рекомендуемая литература
а) основная литература:
- 1.
- Г.М.Фихтенгольц. Курс дифференциального и интегрального
исчисления. Т. 1, 2, 3. М.: Наука, 2001.
- 2.
- А.Н.Колмогоров, С.В.Фомин. Элементы теории функций и
функционального анализа. М.: Наука, 1972.
- 3.
- Л.В.Канторович, Г.П.Акилов. Функциональный анализ. М.:
Наука, 1977.
- 4.
- А.И.Маркушевич, Л.А.Маркушевич.
Введение в теорию аналитических функций. М.: Просвещение, 1977.
- 5.
- Ю.В.Сидоров, М.В.Федорюк, М.И.Шабунин. Лекции по теории
функций комплексного переменного. М.: Наука, 1982.
- 6.
- Б.П.Демидович. Сборник задач и упражнений по
математическому анализу. М.: Наука, 1969.
- 7.
- П.И.Шмелев. Теория рядов. М.: Наука, 1978.
- 8.
- Н.С.Пискунов. Дифференциальное и интегральное
исчисление. Т. 2. М.: Наука, 1970.
б) дополнительная литература:
- 1.
- Л.Д.Кудрявцев. Математический анализ. Т. 1, 2. М.:
Высшая школа, 1973.
- 2.
- И.М.Уваренков, М.З.Маллер. Курс математического
анализа. Т. 1, 2. М.: Просвещение, 1976.
- 3.
- Л.Д.Кудрявцев, А.Д.Кутасов и др. Сборник задач по
математическому анализу. М.: Наука, 1984.
- 4.
- А.И.Маркушевич, Л.А.Маркушевич. Введение в теорию
аналитических функций. М.: Просвещение, 1977.
- 5.
- Г.Е.Шилов, Б.Л.Гуревич. Интеграл, мера и производная.
Общая теория. М.: Наука, 1967.
- 6.
- И.П.Натансон. Теория функций вещественной переменной.
М.: Наука, 1977.
- 7.
- М.А.Евграфов. Сборник задач по теории аналитических
функций. М.: Наука, 1972.
- 8.
- Б.З.Вулих. Краткий курс теории функций вещественной
переменной. М.: Наука, 1970.
Средства обеспечения освоения дисциплины
Автоматизированность и оптимальность управления контролирующей
деятельностью достигается применением педагогических
программных продуктов. Ниже приведены дидактические материалы
контроля умений с использованием компьютера.
Система контролирующих программ (4 программы по темам:
предел (Lim), производная (Dif), интеграл (Int), ряды (Sum) для
персонального компьютера
предназначена для текущего контроля базовых умений и навыков
по математическому анализу и служит целям:
а) непосредственного контроля и получения обратной связи;
б) стабилизации остаточных фреймов основных умений и
навыков;
в) систематизации и спорности изучаемого материала;
г) овладения межпредметными информационными
связями.
Данная система контроля отличается от обычного контроля
большей наглядностью и объективностью оценки, большей
самостоятельностью при выполнении заданий, большей
эффективностью оперативного контроля, возможностью вызова
правильного ответа после выполнения задания.
Каждая программа содержит банк задач трех уровней, а также
тренажер, которым студент может воспользоваться при изучении
определенного раздела математического анализа (предел функции,
дифференцирование, интегрирование, ряды). Банк задач первого
уровня содержит задачи, при решении которых
применяется не более одного из изучаемых методов и не
требуется сложных вычислений. Для решения задач второго уровня
приходится комбинировать известные методы, проводить более
сложные преобразования. Задачами третьего уровня являются
задачи повышенной трудности. Наличие банка задач трех уровней
дает возможность дифференцированного обучения студентов,
а также использования настоящего пакета программ на различных
уровнях обучения.
Банк задач каждого уровня состоит из 50 заданий 5 основных
типов, отражающих основные (базовые) умения и навыки
данного раздела математического анализа. Время выполнения
каждого из 5 заданий, получаемых случайным выбором,
фиксируется таймером с накоплением временного интервала,
влияющего на итоговую оценку. Время, отводящееся для решения
каждой задачи, погрешность при вводе числового ответа, критерии
оценки, равно как и сам банк заданий, могут быть приведены в
соответствие с требованиями преподавателя, проводящего текущий
контроль.
Целевая установка контроля:
а) информационно-межпредметные связи: знакомство с
клавиатурой, графические и функциональные возможности ЭВМ,
адекватное восприятие знаково-символических форм, отражающих
конкретное математическое содержание, мотивация обучения;
б) оперативность контроля: академическая группа из 25
студентов проходит контроль в дисплейном классе (12 мониторов)
в течение 30-40 мин. (Dif, Lim) и 100-120 мин. (Int, Sum) при
непосредственном восприятии преподавателем результатов
контроля (как количественных, так и качественных - число
решенных заданий, количество ошибок в каждом задании,
просрочка времени по каждому заданию, общее затраченное на
решение заданий время, общее количество ошибок, оценка).
Соответственно, в двух дисплейных классах время на проведение
контроля уменьшается в 2 раза;
в) система контролирующих программ позволяет создать
ассоциативно-рефлекторный фон опорных навыков и умений по
курсу математического анализа. Схема внедрения
контролирующих программ приведена ниже;
г) стабилизация остаточных фреймов - повторное включение
машинного контроля в учебный процесс стимулирует
самостоятельную подготовку студентов к изучению новых разделов
математического анализа (например, при изучении частных
производных и действий над ними требуются навыки
дифференцирования функций одного переменного, а точнее -
восстановление следов предыдущих знаний (фреймов), что
достигается повторным включением контролирующей программы
(Dif));
д) мобильность контроля - возможность изменять банк
заданий, исходя из особенностей преподавания и методических
концепций, возможность менять уровень требований к оценке
контроля, возможность менять погрешность при вводе ответа,
возможность менять временные интервалы, фиксирующие среднее
время, необходимое для выполнения отдельного задания.
Схема 12
Схема
внедрения системы контролирующих программ по математическому
анализу
![\begin{picture}(158.00,48.00)
\put(48.00,45.00){\makebox(0,0)[rc]{Раздел}}
\put(...
....00){\makebox(0,0)[cc]{+}}
\put(131.00,9.00){\makebox(0,0)[cc]{+}}
\end{picture}](img111.png)
Примечание. Программа (Int) для ввода ответа предполагает
использование микрокалькулятора.
Лабораторный практикум с использованием микрокалькуляторов
(в том числе графических) предназначен для оперативного
управления формированием и стабилизацией практических умений
конкретизации базовых понятий, теорем и процедур. Приведем
несколько примеров лабораторных работ.
1. По формуле прямоугольников найдите приближенное значение
определенного интеграла
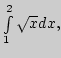 разбив
интервал интегрирования на 10 частей. Оцените погрешность,
проведите вычисления на микрокалькуляторе по программе
разбив
интервал интегрирования на 10 частей. Оцените погрешность,
проведите вычисления на микрокалькуляторе по программе
заполнив пропущенный фрагмент вычислением значений
подынтегральной функции. Напишите инструкцию к программе.
Составьте вариант программы с организацией цикла. Проведите
вычисления по этим программам для
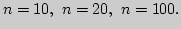 Оцените
погрешность вычислений.
Оцените
погрешность вычислений.
Указания к решению:
Пропущенный фрагмент содержит две команды
Инструкция к программе:
1. FПРГ;
2. ввести программу;
3. FABT;
4. В/О;
5.
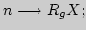
6. С/П;
7.
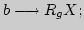
8. С/П;
9.
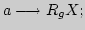
10. С/П;
11. прочитать показания индикатора;
12. перейти к п. 5, повторив вычисление для нового значения 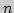 .
.
Оценим погрешность:
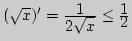 для
для ![$x\in[1;2],$](img121.png)
Результаты вычислений по программе:
Другой вариант программы с организацией цикла:
Инструкция к программе:
1. FПРГ;
2. ввести программу;
3. FABT;
4. B/O;
5.
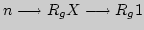 ;
;
6. С/П;
7.
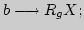
8. С/П;
9.
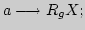
10. С/П;
11. прочитать показания индикатора;
12. перейти к п. 5.
2. По формуле трапеций найдите приближенное значение
определенного интеграла
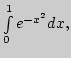 разбив
интервал интегрирования на 10 равных частей. Оцените погрешность.
Проведите вычисления на микрокалькуляторе по данной программе
разбив
интервал интегрирования на 10 равных частей. Оцените погрешность.
Проведите вычисления на микрокалькуляторе по данной программе
заполнив пропущенный фрагмент вычислением значений
подынтегральной функции. Составьте другой вариант программы без
организации цикла. Проведите вычисления по этим программам для
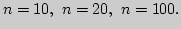 Оцените погрешность вычислений.
Оцените погрешность вычислений.
Указания к решению.
Пропущенный фрагмент программы содержит команды:
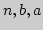 вводятся в регистр
вводятся в регистр 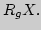
Оценим погрешность:
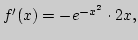
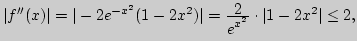
![$x\in[0;1];$](img137.png)
Результаты вычислений по программе:
Другой вариант программы без организации цикла:
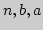 вводятся в регистр
вводятся в регистр 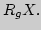
Перечень примерных контрольных вопросов и заданий
для самостоятельной работы:
1. Какие связи между параметрической, полярной и декартовой
системой координат?
2. Верна ли обратная теорема к теореме
Ферма?
3. Привести пример непрерывной функции, имеющей
бесконечное число точек несуществования производной на
конечном отрезке.
4. Дать геометрическую иллюстрацию теоремы
Коши.
5. Какие условия необходимы и достаточны для строгого
монотонного возрастания (убывания) дифференцируемой функции?
6. Как
построить непрерывную кривую, сплошь заполняющую квадрат
![$[0,1; 0,1]$](img143.png) на плоскости
на плоскости 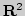 ?
?
7. Доказать бесконечную дифференцируемость в точке функции
8. Вывести формулу для

9. Указать элементарные функции, для которых константа в
формуле конечных приращений может быть конструктивно
определена.
10. Рассмотреть пример функции и ее критической
точки, когда неприменимы все 3 достаточных условия
существования экстремума.
11. Доказать теорему: для того,
чтобы непрерывная на 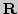 функция была выпуклой, необходимо и
достаточно, чтобы
функция была выпуклой, необходимо и
достаточно, чтобы
12. Привести примеры функций, не интегрируемых в элементарных
функциях.
13. Можно ли определить интеграл от
неограниченной функции? на неограниченном промежутке?
14. Привести пример ограниченной неинтегрируемой по Риману
функции.
15. Следует ли из интегрируемости 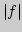 интегрируемость
интегрируемость 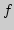 ?
?
16. Найти связь между формулой Тейлора и
формулой Лагранжа.
17.Найти связь между интегральной теоремой о среднем и дифференциальной
теоремой о среднем (формула Лагранжа).
18. Каков геометрический смысл дифференциала дуги 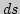 ?
?
19. Доказать теорему о необходимом и достаточном условии
интегрируемости ограниченной функции по Риману.
20. Вычислить объем эллипсоида (и, следовательно, шара), конуса,
пирамиды; площадь круга (эллипса) и задачи подобного рода,
относящиеся к школьной математике.
Примерная тематика рефератов и курсовых работ:
Рефераты (I, II семестры)
Цель: расширение когнитивного опыта в условиях
индивидуальной и совместной деятельности принятия решения: сбор
данных, выбор, активация мотивационной сферы.
Задачи: углубленное изучение и представление в форме
исторического реферата фрагмента курса математического анализа:
персоналии, вариативность подходов к проблеме, проработка деталей
информационного поля проблемы, расширение банка учебных и
творческих заданий, прикладные задачи и использование
вычислительных методов и т.п.; осуществление "обучения через
выбор"; формирование творческой активности и коммуникативных
качеств.
Формы: работа в малых группах (3-4 студента),
индивидуальные консультации.
I семестр
1. Построение графиков функций в полярной системе координат
- 1.
- Н.А.Вирченко, И.И.Ляшко, К.И.Швецов. Графики функций:
Справочник. Киев: Наук. думка, 1979.
- 2.
- Г.М.Фихтенгольц. Курс дифференциального и интегрального
исчисления. Т. 1. М.: Наука, 2001.
2. Десять исторических задач, приводящих к понятию
производной
- 1.
- А.П.Юшкевич. Концепции вычисления бесконечно малых
Ньютона и Лейбница // ИМИ. Вып. 23. 1978.
- 2.
- Д.Я. Стройк. Краткий очерк истории математики. М.: Мир,
1978.
3. Функциональные уравнения основных элементарных функций
- 1.
- Г.М.Фихтенгольц. Курс дифференциального и интегрального
исчисления. Т. 1. М.: Наука, 2001.
- 2.
- В.П.Одинец, А.И.Поволоцкий. Построение элементарных
функций. СПб.: Образование, 1995.
4. Основные элементарные функции в природе и технике
- 1.
- Н.Я.Виленкин. Функции в природе и технике. Книга для
внеклассного чтения IX-X классов. М.: Просвещение, 1978.
- 2.
- С.Г.Крейн, В.Н.Ушаков. Математический анализ
элементарных функций. М.: Наука, 1966.
- 3.
- Ф.Клейн. Элементарная математика с точки зрения высшей.
Т. 1. М.-Л., 1987.
5. Системы координат на плоскости и в пространстве
- 1.
- Л.С.Понтрягин. Метод координат. М.: Наука, 1977.
- 2.
- М.Я.Выготский. Справочник по высшей математике. М.:
Наука, 1973.
- 3.
- И.М.Гельфанд, Е.Г.Глаголева, А.А.Кириллов. Метод
координат. М., 1973.
6. Трансцендентные числа в анализе
- 1.
- В.А.Зорич. Математический анализ. Т. 1. М.: Наука,
1983.
- 2.
- Ф.Рудно. Квадратура круга. М.-Л., 1934.
- 3.
- А.О.Гельфонд. Решение уравнений в целых числах. М.-Л.,
1952.
- 4.
- А.Я.Хинчин. Три жемчужины теории чисел. М., 1979.
7. Цепные дроби и их приложения
- 1.
- А.Я. Хинчин. Цепные дроби. М.: Наука, 1978.
- 2.
- И.К.Андронов, А.К.Окунев. Арифметика рациональных
чисел. М.: Просвещение, 1971.
II семестр
Цель: освоение навыков исследовательской деятельности:
включенность в математическую проблему, генезис идей и
вариативность подходов, сбор данных и перенос знаний, выделение
базовых, значимых компонентов проблемы, готовность к принятию
нестандартных решений.
Задачи: инновационное самостоятельное решение конкретных
математических задач и проблем: новые банки задач и примеров,
новые доказательства известных теорем, поиск новых процедур и
алгоритмов, интегративные подходы и структурирование
математической информации, визуализация математических объектов и
т.п.; осуществление совместной творческой деятельности, обмен
информацией и распределением ролей в функционировании малых
групп, развитие речевой культуры и коммуникативных качеств,
наращивание интеллектуального опыта.
Формы: работа в малых группах (3-4 студента),
индивидуальные консультации, публичные защиты
рефератов-исследований.
1. Контрпримеры в теории множеств
- 1.
- Б.Гелбаум, Дж. Олмстед. Контрпримеры в анализе. М.:
Мир, 1967.
- 2.
- К.Куратовский. Теория множеств. М.: Мир, 1970.
- 3.
- П.Коэн. Теория множеств и континуум-гипотеза. М.: Мир,
1969.
2. Методы построения графиков функций в параметрических
координатах
- 1.
- Н.А.Вирченко, И.И.Ляшко, К.И.Швецов. Графики функций:
Справочник. Киев: Наук. думка, 1979.
- 2.
- Б.П.Демидович. Сборник задач и упражнений по
математическому анализу. М.: Наука, 1969.
3. Контрпримеры в теории функциональных рядов
- 1.
- Б.Гелбаум, Дж. Олмстед. Контрпримеры в анализе. М.:
Мир, 1967.
- 2.
- П.И.Шмелев. Теория рядов. М.: Наука, 1978.
- 3.
- Г.М.Фихтенгольц. Курс дифференциального и интегрального
исчисления. Т. 2. М.: Наука, 2001.
4. Особые решения дифференциальных уравнений первого
порядка
- 1.
- Н.М.Матвеев. Методы интегрирования обыкновенных
дифференциальных уравнений. М.: Высшая школа, 1967.
- 2.
- Н.С.Пискунов. Дифференциальное и интегральное
исчисление. Т. 2. М.: Наука, 1970.
5. Ортогональные системы функций в анализе
- 1.
- Г.Алексич. Проблемы сходимости ортогональных рядов. М.:
Иностранная литература, 1963.
- 2.
- А.Н.Колмогоров, С.В.Фомин. Элементы теории функций и
функционального анализа. М.: Наука, 1972.
Спирали фундирования (III-IV семестры)
Цель: построение дидактического фрейма спирали фундирования
базового учебного элемента (понятия, теоремы, алгоритма,
процедуры).
Задачи: освоение структуры и состава дидактического фрейма
учебного элемента, мотивационное оснащение блоков спирали
фундирования учебного элемента, выделение существенной связи
теоретического (эмпирического) обобщения, структурный анализ сфер
деятельности (вербальной, знаково-символической, графической,
конкретно-деятельностной) с блоками спирали фундирования.
Формы: работа в малых группах (3-4 студента),
индивидуальные консультации, обмен информацией между малыми
группами, анализ и публичная оценка.
Лабораторный практикум
| №
п/п |
№
раздела учеб. предм. |
Наименование лабораторной
работы |
| 1 |
1 |
1. Компьютерный контроль 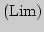 по теме "Предел
функции" (2 часа) по теме "Предел
функции" (2 часа)
2. Нахождение корней трансцендентных уравнений (графический
калькулятор) (2 часа) |
| 2 |
2 |
1. Компьютерный контроль 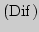 по теме "Производная"
(2 часа) по теме "Производная"
(2 часа)
2. Нахождение
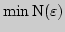 для числовой последовательности для числовой последовательности
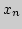 (педагогический программный продукт) (2 часа) (педагогический программный продукт) (2 часа)
3. Нахождение корней многочлена методом хорд (графический
калькулятор) (2 часа) |
| 3 |
3 |
1. Компьютерный контроль 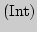 по теме "Интеграл" (2
часа) по теме "Интеграл" (2
часа)
2. Нахождение значений определенного интеграла методом трапеций
(графический калькулятор) (2 часа) |
| 4 |
4 |
1. Градиентные методы нахождения экстремума (2 часа)
2. Метод последовательных приближений в 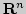 (2 часа) (2 часа)
3. Численное интегрирование в 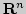 (2 часа) (2 часа) |
| 5 |
5 |
1. Компьютерный контроль 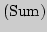 по теме "Ряды" (2 часа) по теме "Ряды" (2 часа)
2. Распознавание типа дифференциального уравнения (педагогический
программный продукт) (1 час)
3. Численное решение дифференциального уравнения 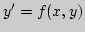 методом Рунге-Кутта (графический калькулятор) (2 часа)
методом Рунге-Кутта (графический калькулятор) (2 часа) |
| 6 |
6 |
1. Решение уравнения Фредгольма (2 часа)
2. Геометрия конформных отображений (2 часа) |
Курсовая работа (V-VI семестры)
Цель: расширение научного кругозора, формирование навыков
самостоятельного научного исследования, решение конкретных задач
и проблем математики.
Задачи: построение альтернативных конструкций доказательств
известных теорем, решение проблем визуализации сложных
математических объектов, теоретический и практический анализ
особенностей и частных проявлений математических знаний.
Формы: выполнение индивидуально или в паре (1-2 человека),
индивидуальные консультации с научным руководителем,
публичная защита на кафедре.
Цепочки задач учебно- и научно-исследовательского характера
Активному овладению курсом математического анализа, развитию
творческой самостоятельности студентов, более глубокому
проникновению в качественный анализ основных понятий, методов и
теорем математического анализа могут служить приводимые ниже
цепочки задач учебно- и научно-исследовательского характера,
имеющие непосредственный выход на серьезное математическое
исследование. Решение этих задач требует самостоятельных
математических рассуждений, ознакомления и проработки
научно-методической литературы, умения обрабатывать научную
информацию, делать самостоятельные выводы. Каждый цикл
представляет собой логическую цепочку заданий, связанную единой
опорной идеей, с постепенным накоплением информации о реализации
этой идеи. Завершающие задачи цикла могут стать основой курсовых
и дипломных работ.
Метод последовательных приближений
1. Доказать, что последовательность, задаваемая рекуррентным
соотношением: 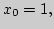
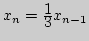 , сходится.
, сходится.
2. Найти пределы последовательностей:
а)
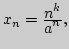
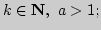
б)
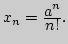
3. Пусть 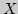 -
- 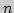 - мерное пространство, в котором расстояние
определяется по формуле
- мерное пространство, в котором расстояние
определяется по формуле
где
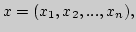
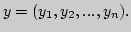
Пусть отображение
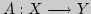 задается системой линейных
уравнений
задается системой линейных
уравнений
При каких условиях отображение 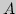 будет сжимающим, т.е.
будет сжимающим, т.е.
где
4. При каких значениях параметра 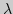 оператор
оператор
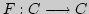 ,
задаваемый формулой
,
задаваемый формулой
будет сжимающим? Методом последовательных приближений найти
решение уравнения 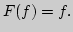
5. Составить блок-схему, определить метод вычислений и программу
на алгоритмическом языке для задачи 4. Обеспечить
эффективную оценку погрешности и практически обеспечить заданную
точность.
Литература
- 1.
- Бобков В.В., Городецкий Л.М. Избранные численные методы
решения на ЭВМ инженерных и научных задач. Минск: Вышейша школа, 1985.
- 2.
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и
функционального анализа. М.: Наука, 1972.
- 3.
- Фихтенгольц Г.М. Курс дифференциального и интегрального
исчисления. Т. 1. М.: Наука, 1969.
Компактность
1. Будут ли следующие множества ограничены:
2. Будут ли семейства функций равномерно ограниченными:
3. Будут ли следующие функции непрерывны, на каких множествах:
4. Исследовать функции на равномерную непрерывность. Результат
обосновать на языке
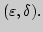
5. Пусть
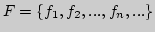 - некоторое семейство
функций. Будет ли
- некоторое семейство
функций. Будет ли 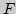 равностепенно непрерывным, если:
равностепенно непрерывным, если:
а) 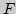 состоит из конечного числа равномерно непрерывных функций;
состоит из конечного числа равномерно непрерывных функций;
б)
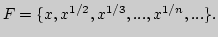
6. С помощью теоремы Арцела определить, являются ли следующие
множества функций предкомпактными в равномерной метрике (по
 ):
):
а)
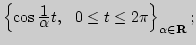
б)
![$\left\{e^{\alpha t}, 0\le t\le1\right\}_{\alpha \in[0,1]}.$](img187.png)
Литература
- 1.
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и
функционального анализа. М.: Наука, 1972.
- 2.
- Макаров И.П. Дополнительные главы математического
анализа. М.: Просвещение, 1966.
Последовательность
1. Пусть 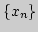 ограниченная последовательность. Следует ли
отсюда ее сходимость?
ограниченная последовательность. Следует ли
отсюда ее сходимость?
2. Пусть дано бесконечное число последовательностей:
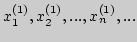 |
- I
последовательность, |
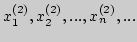 |
- II
последовательность, |
| ................ |
|
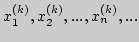 |
- 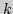 последовательность.
последовательность. |
Известно, что для любого 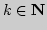 последовательность
последовательность
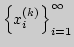 сходится к нулю и для
любого
сходится к нулю и для
любого 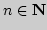 последовательность
последовательность
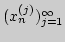 сходится к нулю. Что можно сказать о сходимости "диагональной"
последовательности
сходится к нулю. Что можно сказать о сходимости "диагональной"
последовательности
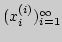 ?
?
3. Пусть
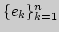 - какой-нибудь базис пространства
- какой-нибудь базис пространства
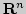 , тогда любой элемент последовательности
, тогда любой элемент последовательности
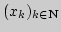 может быть представлен в виде:
может быть представлен в виде:
Доказать: для того, чтобы последовательность
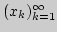 сходилась к вектору
сходилась к вектору
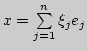 , необходимо и
достаточно, чтобы
, необходимо и
достаточно, чтобы
4. Доказать: если все сходящиеся подпоследовательности некоторой
ограниченной последовательности 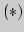 имеют один и тот же предел,
то и сама последовательность сходится к этому пределу.
имеют один и тот же предел,
то и сама последовательность сходится к этому пределу.
5. Пусть 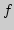 непрерывная функция на отрезке
непрерывная функция на отрезке ![$[-\pi,\pi]$](img205.png) и
и
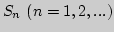 частичные суммы ряда Фурье функции
частичные суммы ряда Фурье функции 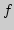 . Пусть далее
. Пусть далее
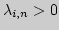 и
и
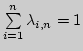
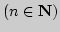 ,
,
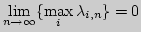 . Доказать, что
последовательность функций
. Доказать, что
последовательность функций
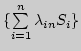 сходится равномерно к функции
сходится равномерно к функции 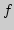 на отрезке
на отрезке ![$[-\pi,\pi].$](img212.png)
Литература
- 1.
- Фихтенгольц Г.М. Курс дифференциального и интегрального
исчисления. Т. III. М.: Наука, 1969.
Выпуклость
1. Описать все замкнутые, выпуклые множества на прямой.
2. Пусть 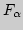 - произвольное семейство замкнутых, выпуклых
множеств на прямой. Доказать: если любые два множества семейства
- произвольное семейство замкнутых, выпуклых
множеств на прямой. Доказать: если любые два множества семейства
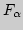 пересекаются по непустому множеству, то все множества
имеют общую точку.
пересекаются по непустому множеству, то все множества
имеют общую точку.
3. Пусть 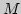 - замкнутое выпуклое множество на плоскости. Если
- замкнутое выпуклое множество на плоскости. Если
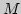 - ограниченное множество, всегда ли проекция
- ограниченное множество, всегда ли проекция 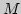 на одну из
координатных осей является выпуклым замкнутым множеством?
Провести доказательство. Те же вопросы для неограниченного
множества
на одну из
координатных осей является выпуклым замкнутым множеством?
Провести доказательство. Те же вопросы для неограниченного
множества 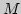 .
.
4. Пусть 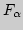 - произвольное семейство замкнутых,
ограниченных, выпуклых множеств на плоскости. Используя задачу 2,
показать, что если любые четыре множества из
- произвольное семейство замкнутых,
ограниченных, выпуклых множеств на плоскости. Используя задачу 2,
показать, что если любые четыре множества из 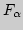 имеют общую
точку, то и все множества имеют общую точку.
имеют общую
точку, то и все множества имеют общую точку.
Указание. Рассмотреть проекции на одну из координатных осей
попарных пересечений множеств из 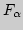 .
.
5. Если пересечение любых трех из 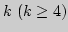 ограниченных
замкнутых выпуклых множеств на плоскости не пусто, то и
пересечение всех
ограниченных
замкнутых выпуклых множеств на плоскости не пусто, то и
пересечение всех 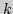 множеств также не пусто (теорема Хелли).
множеств также не пусто (теорема Хелли).
6. Доказать теорему Каратеодори: всякое выпуклое подмножество
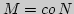 из
из 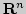 может быть представлено как выпуклая
оболочка не более чем
может быть представлено как выпуклая
оболочка не более чем 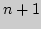 точек из
точек из 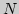 .
.
Литература
- 1.
- Рокафеллар Р. Выпуклый анализ. М.: Мир, 1976.
Приближение
1. Найти точные нижние и верхние грани следующих множеств:
Пусть 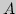 - некоторое подмножество метрического пространства
- некоторое подмножество метрического пространства
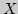 . Через
. Через 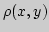 будем обозначать расстояние между
элементами
будем обозначать расстояние между
элементами 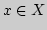 и
и 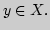 Наилучшим приближением элемента
Наилучшим приближением элемента
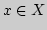 элементами множества
элементами множества 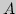 называется число
называется число
Элемент 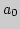 , на котором достигается точная нижняя грань,
называется элементом наилучшего приближения.
, на котором достигается точная нижняя грань,
называется элементом наилучшего приближения.
Геометрически наилучшее приближение элемента 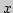 есть расстояние
от
есть расстояние
от 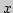 до множества
до множества 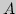 , а элемент наилучшего приближения -
точка
, а элемент наилучшего приближения -
точка 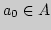 , ближайшая к
, ближайшая к 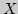 .
.
2. Пусть 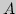 - множество рациональных чисел из
- множество рациональных чисел из ![$[0,1]$](img227.png) ,
, 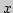 -
иррациональное число, принадлежащее этому отрезку. Найти
наилучшее приближение
-
иррациональное число, принадлежащее этому отрезку. Найти
наилучшее приближение 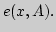
3. Пусть
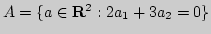 - прямая на плоскости.
Найти наилучшее приближение для точки
- прямая на плоскости.
Найти наилучшее приближение для точки 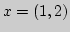 элементами
множества
элементами
множества 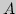 в пространстве
в пространстве
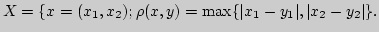 Найти
элемент наилучшего приближения; будет ли он единственным?
Найти
элемент наилучшего приближения; будет ли он единственным?
4. Найти 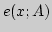 и элемент наилучшего приближения, используя три
способа измерения расстояний на плоскости:
и элемент наилучшего приближения, используя три
способа измерения расстояний на плоскости:
а)
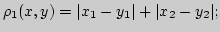
б)
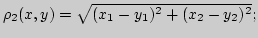
в)
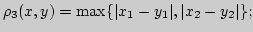
если 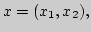
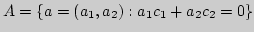 , здесь
, здесь
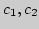 - произвольные действительные числа.
- произвольные действительные числа.
Литература
- 1.
- Ахиезер Н.И. Лекции по теории аппроксимации. М.: Наука,
1965.
- 2.
- Канторович Л.В., Акилов Г.П. Функциональный анализ. М.:
Наука, 1977.
Числовые ряды и вероятность
1. Докажите, что
а)
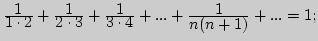
б)
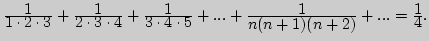
2. Найдите сумму ряда:
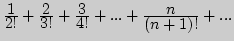
3. а) Классический, вероятностный и геометрический способы
суммирования геометрической прогрессии.
б) При последовательном вычислении с возвратом из полного набора
домино первый поставил на нечетную сумму, а второй на четную. В
каком соотношении находятся их шансы на победу?
4. Покажите геометрическим и вероятностным способами, что
а)
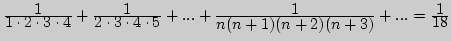 ;
;
б)
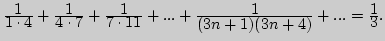
5. Найдите вероятностным и геометрическим способами суммы
следующих рядов:
а)
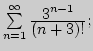
б)
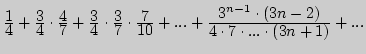
Литература
- 1.
- Афанасьев В.В.
Формирование творческой активности студентов в процессе
решения математических задач. Ярославль: Изд-во ЯГПУ, 1996.
6.4. Примерный перечень вопросов к экзамену
(интегративные учебные элементы).
1. Мощность множества. Шкала мощностей (упорядочение,
неограниченность сверху, линейность). Счетные множества.
Несчетность континуума.
Построение шкалы мощностей с помощью факторизации по отношению
эквивалентности. Теорема Кантора-Бернштейна. Несчетность
интервала и всей прямой. Теорема Кантора о высших мощностях.
Счетность множества рациональных чисел. Мощности множеств 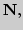
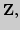
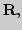
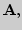
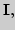
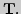
2. Аксиоматическое построение множества действительных чисел. Три
теории действительных чисел.
Основные группы аксиом: сложение, умножение, порядок, связи,
аксиома непрерывности. Лемма Кантора о вложенных отрезках.
Натуральные числа, метод математической индукции. Подклассы 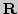 (натуральные
(натуральные 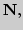 целые
целые 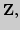 рациональные
рациональные 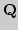 ,
иррациональные
,
иррациональные 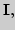 алгебраические
алгебраические  , трансцендентные
числа), их мощности. Теории действительных чисел Г.Кантора,
Р.Дедекинда, К.Вейерштрасса (исторический анализ, различие и
взаимосвязи).
, трансцендентные
числа), их мощности. Теории действительных чисел Г.Кантора,
Р.Дедекинда, К.Вейерштрасса (исторический анализ, различие и
взаимосвязи).
3. Принцип Архимеда. Позиционные системы счисления. Двоичная
система счисления и ЭВМ.
Формулировка и геометрическая трактовка принципа Архимеда.
Приложение принципа Архимеда. Плотность множества 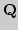 в
в 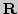 .
Рациональное приближение действительных чисел. Позиционная
система счисления, взаимный переход из одной системы счисления в
другую. Запись информации в память ЭВМ, понятие бита и байта
информации.
.
Рациональное приближение действительных чисел. Позиционная
система счисления, взаимный переход из одной системы счисления в
другую. Запись информации в память ЭВМ, понятие бита и байта
информации.
4. Отображения множеств, типы и классификация. Операции над
отображениями
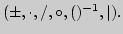
Отображение множеств (эволюция понятий, современная трактовка
понятия функции). Типы отображений: инъекция, сюръекция, биекция.
Классификация отображений:
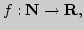
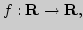
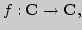
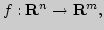
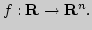 Операции
над отображениями: арифметические, композиции, обращение,
сужение, продолжение. Построить непрерывное продолжение
показательной функции
Операции
над отображениями: арифметические, композиции, обращение,
сужение, продолжение. Построить непрерывное продолжение
показательной функции 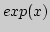 с
с 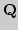 на
на 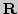 (провести
доказательство непрерывности и теоремы сложения).
(провести
доказательство непрерывности и теоремы сложения).
5. Основные элементарные функции, множество элементарных функций.
Классификация элементарных функций. Неэлементарные функции.
Основные элементарные функции: постоянная, степенная,
показательная, логарифмическая, тригонометрические, обратные
тригонометрические; графики и основные свойства. Системы
координат на плоскости и в пространстве: декартова, полярная,
параметрическая, задание элементарных функций, взаимопереход
различных систем координат. Мера угла, построение
тригонометрических функций (вычисление площади сектора или длины
дуги). Многочлены, рациональные, иррациональные, алгебраические,
трансцендентные функции; примеры. Неэлементарные функции;
примеры.
6. Элементарные функции в комплексной плоскости.
Основные элементарные функции в комплексной области:
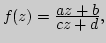
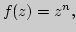
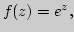
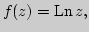
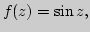 различные подходы к определению, идея
аналитического продолжения, свойства. Доказательство формулы
различные подходы к определению, идея
аналитического продолжения, свойства. Доказательство формулы
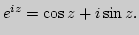
7. Аксиоматическое представление основных элементарных функций.
Формула и ряд Тейлора.
Линейное, квадратичное, полиномиальное приближение основных
элементарных функций. Формулы Лагранжа и Тейлора, ряд Тейлора.
Остаточные члены в форме Пеано и Лагранжа. Разложение основных
элементарных функций: 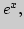
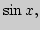

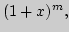
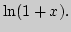 Единственность разложения в ряд Тейлора.
Единственность разложения в ряд Тейлора.
8. Предел функции в точке 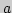 . Пространство
. Пространство 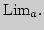 Односторонние и бесконечные пределы. Признаки существования
предела. Замечательные пределы.
Односторонние и бесконечные пределы. Признаки существования
предела. Замечательные пределы.
Предел функции в точке (окрестностное определение),
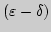 -язык, язык последовательностей (по Гейне).
Эквивалентность
-язык, язык последовательностей (по Гейне).
Эквивалентность
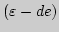 -языка и языка Гейне. Предел
последовательности. Алгебраическая структура
-языка и языка Гейне. Предел
последовательности. Алгебраическая структура 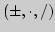 и
структура отношения порядка
и
структура отношения порядка 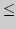 на множестве
на множестве 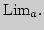 Замечательные пределы, число
Замечательные пределы, число 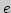 . Признаки существования предела.
. Признаки существования предела.
9. Топология числовой прямой. Окрестность точки в  Строение открытых и замкнутых множеств в
Строение открытых и замкнутых множеств в 
Окрестность точки в 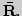 Отделимость окрестностей.
Классификация точек: предельная, внутренняя и граничные точки
множества. Строение открытых и замкнутых множеств в
Отделимость окрестностей.
Классификация точек: предельная, внутренняя и граничные точки
множества. Строение открытых и замкнутых множеств в  Методы
решения неравенств, содержащих модуль.
Методы
решения неравенств, содержащих модуль.
10. Метрические пространства 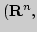
![$C_{[a;b]},$](img282.png)
![$C^1_{]a;b[},$](img283.png)
![$c^\infty_{]a;b[}$](img284.png) ). Сходимость в метрическом
пространстве. Полные метрические пространства. Метод
последовательных приближений.
). Сходимость в метрическом
пространстве. Полные метрические пространства. Метод
последовательных приближений.
Метрические пространства; примеры. Неравенство
Коши-Буняковского.
Покоординатная сходимость, равномерная сходимость, интегральная
сходимость; примеры. Теорема Банаха. Сжимающие операторы в 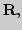 приложение к приближенному решению уравнения
приложение к приближенному решению уравнения 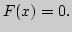 Вычисление
Вычисление
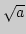 методом последовательных приближений.
методом последовательных приближений.
11. Непрерывность функции в точке метрического пространства.
Алгебраическая структура и полнота пространства ![$C_{[a;b]}.$](img287.png)
Непрерывность функции в метрическом пространстве
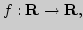
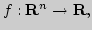
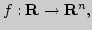
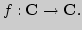 Непрерывность основных элементарных функций. Алгебраическая
структура
Непрерывность основных элементарных функций. Алгебраическая
структура 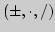 и полнота пространства
и полнота пространства ![$C+{[a;b]}$](img291.png) в
равномерной метрике. Использование непрерывности при нахождении
предела функции.
в
равномерной метрике. Использование непрерывности при нахождении
предела функции.
12. Свойства функций, непрерывных на отрезке. Метод
Больцано.
Теоремы Больцано-Коши и Вейерштрасса, непрерывность композиции и
обращение (доказательство теоремы Больцано-Коши методом
Больцано). Доказательство включения
![$C^1_{]a;b[}\subset
C_{]a;b[}.$](img292.png) Примеры непрерывных, но не дифференцируемых функций с
доказательством.
Примеры непрерывных, но не дифференцируемых функций с
доказательством.
13.Задачи, приводящие к понятию производной. Дифференциал
функции. Пространство ![$C^1_{]a;b[}$](img293.png) .
.
Задачи о касательной, о плотности, о скорости с обоснованием.
Исторические подходы к введению производной (Ньютон, Лейбниц).
Дифференциал функции как средство приближенного выражения
приращения функции, его геометрический и механический смысл.
Производные основных элементарных функций, использование цепного
правила дифференцирования и производной обратной функции.
Алгебраическая структура пространства ![$C^1_{]a;b[}.$](img294.png)
14. Развитие понятия производной:
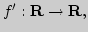
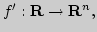
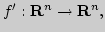
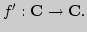 Условие
дифференцируемости функции.
Условие
дифференцируемости функции.
Развитие понятия производной (число, вектор-функция, градиент,
оператор), определения и взаимосвязи. Условия Коши-Римана
дифференцируемости функции комплексного переменного. Примеры
производной на каждый случай. Геометрический и физический смысл
производных.
15. Исследование функции на экстремум. Нахождение
наибольшего и наименьшего значения функции, непрерывно
дифференцируемой на отрезке.
Локальный и глобальный экстремумы функции; определение и примеры
в 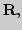
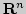
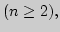
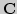 ). Необходимое (теорема Ферма) и
3 достаточных условия существования экстремума в
). Необходимое (теорема Ферма) и
3 достаточных условия существования экстремума в  Стационарные и критические точки функции; примеры в
Стационарные и критические точки функции; примеры в 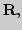
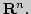 Метод наискорейшего спуска для
Метод наискорейшего спуска для 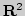 (алгоритм).
Нахождение
(алгоритм).
Нахождение 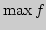 и
и 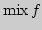 (
(
![$f\in C^1_{]a;b[}).$](img303.png)
16. Интегрирование как обратная операция к
дифференцированию. Формула Ньютона-Лейбница. Техника
неопределенного интегрирования.
Задача восстановления 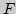 из выражения
из выражения
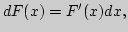 обращение дифференциального оператора
обращение дифференциального оператора
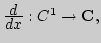 линейность и структура ядра
линейность и структура ядра 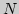 оператора
оператора
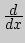 .
Существование
.
Существование
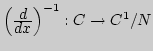 ,
линейность и обратимость
,
линейность и обратимость
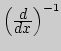 ,
обозначение
,
обозначение
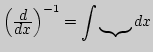 ,
геометрический и физический смысл первообразной, основная теорема
интегрального исчисления. Техника неопределенного интегрирования
(по частям, подстановка, интегрирование рациональных функций);
примеры.
,
геометрический и физический смысл первообразной, основная теорема
интегрального исчисления. Техника неопределенного интегрирования
(по частям, подстановка, интегрирование рациональных функций);
примеры.
17. Задачи, приводящие к понятию интеграла. Интеграл Римана.
Класс интегрируемых функций.
Метод бесконечно малых. Задачи о площади плоской фигуры, о длине
дуги, об объеме тела, о работе силового поля, о массе линейного
стержня. Интеграл Римана. Класс 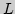 интегрируемых функций
(алгебраическая структура, отношение порядка), аддитивность и
монотонность интеграла Римана; примеры. Пример неинтегрируемой по
Риману функции. Методика применения определенного интеграла к
решению практических задач.
интегрируемых функций
(алгебраическая структура, отношение порядка), аддитивность и
монотонность интеграла Римана; примеры. Пример неинтегрируемой по
Риману функции. Методика применения определенного интеграла к
решению практических задач.
18. Равномерная сходимость функционального ряда. Методы
разложения элементарных функций. Определение 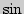 и
и 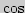 .
.
Равномерная сходимость - сходимость в метрике ![$C_{[a;b]}.$](img287.png) Примеры равномерно и неравномерно сходящихся рядов. Почленное
дифференцирование и интегрирование функционального ряда. Методы
разложения элементарных функций в функциональный ряд
(геометрическая прогрессия,
Примеры равномерно и неравномерно сходящихся рядов. Почленное
дифференцирование и интегрирование функционального ряда. Методы
разложения элементарных функций в функциональный ряд
(геометрическая прогрессия,
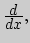
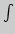 ).
).
Числа 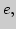
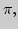
 (вычисление и оценка погрешности).
Определение
(вычисление и оценка погрешности).
Определение  и
и  посредством функционального ряда.
посредством функционального ряда.
19.Линейные дифференциальные уравнения 2-го порядка с
постоянными коэффициентами. Применение к колебательным процессам.
Линейные дифференциальные уравнения 2-го порядка (однородные и
неоднородные). Структура общего решения. Задача Коши и
единственность ее решения. Геометрическое и физическое
истолкование начальных условий. Нахождение общего решения
уравнения 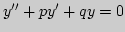 . Исследование решения дифференциального
уравнения колебательного процесса (свободные и вынужденные
колебания, резонанс).
. Исследование решения дифференциального
уравнения колебательного процесса (свободные и вынужденные
колебания, резонанс).
20. Обыкновенные дифференциальные уравнения. Теорема Пикара.
Дифференциальные уравнения основных элементарных функций.
Задачи, приводящие к понятию дифференциального уравнения.
Постановка задачи Коши, геометрический и физический смысл.
Теорема Пикара для уравнения 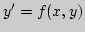 методом последовательных
приближений. Функциональные и дифференциальные уравнения основных
элементарных функций и их решения методом функциональных рядов.
методом последовательных
приближений. Функциональные и дифференциальные уравнения основных
элементарных функций и их решения методом функциональных рядов.
Далее: Дидактический модуль "Введение в
Вверх: Теоретические основы наглядного моделирования
Назад: §3. Педагогический процесс наглядно-модельного
ЯГПУ, Центр информационных технологий обучения
25.04.2008
![]() алгебраические,
алгебраические,
![]() порядковые,
порядковые,
![]() вероятностные,
вероятностные,
![]() геометрические (кривые, поверхности, графы),
геометрические (кривые, поверхности, графы),
![]() функциональные (мера, производная, интеграл, ряд)
функциональные (мера, производная, интеграл, ряд)![\begin{picture}(160.00,207.00)
\put(80.00,204.00){\makebox(0,0)[cc]{Введение}}
\...
....00}{188.00}{306}
\emline{72.00}{174.00}{307}{102.00}{174.00}{308}
\end{picture}](img83.png)
![\begin{picture}(161.00,130.00)
\put(78.00,125.00){\makebox(0,0)[cc]{Исходное сос...
...0){\vector(4,-1){19.00}}
\put(112.00,72.00){\vector(-4,-1){19.00}}
\end{picture}](img85.png)
![\begin{picture}(162.00,100.00)
\put(15.00,97.00){\makebox(0,0)[cc]{\bf Педагогич...
...00){\vector(0,-1){13.00}}
\put(144.00,41.00){\vector(0,-1){13.00}}
\end{picture}](img86.png)
![\begin{picture}(124.00,30.00)
\put(25.00,20.00){\framebox (9.00,10.00)[cc]{$\dow...
...){\makebox(0,0)[cc]{$X$}}
\put(124.00,20.00){\makebox(0,0)[cc]{,}}
\end{picture}](img87.png)
![\begin{picture}(159.00,230.00)
\put(80.00,227.00){\makebox(0,0)[cc]{ОСНОВНЫЕ}}
\...
...}{120.00}{19.00}{32}
\emline{114.00}{14.00}{33}{119.00}{19.00}{34}
\end{picture}](img92.png)
![\begin{picture}(159.00,131.00)
\put(80.00,128.00){\makebox(0,0)[cc]{ОСНОВНЫЕ}}
\...
...40.64}{14.62}{22}
\put(137.00,29.00){\makebox(0,0)[cc]{$\Omega $}}
\end{picture}](img93.png)
![\begin{picture}(120.00,27.00)
\put(20.00,18.00){\makebox(0,0)[cc]{+}}
\emline{17...
...18.00){\circle{5.66}}
\put(120.00,27.00){\makebox(0,0)[cc]{(OTK)}}
\end{picture}](img94.png)
![\begin{picture}(140.00,41.00)
\put(31.00,37.00){\makebox(0,0)[cc]{Опорная таблиц...
...7.00){\vector(2,-1){30.00}}
\put(70.00,22.00){\vector(0,-1){9.00}}
\end{picture}](img95.png)
![\begin{picture}(159.00,122.00)
\put(133.00,117.00){\makebox(0,0)[rc]{Фрейм}}
\pu...
...43.00}{60.00}{192}
\emline{143.00}{66.00}{193}{157.00}{66.00}{194}
\end{picture}](img96.png)
![\begin{picture}(114.00,65.00)
\put(80.00,62.00){\makebox(0,0)[cc]{Схема динамики...
...00}{6.00}{14}
\put(48.00,3.00){\dashbox{4.00}(64.00,51.00)[cc]{ }}
\end{picture}](img97.png)
![\begin{picture}(158.00,76.00)
\put(3.00,73.00){\makebox(0,0)[lc]{1.}}
\put(18.00...
...makebox(0,0)[lc]{- компонент школьных знаний(профессиональных).}}
\end{picture}](img98.png)
![\begin{picture}(142.00,95.00)
\put(80.00,92.00){\makebox(0,0)[cc]{ЗУНМА}}
\put(8...
...0}{103}{67.00}{44.00}{104}
\put(64.00,41.00){\makebox(0,0)[rc]{Г}}
\end{picture}](img99.png)

![\begin{picture}(147.00,44.00)
\put(20.00,44.00){\makebox(0,0)[cc]{АУП}}
\put(20....
...0,0)[cc]{ДМ$_i$}}
\put(130.00,3.00){\makebox(0,0)[cc]{ДМ$_{i+1}$}}
\end{picture}](img101.png)
![\begin{picture}(160.00,84.00)
\put(108.00,80.00){\makebox(0,0)[rc]{\small Учебны...
...,23.00){\vector(1,3){9.00}}
\put(133.00,38.00){\vector(1,2){7.00}}
\end{picture}](img102.png)
![\begin{picture}(157.00,102.00)
\put(154.00,98.00){\makebox(0,0)[rc]{Фрейм}}
\put...
...{157.00}{102.00}{54}
\emline{157.00}{102.00}{55}{1.00}{102.00}{56}
\end{picture}](img103.png)
![\begin{picture}(158.00,121.00)
\put(80.00,116.00){\makebox(0,0)[cc]{$f(x_0+h)=f(...
...{85}{80.00}{52.00}{86}
\emline{24.00}{40.00}{87}{24.00}{39.00}{88}
\end{picture}](img104.png)
![\begin{picture}(155.00,62.00)
\put(5.00,55.00){\framebox (40.00,7.00)[cc]{Истори...
...{45}{60.00}{18.00}{46}
\emline{80.00}{25.00}{47}{80.00}{18.00}{48}
\end{picture}](img105.png)
![\begin{picture}(158.00,120.00)
\put(86.00,115.00){\makebox(0,0)[lc]{\large\bf Фр...
....00){\vector(1,0){13.00}}
\put(111.00,63.00){\vector(1,-2){13.00}}
\end{picture}](img106.png)
![\begin{picture}(159.00,134.00)
\emline{68.00}{64.00}{1}{78.00}{64.00}{2}
\emline...
...13}{159.00}{55.00}{114}
\put(73.00,128.00){\makebox(0,0)[cc]{Код}}
\end{picture}](img108.png)
![\begin{picture}(159.00,143.00)
\emline{3.00}{69.00}{1}{13.00}{69.00}{2}
\emline{...
...0){\makebox(0,0)[cc]{2}}
\put(155.00,128.00){\makebox(0,0)[cc]{2}}
\end{picture}](img109.png)
![\begin{picture}(158.00,224.00)
\put(155.00,219.00){\makebox(0,0)[rc]{Фрейм контр...
...00}{214.00}{194}
\emline{118.00}{214.00}{195}{118.00}{224.00}{196}
\end{picture}](img110.png)
![\begin{picture}(158.00,48.00)
\put(48.00,45.00){\makebox(0,0)[rc]{Раздел}}
\put(...
....00){\makebox(0,0)[cc]{+}}
\put(131.00,9.00){\makebox(0,0)[cc]{+}}
\end{picture}](img111.png)
 разбив
интервал интегрирования на 10 частей. Оцените погрешность,
проведите вычисления на микрокалькуляторе по программе
разбив
интервал интегрирования на 10 частей. Оцените погрешность,
проведите вычисления на микрокалькуляторе по программе
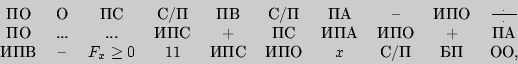
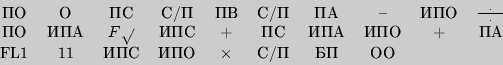
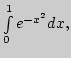 разбив
интервал интегрирования на 10 равных частей. Оцените погрешность.
Проведите вычисления на микрокалькуляторе по данной программе
разбив
интервал интегрирования на 10 равных частей. Оцените погрешность.
Проведите вычисления на микрокалькуляторе по данной программе

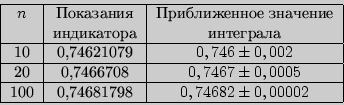

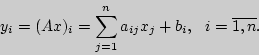
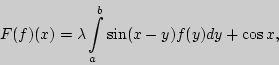
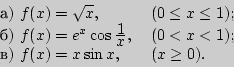

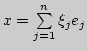 , необходимо и
достаточно, чтобы
, необходимо и
достаточно, чтобы
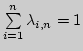
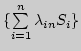 сходится равномерно к функции
сходится равномерно к функции 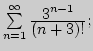
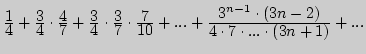
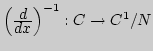 ,
линейность и обратимость
,
линейность и обратимость
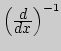 ,
обозначение
,
обозначение
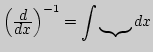 ,
геометрический и физический смысл первообразной, основная теорема
интегрального исчисления. Техника неопределенного интегрирования
(по частям, подстановка, интегрирование рациональных функций);
примеры.
,
геометрический и физический смысл первообразной, основная теорема
интегрального исчисления. Техника неопределенного интегрирования
(по частям, подстановка, интегрирование рациональных функций);
примеры.