Определение 1. Пусть функция ![]() определена в некоторой окрестности
определена в некоторой окрестности
![]() точки
точки ![]() . Придавая независимой переменной приращение
. Придавая независимой переменной приращение ![]() х,
невыводящее за пределы окрестности, получим новое значение
х,
невыводящее за пределы окрестности, получим новое значение
![]() +
+![]() х, также принадлежащее окрестности
х, также принадлежащее окрестности ![]() . Тогда значение функции
. Тогда значение функции ![]() заменится новым значением
заменится новым значением
![]() , то есть
получит приращение
, то есть
получит приращение
![]() у =
у = ![]() f(x
f(x
![]() +
+![]() х) - f(x
х) - f(x![]() .
.
Если существует предел отношения приращении функции ![]() у к вызвавшему его
приращению независимой переменной
у к вызвавшему его
приращению независимой переменной ![]() х при стремлении
х при стремлении ![]() х к 0, т.е.
х к 0, т.е.
![]() , то
он называется производной функции
, то
он называется производной функции ![]() в точке х
в точке х![]() и обозначается
и обозначается
![]() .
.
Операция вычисления производной называется операцией дифференцирования.
Образно говоря, равенство
![]() означает, что производная
означает, что производная
![]() функции
функции ![]() в точке х
в точке х![]() равна скорости изменения переменной у
относительно переменой
равна скорости изменения переменной у
относительно переменой ![]() в указанной точке.
в указанной точке.
Определение 2. Функция ![]() , заданная в некоторой окрестности
, заданная в некоторой окрестности
![]() точки
точки ![]() R называется дифференцируемой в
этой точке, если ее приращение
R называется дифференцируемой в
этой точке, если ее приращение
![]() ,
,
![]() представимо в этой окрестности в виде
представимо в этой окрестности в виде
![]() , где
, где ![]() - постоянная,
О(
- постоянная,
О(![]() х) - бесконечно малая более высокого порядка, чем
х) - бесконечно малая более высокого порядка, чем ![]() х.
х.
Линейная функция
![]() (аргумента
(аргумента ![]() х) называется дифференциалом
функции
х) называется дифференциалом
функции ![]() в точке х
в точке х![]() и обозначается df(x
и обозначается df(x![]() или dy.
или dy.
Таким образом, ![]() у = dy + О(
у = dy + О(![]() х),
х),
![]() .
.
Можно доказать следующую теорему:
Теорема 1. Функция дифференцируема в некоторой точке в том и только том случае, когда в этой точке имеет конечную производную.
Учитывая определение 2 и утверждение теоремы, в качестве определения дифференцируемой функции может быть принято следующее:
Определение 3. Если функция у ![]() имеет производную в точке
имеет производную в точке ![]() , то
говорят, что при данном значении
, то
говорят, что при данном значении ![]() функция дифференцируема.
функция дифференцируема.
То есть существование производной функции ![]() в точке х
в точке х![]() равносильно ее дифференцируемости в этой точке.
равносильно ее дифференцируемости в этой точке.
Теорема 2. Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.
Обратная теорема не верна: существуют функции, непрерывные в некоторой точке, но не дифференцируемые в этой точке.
Теорема Ферма.
Если функция определена в некоторой окрестности точки ![]() , принимает в
этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и
имеет в точке х
, принимает в
этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и
имеет в точке х![]() производную, то эта производная равна нулю.
производную, то эта производная равна нулю.
Теорема Ролля.
Если функция ![]()
1) непрерывна на отрезке [![]() ]
]
2) имеет в каждой точке интервала ![]() конечную производную,
конечную производную,
3) принимает равные значения на концах отрезка [![]() ], то есть f(a) = f(b), то существует,
по крайней мере, одна такая точка
], то есть f(a) = f(b), то существует,
по крайней мере, одна такая точка ![]()
![]() , что
, что
![]() .
.
Теорема Лагранжа.
Если функция ![]() непрерывна на отрезке [
непрерывна на отрезке [![]() ] и в каждой точке интервала
] и в каждой точке интервала ![]() имеет
конечную или определенного знака бесконечную производную, то существует
такая точка
имеет
конечную или определенного знака бесконечную производную, то существует
такая точка ![]()
![]() , что f(b) - f(a) = f
, что f(b) - f(a) = f ![]() (
(![]() (b - a).
(b - a).
Используя теорему Лагранжа, можно доказать следующие теоремы:
Условие постоянства функции
Теорема 3. (Условие постоянства функции) Пусть функция ![]() определена
и непрерывна на промежутке Х и во всех его внутренних точках имеет конечную
производную
определена
и непрерывна на промежутке Х и во всех его внутренних точках имеет конечную
производную![]() . Для того, чтобы
. Для того, чтобы ![]() была на указанном отрезке
постоянной, необходимое и достаточное условие
была на указанном отрезке
постоянной, необходимое и достаточное условие ![]() внутри Х.
внутри Х.
Следствие
Если две функции ![]() и
и ![]() определены и непрерывны в промежутке
Х и внутри него имеют конечные производные
определены и непрерывны в промежутке
Х и внутри него имеют конечные производные![]() и
и ![]() , причем
, причем
![]() (внутри Х), то эти функции на всем промежутке Х
отличаются лишь на постоянную:
(внутри Х), то эти функции на всем промежутке Х
отличаются лишь на постоянную:
![]() (C = const).
(C = const).
Теорема 4. (Признак монотонности функций)
Для того чтобы дифференцируемая на интервале функция возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательна (неположительна).
Если производная функция во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает) на этом интервале.
Теорема 5.
Если функции ![]() и
и ![]() непрерывны на отрезке [
непрерывны на отрезке [![]() ] и в каждой точке интервала
] и в каждой точке интервала ![]() имеют
конечные производные
имеют
конечные производные![]() ,
,![]() , причем
, причем
![]() для
для
![]() , а f(а)
, а f(а) ![]() g(а), тогда для любой точки
g(а), тогда для любой точки ![]() выполняется неравенство
выполняется неравенство
![]() .
.
Замечание
На основании утверждения теоремы 5 для того, чтобы доказать неравенство
f(x) ![]() 0 при х
0 при х ![]() 0, достаточно доказать, что f(0)
0, достаточно доказать, что f(0) ![]() 0 и
0 и ![]() (х)
(х) ![]() 0 при х
0 при х ![]() 0. А для того, чтобы доказать
неравенство
0. А для того, чтобы доказать
неравенство ![]() при
при ![]() , можно воспользоваться второй
производной
, можно воспользоваться второй
производной
![]() и
и
![]() при
при ![]() и т.д.
и т.д.
С помощью производной можно также определить число корней того или иного уравнения. Один из возможных приемов основан на следующей теореме:
Теорема 6.
Если функция определена и непрерывна на отрезке и во всех его внутренних точках имеет конечную производную, то между любыми двумя корнями этой функции, расположенными на отрезке, имеется хотя бы 1 корень ее производной.
Рассмотренные теоретические положения используются при решении задач.
Задача 1. Докажите тождество 3arcsin x - arccos(3![]() 4
4![]() ) =
) = ![]() , если
, если
![]() .
.
Решение. Рассмотрим функцию ![]() 3arcsinx - arccos(3
3arcsinx - arccos(3![]() 4
4![]() на отрезке [
на отрезке [
![]() ]. Докажем, что f(х) = с, с = const. Для этого достаточно доказать, что
]. Докажем, что f(х) = с, с = const. Для этого достаточно доказать, что
![]() (т.3)
(т.3)
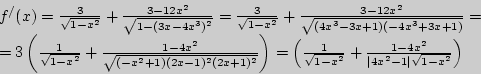
Если
![]() <
<![]() , то
, то
![]() следовательно,
следовательно, ![]() и
и ![]() . Для определения значения
. Для определения значения
![]() вычислим значение функции
вычислим значение функции ![]() в произвольной точке интервала
в произвольной точке интервала
![]() . Пусть
. Пусть ![]() , тогда
, тогда
![]() и
и ![]() .
.
Вычислим значение функции на концах заданного отрезка.
Таким образом, тождество верно при любом
![]() .
.
Задача 2. Найдите сумму
![]() .
.
Решение. Представив искомую сумму в виде
![]() , заметим, что
, заметим, что
![]() .
.
Используя формулу суммы ![]() членов геометрической прогрессии, получим,
членов геометрической прогрессии, получим,
![]()
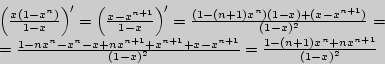
Итак, искомая сумма имеет вид
![]() .
.
Используя полученную формулу, можно, например, вычислить
а)
![]() ,
,
b)
![]() .
.
Задача 3. Найдите сумму:
![]()
Решение. Используя результат, полученный в примере 2,
заметим, что
![]()
Тогда
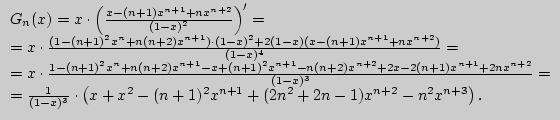
Задача 4. Решите уравнение:
![]()
Решение. Очевидно, что ![]() - корень уравнения.
Докажем, что уравнение других корней не имеет. Рассмотрим функцию
- корень уравнения.
Докажем, что уравнение других корней не имеет. Рассмотрим функцию
![]()
Найдем производную:
![]() R.
R.
Для функции ![]() точка
точка ![]() является точкой минимума, в которой функция
принимает наименьшее значение. Значит, для всех
является точкой минимума, в которой функция
принимает наименьшее значение. Значит, для всех ![]() , отличных от нуля,
, отличных от нуля,
![]() >
>![]() .
.
Ответ: ![]()
Задача 5. Решите уравнение:
![]()
Решение.
I способ.
Преобразуем уравнение к виду:
Рассмотрим функции
![]() и
и
![]() при
при
![]() .
.
Сравним множества значений этих функций. Очевидно, что
![]() .
.
Найдем ![]() с использованием производной.
с использованием производной.
![\begin{displaymath}
{g}'(x) = \frac{1 - \sqrt[4]{(2x - 1)^3}}{\sqrt[4]{(2x - 1)^3}}.
\end{displaymath}](img105.png)
Функция ![]() непрерывна на промежутке
непрерывна на промежутке
![]() и имеет на нем единственную критическую точку
и имеет на нем единственную критическую точку ![]() , в которой
достигает своего наибольшего значения.
, в которой
достигает своего наибольшего значения.
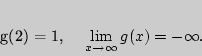
Значит,
![]() .
.
Следовательно, решение уравнения находим из решения системы:
Ответ:![]()
II способ.
Рассмотрим функцию
![]() , при
, при
![]() .
.
Функция ![]() непрерывна на промежутке
непрерывна на промежутке
![]() и является возрастающей,
и является возрастающей,
![]() .
. ![]() - является точкой
минимума функции
- является точкой
минимума функции ![]() , в которой функция принимает наименьшее значение,
ровное нулю. Следовательно, для всех
, в которой функция принимает наименьшее значение,
ровное нулю. Следовательно, для всех
![]() >
>![]() .
.
Таким образом, исходное уравнение имеет единственный корень ![]() .
.
Ответ: ![]() .
.
Задача 6. Докажите, что уравнение
![]() может иметь не более трех различных корней.
может иметь не более трех различных корней.
Решение. Рассмотрим функцию
![]() . Функция
. Функция ![]() является дифференцируемой на R. Предположим, что
функция имеет более трех различных корней, например, четыре. Тогда
является дифференцируемой на R. Предположим, что
функция имеет более трех различных корней, например, четыре. Тогда ![]() должна иметь не более трех различных корней (т.6), то есть
должна иметь не более трех различных корней (т.6), то есть
![]() обращается в нуль не менее трех раз.
обращается в нуль не менее трех раз.
Функция ![]() дифференцируема на R. Ее производная обращается в
нуль не менее двух раз. Тогда
дифференцируема на R. Ее производная обращается в
нуль не менее двух раз. Тогда
![]() имеет не менее двух
нулей, а ее производная
имеет не менее двух
нулей, а ее производная
![]() не менее одного нуля. Но функция
не менее одного нуля. Но функция
![]() нулей не имеет. Получили противоречие. Значит, сделанное
предположение неверно, функция
нулей не имеет. Получили противоречие. Значит, сделанное
предположение неверно, функция ![]() более трех различных корней иметь не
может. Таким образом, заданное уравнение может иметь не более трех различных
корней.
более трех различных корней иметь не
может. Таким образом, заданное уравнение может иметь не более трех различных
корней.
Производную можно использовать при доказательстве и решении неравенств.
Задача 7. Доказать, что
![]() при
при ![]() .
.
Доказательство. Докажем справедливость следующих неравенств:
![]() (2) и
(2) и
Для доказательства неравенства (2) рассмотрим функцию
![]()
Следовательно, ![]() (т. 5.)
(т. 5.)
Неравенство (2) верно.
Для доказательства неравенства (1) рассмотрим функцию
![]() .
.
Значит, ![]() на рассматриваемом множестве.
на рассматриваемом множестве.
Неравенства (2) и (1) справедливы.
Задача 8. Докажите, что для
![]()
![]() .
.
Доказательство. Докажем неравенство
![]() , которое на указанном промежутке равносильно заданному.
, которое на указанном промежутке равносильно заданному.
Рассмотрим функцию
![]() на интервале
на интервале
![]() и докажем, что на нем она возрастает. Для этого достаточно
доказать что
и докажем, что на нем она возрастает. Для этого достаточно
доказать что ![]() .
.
Так как
![]() при
при
![]() , то покажем, что
, то покажем, что
![]() . Рассмотрим функцию
. Рассмотрим функцию
![]() ,
,
Заметим, что
![]() .
.
Значит, ![]() (т. 5).
(т. 5).
Следовательно, ![]() и
и ![]() является возрастающей на интервале
является возрастающей на интервале
![]() . Для
. Для
![]() справедливо неравенство
справедливо неравенство
![]() или
или
![]() .
.
Задача 9. Определите, какое из чисел больше:
![]() или
или
![]() .
.
Решение. Предположим, что
![]() , тогда и
, тогда и
![]() , отсюда
, отсюда
![]() . Чтобы доказать или опровергнуть это неравенство, рассмотрим функцию
. Чтобы доказать или опровергнуть это неравенство, рассмотрим функцию
![]() , где
, где ![]() и определим характер ее монотонности.
и определим характер ее монотонности.
Задача 10. Докажите, что
![]() .
.
Решение. Рассмотрим функцию
![]() ,
которая на промежутке
,
которая на промежутке
![]() является
возрастающей (см. пример 8). Будут справедливы неравенства
является
возрастающей (см. пример 8). Будут справедливы неравенства
Задача 11. Сравните числа а) ![]() и
и ![]() ,
,
b) ![]() и
и ![]() .
.
Решение.
Исследуем ![]() на монотонность.
на монотонность.
При ![]() знаменатель дроби положительный, а для определения знака
числителя достаточно заметить, что функция
знаменатель дроби положительный, а для определения знака
числителя достаточно заметить, что функция ![]() возрастает.
Следовательно, при
возрастает.
Следовательно, при
![]() ,
, ![]() убывает и
убывает и
![]() .
.
b) Сравним числа ![]() и
и ![]() . Для этого рассмотрим
функцию
. Для этого рассмотрим
функцию
![]() ,
,
![]() и,
следовательно функция
и,
следовательно функция ![]() является неубывающей на области определения.
является неубывающей на области определения.
Таким образом,
![]() .
.
Пример 12. Докажите, что
![]() .
.
Решение. Заметим, что данное неравенство является
частным случаем следующего неравенства:
![]() N.
N.
Для доказательства рассмотрим на отрезке ![]() функцию
функцию ![]() ,
которая удовлетворяет всем условиям теоремы Лагранжа. Значит, найдется такая
точка
,
которая удовлетворяет всем условиям теоремы Лагранжа. Значит, найдется такая
точка
![]() , что
, что
![]() .
.
Значит,
![]() и
и
![]() .
.
Таким образом,
![]() .
.
При ![]() справедливо неравенство
справедливо неравенство
![]() .
.
1. Докажите тождества:
2. При каком значении ![]() равенство
равенство
![]() является тождеством?
является тождеством?
3. Найдите сумму:
4. Найдите область определения функции:
5. Найдите положительные корни уравнения
![]() .
.
6. Сколько корней имеет уравнение:
7. Решите уравнения:
8. Докажите, что уравнение
![]() имеет единственное решение.
имеет единственное решение.
9. При каких значениях ![]() уравнение
уравнение
![]() имеет 3 корня на
отрезке
имеет 3 корня на
отрезке ![]() ?
?
10. При каких значениях ![]() все три корня уравнения
все три корня уравнения
![]() действительны?
действительны?
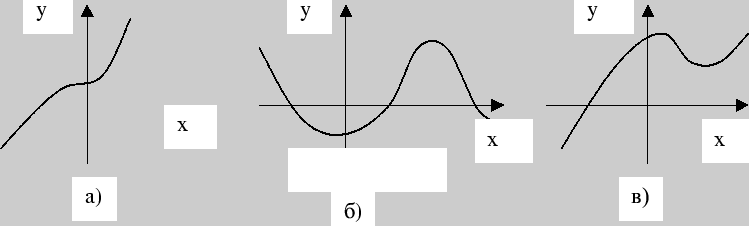
11. По эскизу графика
![]() (рис. 1) определите знаки
(рис. 1) определите знаки
![]()
12. Докажите, что при ![]()
13. Докажите, что
при ![]() .
.
14. Докажите, что
![]() при
при ![]() .
.
15. Докажите, что при
![]() .
.
16. Докажите, что
если
![]() , то
, то
![]() ;
;
если
![]() , то
, то
![]() .
.
17. Докажите, что
![]() при
при ![]() .
.
18. Докажите, что
![]() при
при ![]() .
.
19. Докажите неравенство
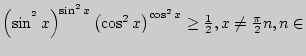 Z.
Z.
20. Определите, какое из чисел больше
21. Решите неравенство:
;
22. Докажите, что все корни производной многочлена
![]() различны.
различны.
23. Докажите неравенство
![]() при
при
![]() N,
N, ![]() N.
N.
24. Докажите, что
![]() .
.