Далее: Графическое изображение результатов Вверх: Основы теории погрешностей Назад: Основы теории погрешностей

Методы обработки результатов измерений, содержащих случайную ошибку

Пусть в одних и тех же условиях проделано $n$ измерений и $x_i$ -- результат $i$-го измерения. Наиболее вероятное значение измеряемой величины -- ее среднее (арифметическое) значение.

$${\overline{x}}={x_1+x_2+\ldots+x_n\over n}={1\over n}\sum\limits_{i=1}^n{x_i} .$$ (1)

Величина ${\overline{x}}$ стремится к истинному значению $x_o$ измеряемой величины при $n\rightarrow\infty$. Средней квадратичной ошибкой отдельного результата называется величина:

$$S_n=\sqrt{\sum\limits_{i=1}^n{(\overline{x}-x_i)^2}\over n-1} .$$ (2)

При $n\rightarrow\infty$ $S_n$ стремится к постоянному пределу $\sigma$:

$$\sigma=\lim\limits_{n\rightarrow\infty}{S_n} .$$ (3)

Величина $\sigma^2$ называется дисперсией измерений. С увеличением $\sigma$ уменьшается точность измерений. Величина $\sigma$ служит основным параметром, определяющим вид кривой распределения случайных ошибок. Нормальный закон распределения ошибок (распределение Гаусса) выражается формулой:

$$y={1\over\sigma\sqrt{2\pi}}e^{-{(\Delta x)^2\over 2\sigma^2}} ,$$ (4)

где $\Delta x=\overline{x}-x_i$ -- отклонение от истинного значения, $e$ -- основание натурального логарифма ($e=2,72\ldots$).

Возрастание точности измерений при росте числа измерений иллюстрируется величиной среднеквадратичной ошибки среднего арифметического:

$$S_{n\overline{x}}=\sqrt{\sum\limits_{i=1}^n{(\overline{x}-x_i)^2}\over n(n-1)}={S_n\over \sqrt{n}} .$$ (5)

Вероятность $\alpha$ того, что истинное значение находится внутри некоторого интервала от $\overline{x}-\Delta x$ до $\overline{x}+\Delta x$, называется доверительной вероятностью (коэффициентом надежности), а интервал -- доверительным интервалом.

Окончательный результат измерений запишется в виде:

$$x=\overline{x}\pm S_{n\overline{x}} .$$ (6)

При малом числе измерений заданному значению $\alpha$ соответствует несколько больший доверительный интервал. Множители, определяющие величину интервала в долях $S_{n\overline{x}}$ в зависимости от коэффициента надежности $\alpha$ и числа измерений $n$, называются коэффициентами Стьюдента -- $t_{\alpha n}$. Они находятся по специальным таблицам.

Конечный результат представляется в виде:

$$x=\overline{x}\pm t_{\alpha n}\cdot S_{n\overline{x}} .$$ (7)

Точность зависит от числа измерений $n$, однако существенно увеличивается до тех пор, пока случайная ошибка не станет сравнимой с систематической.

При косвенных измерениях для вычисления случайной ошибки $\Delta z$ функции $z=f(x,y)$ , где $x$ и $y$ -- непосредственно измеряемые независимые величины со среднеквадратичной ошибкой отдельного измерения соответственно $\Delta x$ и $\Delta y$. Среднеквадратичную ошибку для произвольной функции можно определить по правилам дифференцирования сложной функции:

$$dz={\partial z\over\partial x}dx+{\partial z\over\partial y}dy .$$ (8)

При не слишком высокой точности измерительных приборов случайными ошибками можно пренебречь по сравнению с погрешностью измерительного прибора. Для получения результата достаточно одного отсчета, при этом максимальная возможная ошибка результата задается классом точности прибора (классом точности называется максимальная абсолютная ошибка в процентах от всей действующей шкалы прибора).

В общем случае формулы для расчета максимальных ошибок могут быть выражены следующим образом:

$$\text{если}\quad z=f(x_1,x_2,\ldots,x_n) ,$$

то

$$\Delta z=\sum\limits_{i=1}^n{\vert{\partial f\over\partial x}\delta x_i\vert} ,$$ (9)

где $\delta x_i$ и $\Delta z$ -- абсолютные погрешности соответствующих величин.

При обработке результатов измерений предлагается следующий порядок операций.

При прямых измерениях:

1. Вычисляют среднее значение из $n$ измерений:
   
   $${\overline{x}}={x_1+x_2+\ldots+x_n\over n}={1\over n}\sum\limits_{i=1}^n{x_i} .$$
   
   

2. Находят погрешности отдельного измерения:
   
   $$\Delta x=\overline{x}-x_i .$$
   
   

3. Вычисляют квадраты погрешностей отдельных измерений:
   
   $$(\Delta x_1)^2,(\Delta x_2)^2,(\Delta x_3)^2,\ldots,(\Delta x_n)^2.$$
   
   

4. Определяют среднеквадратичную погрешность среднего арифметического:
   
   $$S_{n\overline{x}}=\sqrt{\sum\limits_{i=1}^n{(\Delta x)^2}\over n(n-1)} .$$
   
   

5. Задают коэффициент надежности $\alpha$.
6. Определяют коэффициент Стьюдента $t_{\alpha n}$ для заданной надежности $\alpha$ и числа произведенных измерений $n$ (по таблице).
7. Находят доверительный интервал (погрешность результата измерений):
   
   $$\Delta x=t_{\alpha n}\cdot S_{n\overline{x}} .$$
   
   

8. Если величина погрешности результата измерений сравнима с погрешностью прибора $\delta$, то в качестве границы доверительного интервала следует взять величину
   
   $$\Delta x=t_{\alpha n}\cdot S_{n\overline{x}}+\delta .$$
   
   

9. Окончательный результат записывают в виде:
   
   $$x=\overline{x}\pm\Delta x ,\quad\text{при}\quad\alpha=0,95 .$$
   
   

10. Оценивают относительную погрешность результата измерений:
    
    $$\varepsilon={\Delta x\over\overline{x}}\cdot 100\% .$$
    
    

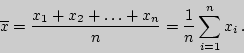
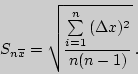
При косвенных измерениях:

1. Для каждой серии величин, входящих в определения искомой величины, проводится обработка в описанной выше последовательности. При этом для всех измеряемых величин задают одно и то же значение надежности $\alpha$.
2. Оценивается точность результата по формулам (8) и (9), где производные вычисляются при средних значениях величин.

   Для упрощения вычислений применяют следующую последовательность операций:

   -

   логарифмируют расчетную формулу;

   -

   находят полный дифференциал функции;

   -

   заменяют знак дифференциала $d$ на приращение $\Delta$, знаки выбирают так, чтобы величина относительной ошибки была максимальной.

3. Окончательный результат записывают как
   
   $$f(A,B,C,\ldots)=f(\overline{a},\overline{b},\overline{c},\ldots)\pm\Delta f .$$
   
   

4. Определяют относительную погрешность результата серии косвенных измерений:
   
   $$\varepsilon={\Delta f\over f}\cdot 100\% .$$
   
   

5. При практических вычислениях следует руководствоваться следующим правилами:

   -

   ошибка при вычислении результата должна быть примерно в 10 раз меньше суммарной ошибки измерений;

   -

   не следует приводить величину ошибки с точностью менее 10%. В большинстве случаев можно ограничиться только одной значащей цифрой. В случае, если эта значащая цифра мала или если среднеквадратичная ошибка получена из достаточно большого числа измерений, имеет смысл давать ошибку с двумя значащими цифрами.

Далее: Графическое изображение результатов Вверх: Основы теории погрешностей Назад: Основы теории погрешностей