Далее: §9. Приближенные формулы для Вверх: Глава II. Случайные события Назад: §7. Формула полной вероятности

§8. Схема Бернулли

Под схемой Бернулли понимают конечную серию $n$ повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают $p=P(Y)$, а непоявления (неудачи) его $P(H)= q = 1- p$. Я. Бернулли установил, что вероятность ровно $m$ успехов в серии из $n$ повторных независимых испытаний вычисляется по следующей формуле:

$$P_n (m) = C_n^m \cdot p^m \cdot q^{n - m}.$$

То значение $m_{0}$, при котором число $P_{n}(m)$ является максимальным из множества {$P_{n}(m)$}, называется наивероятнейшим, и оно удовлетворяет условию

np - q $\le$ m$_{0 }$$\le$ np+ p, $(m_0 \in {\rm {\bf {\rm Z}}}).$

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из $k$ событий с вероятностью $p_{i}$ ( $i= 1, 2, \ldots,k)$. Вероятность появления $m_{1}$ раз первого события и $m_{2}$ - второго и $m_{k}-k$-го находится по формуле

$$P_n (m_1 ,m_2 ,...,m_k ) = {\displaystyle n!\over\displaysty... ...m_k !} \cdot p^{m_1 } \cdot p^{m_2 } \cdot ... \cdot p^{m_k }.$$

При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

$$P_n (m) \approx {\displaystyle \lambda ^m\over\displaystyle m!}e^{ - \lambda }, {\text{где} } \lambda = np.$$

Таблица значений функции ${\displaystyle \lambda ^m\over\displaystyle m!}e^{ - \lambda }$имеется в приложении 3.

Пример 36. Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из 8 единиц. Каждый объект может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что хотя бы один из объектов будет потерян.

Решение. Пусть событие $A$ = {потерять системой радиолокационных станций хотя бы один объект}, тогда $P(A)=P_{8}$(1)$+ P_{8}$(2)+...+ P$_{8}$(8)$.$

Проще найти вероятность противоположного события - ни один объект не потерян.

$$P(\bar {A}) = P_8 (0) = C_8^0 \cdot (0,1)^0 \cdot (0,9)^8 \approx 0,43 {\text{ и}}\ P(A) = 1 - P(\bar {A}) \approx 0,57.$$

Пример 37. На I курс педуниверситета поступило 1100 студентов. Найти наиболее вероятное число первокурсников ЯГПУ, родившихся в один день - в день знаний 1 сентября, и вероятность этого события.

Решение. В нашем случае $p\approx {\displaystyle \displaystyle 1\over\displaystyle \displaystyle 365},$$n=1100.$ Используем соотношение для наивероятнейшего числа $m_{0}$:

$$1100 \cdot {\displaystyle 1\over\displaystyle 365} - {\displ... ...r\displaystyle 365} + {\displaystyle 1\over\displaystyle 365}.$$

Учитывая, что $m_{0}$ целое число, получаем $m_{0}$= 3.

Найдем теперь P$_{1100}$(3), используя теорему Пуассона и то, что $\lambda = 1100 \cdot {\displaystyle \displaystyle 1\over\displaystyle \displaystyle 365} \approx 3$:

$P_{1100} (3) \approx {\displaystyle \displaystyle 3^3\over\displaystyle \displaystyle 3!} \cdot {\text е}^{ - 3} \approx 0,22$(см. таблицу приложения 3).

Пример 38. Сколько раз придется бросать игральную кость, чтобы наивероятнейшее число появления шестерки было бы 10?

Решение. По условию задачи имеем наивероятнейшее число $m_{0}$= 10 и вероятность выпадения шестерки при одном подбрасывании игральной кости $p= {\displaystyle \displaystyle 1\over\displaystyle \displaystyle 6},$тогда $n \cdot {\displaystyle \displaystyle 1\over\displaystyle \displaystyle 6} - {\d... ...aystyle 6} + {\displaystyle \displaystyle 1\over\displaystyle \displaystyle 6}.$Это двойное неравенство равносильно системе двух неравенств:

$$\left\{ {\begin{array}{l} n \cdot {\displaystyle \displayst... ... \ge 10 \\ \end{array}} \right.\qquad\qquad 59 \le n \le 65.$$

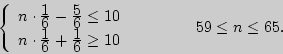
Пример 39. В Ярославле 50% школьников изучают английский язык, 30% - немецкий и 20% - французский. Какова вероятность того, что из девяти слушателей подготовительного отделения физмата четверо изучали в школе английский язык, трое - немецкий и двое - французский?

Решение. По условию задачи $n$ = 9, $m_{1}$ = 4, $p_{1}$ = 0,5, $m_{2}$ = 3, $p_{2}$ = 0,3, $m_{3}$ = 2, $p_{3}$ = 0,2 и

$$P_9 (4,3,2) = {\displaystyle 9!\over\displaystyle 4! \cdot 3! \cdot 2!}(0,5)^4 \cdot (0,3)^3 \cdot (0,2)^2 \approx 0,0085.$$

Пример 40 (задача С. Пепайса). Пепайс предложил Ньютону следующую задачу. Какое из событий более вероятно:

$A$ = {появление по крайней мере одной шестерки при подбрасывании 6 костей},

$B$ = { появление хотя бы двух шестерок при подбрасывании 12 костей} и

$C$ = {появление не менее трех шестерок при бросании 18 костей}?

Решение. Проще находить, а затем сравнивать вероятности противоположных событий. Воспользуемся теоремой Пуассона для нахождения $P(\bar {A}),$ $P(\bar {B})$ и $P(\bar {C}).$

$$P(\bar {A}) = P_6 (0) \approx {\displaystyle \lambda ^0\over... ...a = np = 6 \cdot {\displaystyle 1\over\displaystyle 6} = {1; }$$

$$P(\bar {B}) = P_{12} (0) + P_{12} (1) \approx {\displaystyle... ... \lambda = 12 \cdot {\displaystyle 1\over\displaystyle 6} = 2;$$

$$P(\bar {C}) = P_{18} (0) + P_{18} (1) + P_{18} (2) \approx {... ... \lambda = 18 \cdot {\displaystyle 1\over\displaystyle 6} = 3.$$

Отсюда $P(\bar {A}) < P(\bar {B}) < P(\bar {C})$, или $1- P(A) < 1 - P(B) < 1 - P(C)$, т.е.

$P(A) > P(B) > P(C)$.

Вопросы для самоконтроля

1. Какие повторные испытания называются независимыми? Примеры.
2. Что называют схемой Бернулли?
3. Сколько ветвей содержит дерево исходов при четырех испытаниях схемы Бернулли?
4. Какие способы получения формулы Бернулли вы знаете?
5. В чем заключаются обобщения схемы Бернулли?
6. Какое число называют наивероятнейшим? Как его найти?
7. Сколько существует наивероятнейших чисел?
8. В каком случае наивероятнейшее число равно нулю?
9. В чем смысл теоремы Пуассона?

Задачи

I 71. Что вероятнее: выиграть у равносильного противника в теннис два сета из четырех или три из шести?

  72. Пассажиру, путешествующему в купейном вагоне, удобно, когда все его попутчики - лица того же пола, что и он. Сколько процентов таких пассажиров случайно попадают в удобные условия?

  73. В Ярославской области 60% школьников изучают английский язык, 30% - немецкий и 10% - французский. Какова вероятность того, что из десяти слушателей подготовительного отделения физмата пятеро изучали в школе английский язык, трое - немецкий и двое - французский?

  74. В семье 4 детей. Найдите вероятность того, что среди них поровну мальчиков и девочек.

  75. Найдите наибольшее вероятное число выпадания шести очков при 100 подбрасываниях игральной кости.

  76. Среди облигаций займа 10% выигравших. Найдите вероятность того, что из четырех взятых облигаций:

а) все облигации выиграют;

б) хотя бы одна облигация выиграет;

в) выиграет ровно одна облигация.

II 77. Чему равна вероятность наступления события в каждом из 99 независимых испытаний, если наивероятнейшее число наступления события в этих испытаниях равно 60?

  78. (Задача де Мере). Сколько раз надо бросить пару игральных костей, чтобы с вероятностью, не меньшей ${\displaystyle \displaystyle 1\over\displaystyle \displaystyle 2},$ можно было утверждать, что хотя бы раз появится 12 очков?

III 79. Найдите вероятностным способом частичную сумму убывающей геометрической прогрессии.

  80. Контрольное задание состоит из десяти вопросов, предусматривающих ответы "да" и "нет". Подсчитать вероятность того, что студент, давший 8 верных ответов, знает 8 вопросов, если известно, что 10% студентов знают 6 вопросов, 20% студентов - 7 вопросов, 30% - 8 вопросов, а остальные знают более 8 вопросов.

Далее: §9. Приближенные формулы для Вверх: Глава II. Случайные события Назад: §7. Формула полной вероятности