Далее: §30. Блочные коды Вверх: Глава IV. Энтропия и Назад: §28. Информация и логические

§27. Кодирование и декодирование

Коды появились в глубокой древности в виде криптограмм, когда ими пользовались для засекречивания важного сообщения от тех, кому оно не было предназначено. Еще знаменитый греческий историк Геродот (V век до н.э.) приводил примеры писем, понятных лишь для одного адресата. Спартанцы имели специальный механический прибор, при помощи которого важные сообщения можно было писать особым способом, обеспечивающим сохранение тайны. Собственная секретная азбука была у Юлия Цезаря. В средние века и эпоху Возрождения над изобретением тайных шифров трудились философ Фрэнсис Бэкон, крупные математики того времени Франсуа Виет, Джероламо Кардано, Джон Валлис.

В этом разделе речь будет идти в основном об ином направлении в кодировании, которое возникло в близкую к нам эпоху. Связано оно с проблемой передачи сообщений по линиям связи, без которых (телеграфа, телефона, радио, телевидения и т.д.) немыслимо наше нынешнее существование. Зада-чей такого кодирования является сделать передачу сообщений быстрой, удобной и надежной. Предназначенное для этой цели кодирующее устройство сопоставляет каждому символу передаваемого текста, а иногда и целым словам или фразам (сообщениям) определенную комбинацию сигналов (применяемую для передачи по данному каналу связи), называемую кодом или кодовым словом. При этом операцию перевода сообщений в определенные последовательности сигналов называют кодированием, а обратную операцию, восстанавливающую по принятым сигналам (кодовым словам) передаваемые сообщения, - декодированием.

Исторически первый код, предназначенный для передачи сообщений, связан с именем изобретателя телеграфного аппарата Сэмюэля Морзе и известен как азбука Морзе. В этом коде каждой букве или цифре сопоставляется своя последовательность из кратковременных (называемых точками) и длительных (тире) импульсов тока, разделяемых паузами. Другой код, столь же распространенный в телеграфии (код Бодо), использует для кодирования два элементарных символа - импульс и паузу, при этом сопоставляемые буквам кодовые слова состоят из пяти таких сигналов.

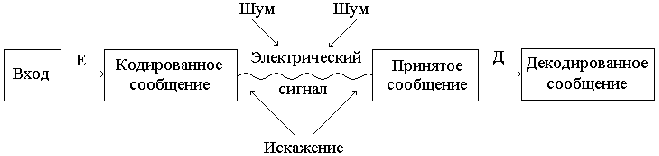
Общую схему передачи сообщений можно представить так:

Рис. 86

Коды, использующие два различных элементарных сигнала, называются двоичными. Удобно обозначать эти два сигнала 0 и 1. Тогда кодовые слова можно представлять как последовательность из нулей и единиц.

Пример 141. Как можно закодировать четыре сообщения $a$, $b$, $с$, $d$, используя только два сигнала, 0 и 1?

Решение. Один из вариантов кодирования может быть следующим: 00, 01, 10, 11. При таком кодировании вероятность появления сообщений не учитывалась или предполагалась равновероятность ($р = 0,25$). Между тем их появление в информационном тексте может происходить с различной частотой; предположим, вероятности появления сообщений равны:

$р = 0,4$; $р = 0,3$; $р = 0,2$; $р = 0,1$.

Учитывая вероятность сообщений, Фано предложил следующее оптимальное кодирование

Сообщения	$a$	$b$	$c$	$d$
Коды	1	01	001	000

Показателем экономичности кода служит средняя длина кодового слова (математическое ожидание длины кодового слова). Для кодировки сообщений первым способом средняя длина равна 2, а по методу Фано - 1,75. Следовательно, закодированный по методике Фано информационный текст окажется короче.

На первый взгляд, кодирование по методу Фано кажется избыточным, поскольку представленные коды можно сократить, например, так

Сообщения	$a$	$b$	$c$	$d$
Коды	1	0	01	00

Однако если возьмем следующий закодированный текст: 011001, то по последней таблице данный текст не может быть однозначно дешифрован, так как непонятно, что, собственно, подразумевается: сообщение $саdа$ или саbbа, или $bааdа$ и т.д. Расшифровка же текста по методу Фано однозначна - $bас$. Такой код называется префиксным. Никакое кодовое слово префиксного кода не является началом другого кодового слова. Наряду с кодом Фано, существует префиксное кодирование по методу Хаффмана, экономность которого еще выше.

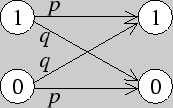
Пусть двоичные сигналы 0, 1 последовательно передаются по каналу связи на приемник, тогда вероятности перехода в двоичном симметричном канале представлены следующим образом:

Рис. 87

Для защиты передаваемых текстов от помех используются корректирующие коды, которые основаны на информационной избыточности. Самый простой способ создания избыточности достигается многократным дублированием передаваемых символов, т.е. образованием символьных блоков: $0 \to 00000, 1 \to 11111$. В случае сбоя решение при дешифровке принимается по большинству оставшихся символов в блоке.

Существует очень простая, но эффективная защита информационного текста от единичного сбоя, которая требует минимальной избыточности в один дополнительный символ. Это проверка на четность. При кодировании к тексту добавляется 0 или 1 в зависимости от четности или нечетности суммы единиц в тексте. Если при декодировании обнаружится нечетное число единиц, значит, текст был принят неверно.

Процедура кодирования с помощью двух символов может быть представ-лена бинарным деревом. Длина ветвей, равная длине каждого кодового слова, определяет естественные порядковые уровни. Например, рассмотренный выше код Фано может быть представлен следующим бинарным деревом:

Рис. 88

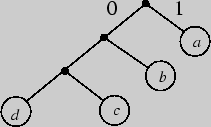
В нашем дереве символу 0 соответствует ребро, отклоняющееся влево, а символу 1 - ребро, отклоняющееся вправо.

Кодирование и декодирование используем для демонстрации передачи и хранения необходимой информации. Такой целостный взгляд на предложен-ную цепочку не только обогащает студента новыми знаниями, но и показы-вает целостность математики. Так, рассматриваемый материал дает представ-ление, сколь широки и разнообразны связи теории кодирования и декоди-рования с разными разделами математики (алгебра, геометрия, комбинатор-ный анализ) и как порой абстрактные математические теории могут с успе-хом применяться для решения практических задач.

Двоичным $(m,n)$ - кодом называется пара, состоящая из схемы кодирования Е: $2^{m} \to 2^{n}$ и схемы декодирования Д: $2^{ n } \to 2^{m}$, где $2^{n}$ - множество всех двоичных последовательностей длины $n$. Функции Е и Д выбираются так, чтобы функция $H = E \diamondsuit T \diamondsuit \mbox{Д}$ ($T$ - "функция ошибок") с вероятностью, близкой к единице, была тождественной.

Коды делятся на два класса. Коды с исправлением ошибок имеют целью правильно восстановить с вероятностью, близкой к единице, посланное сообщение. Коды с обнаружением ошибок имеют целью выявить с вероятностью, близкой к единице, наличие ошибок.

Пример 142. Построить схему кодирования и декодирования (3,4)-кода с обнаружением ошибок, основанного на принципе проверки четности.

Решение. Схему кодирования определим следующим образом:

Е: 000 $\to$ 0000; 001 $\to$ 0011; 010 $\to$ 0101; 100 $\to$ 1001;

011$\to$ 0110; 101 $\to$ 1010; 110 $\to$ 1100; 111 $\to$ 1111,

а схему декодирования :

Д: b $\to$ c, где $b_{i }$= $c_{i}$ при i = 1, 2, 3 и если $\sum\limits_{i = 0}^4 {b_i }$ нечетна, то приемник укажет наличие ошибки передачи.

Пример 143. Найти долю ошибочных сообщений, оставшихся незамеченными, относительно всех ошибочных сообщений для кода из предыдущего примера.

Решение. Приемник укажет наличие ошибки передачи, если сумма $\sum\limits_{i = 1}^4 {b_i }$ окажется нечетной и доля неверно принятых сообщений будет $q^4 + 4q^3p + 6q^2p^2 + 4qp^3$ (четыре, три, две или одна ошибка). Из них незамеченными окажутся только ошибки в двух или четырех знаках, не изменяющие четности. Следовательно, доля ошибочных сообщений, оставшихся незамеченными, составляет

$${\displaystyle q^4 + 6q^2p^2\over\displaystyle q^4 + 4q^3p +... ...style q^3 + 6qp^2\over\displaystyle q^3 + 4q^2p + 6qp + 4p^3}.$$

Пример 144. На сколько снижается вероятность ошибки приема одного символа в $(m,3m)$-коде с тройным повторением?

Решение. В нашем случае схема кодирования следующая:

C : $a \to b=a_{1}a_{2}\ldots a_{m}a_{1}a_{2}\ldots a_{m}a_{1}a_{2}\ldots a_{m}$, а декодирования: D : $b \to c$ и $c_{i}$ выбирается по принципу большинства (два или три раза встречающиеся) из тройки $b_{i }$, $b_{i + m}$, $b_{i + 2m}$. В этом случае вероятность правильного приема символа равна $p^{3}+3p^{2}q$, а ошибочного - $3pq^{2}+q^{3}$.

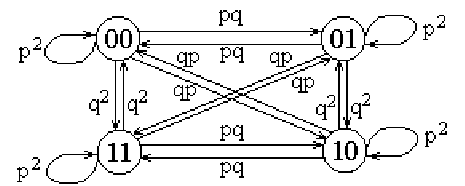
Пример 145. Найти граф цепи Маркова вероятностей приема двоичного (2,2)-кода.

Решение. Учитывая, что

Рис. 89

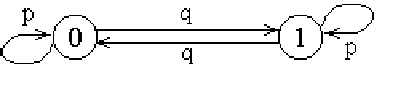
получаем искомый граф:

Рис. 90

Вопросы для самоконтроля

1. Что понимают под кодированием сообщения?

2. Приведите простейшие примеры кодовых сообщений.

3. Что называется основанием кода?

4. Какие коды называются равномерными?

5. Что понимают под экономностью кода?

6. Назовите условия однозначно декодируемых кодов.

7. Двоичные коды.

8. Что понимают под матрицей цепи Маркова вероятностей приема кода?

Задачи

I 281. Постройте схему кодирования и декодирования для (2,3)-кода, основанном на схеме проверки четности.

282. Для кода из предыдущего примера найти долю не замеченных при декодировании ошибок.

283. Найдите вероятность ошибки для $(m,5m)$-кода с пятикратным повторением и декодированием по принципу "большинства голосов".

284. Найдите вероятность ошибки при конкретной передаче и декодированием по принципу "большинства голосов".

285. Найдите матрицу цепи Маркова вероятностей приема двоичного кода (3,3).

286. Найдите матрицу цепи Маркова вероятностей приема двоичного кода (1,3) с исправлением ошибки.

II 287. Найдите матрицу цепи Маркова вероятностей приема двоичного кода (2,3) с обнаружением ошибки.

288. Предположим, что по двоичному симметричному каналу передаются строки длины 12.

а) Какова вероятность того, что ровно 5 символов будут приняты неправильно?

б) Какова вероятность того, что не больше 5 символов будут приняты неправильно?

в) Сколько имеется строк, отличающихся от данной не больше чем в трех позициях?

III 289. Пусть строка длины три передается по двоичному симметричному каналу, но вероятность ошибки меняется со временем так, что $i$-й сигнал принимается правильно с вероятностью $p_{i }(i = 1, 2, 3)$. Показать, что

а) матрица P = $(p_{ij})$ симметрична,

б) Р - стохастическая матрица.

290. Можно ли найти 32 двоичных слова длины 8 таких, что каждое отличается от другого слова не меньше, чем в трех позициях?

Далее: §30. Блочные коды Вверх: Глава IV. Энтропия и Назад: §28. Информация и логические