Далее: §27. Кодирование и декодирование Вверх: Глава IV. Энтропия и Назад: §27. Количество информации

§28. Информация и логические задачи

В этом параграфе понятие энтропии и информации применим к анализу некоторых занимательных логических задач. Во всех этих примерах нас будет интересовать некоторый объект из конечного множества $М$ однотипных объектов. Для выделения интересующего нас объекта (исхода опыта $\beta )$ будем использовать вспомогательные опыты $\alpha$. Каждый из этих опытов позволяет выделить те или иные исходы опыта $\beta$, отбрасывая ряд исходов множества $М$ как "ложные". Требуется указать наименьшее число вспомогательных опытов $\alpha$, необходимых для выяснения правильного ответа на интересующий нас вопрос, и описать, как именно можно быстрее всего найти этот ответ.

Как правило, вспомогательные опыты $\alpha$ ставятся так, чтобы они имели равновероятные исходы, что позволяет "снимать" наибольшую неопределенность.

Пример 136. Студенты из группы, в которой учится 25 человек, загадали одного из студентов. Сколько вопросов надо задать группе, чтобы отгадать выбранного студента, если группа на все вопросы отвечает "да" или "нет"?

Решение. Опыт $\beta$, состоящий в отгадывании студента, может иметь 25 равновероятных исходов, т.е. энтропия $H(\beta ) = \log 25 \approx 4,64$ бита. Рассмотрим опыт $A_{k}=\alpha _{1}\alpha _{2}$...$\alpha _{k}$, заключающийся в том, что опрашивающий задает k вопросов. Поскольку $\alpha _{i }$может иметь два исхода, то $Н(\alpha _{i})$ = 1 бит и $Н(А_{k}) \quad \le \quad k$ бит. С другой стороны, $I(A_{k}$,$\beta$) $\le \quad H(A_{k})$.

Для того, чтобы исход опыта $A_{k}$ полностью определял исход $\beta$, необходимо выполнение неравенства $I(A_{k}$,$\beta$) $\ge Н$($\beta$).

Отсюда $\log 25 = H(\beta ) \le I(A_k ,\beta ) \le H(A_k ) \le k,$ т.е. $k \ge \log 25 \approx 4,64$, или т.к. $k$ - целое число, то $k \ge 5$.

Для отгадывания задуманного студента разобьем группу примерно на две равные части (т.к. исходы опыта $\alpha _{1}$ должны быть примерно равновероятны, чтобы энтропия $Н(\alpha _{1})$ была наибольшей) и спросим, относится ли студент к одной из них.

Теперь, разбивая оставшуюся часть группы на возможно более близкие по численности части, мы определим задуманного студента с помощью пяти вопросов.

Другим способом отыскания задуманного студента может быть нумерация каждого студента в двоичной системе и расшифровка одного из двух символов, стоящего на каждом месте.

Пример 137. Сколько вопросов надо задать, чтобы отгадать месяц рождения незнакомого человека, если на все вопросы он будет отвечать "да" или "нет"?

Решение. Энтропию опыта $\beta$={угадывание месяца рождения незнакомого человека} находим по формуле Хартли $Н(\beta )$ = log12.

Тогда $k \ge H(\alpha _1 ) + H(\alpha _2 ) + ... + H(\alpha _k ) \ge I(\alpha _1 \alpha _2 ...\alpha _k ,\beta ) \ge H(\beta ) = \log 12.$

Отсюда $k \quad \ge$ log 12 и $k \quad \ge$ 4.

А определить искомый месяц можно, пронумеровав его в двоичной системе и расшифровывая один из двух символов, стоящий на каждом месте. Так, если незнакомец родился в мае - пятом по порядку месяце в году - то ему будет соответствовать следующая запись в двоичной системе: (0, 1, 0, 1), т.к. $5 = 0 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0.$

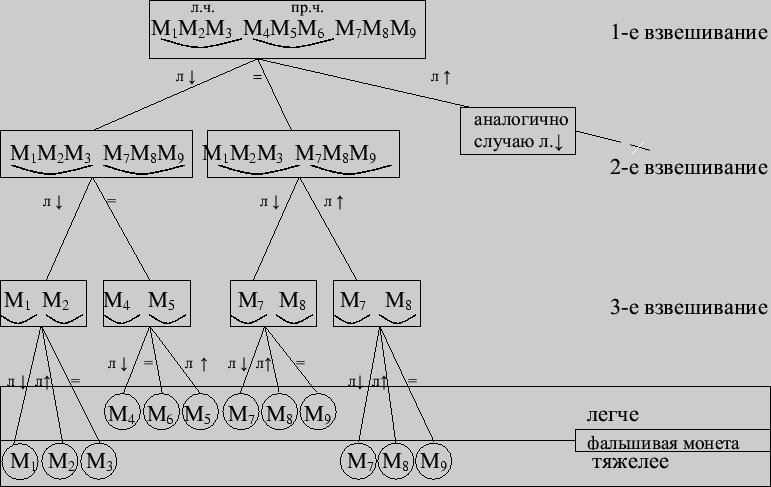
Пример 138. Имеется 9 монет одного достоинства, одна из которых фальшивая, отличающаяся от остальных по весу (причем неизвестно, легче она или тяжелее настоящих). Каково наименьшее число взвешиваний на чашечных весах без гирь, которое позволяет обнаружить фальшивую монету?

Решение. Опыт $\beta$, результат которого требуется определить, имеет 18 возможных исходов(каждая из 9 монет может оказаться фальшивой, и она может быть легче или тяжелее настоящей). Эти исходы естественно считать равновероятными, и тогда $Н(\beta ) = log18$, т.е. определение фальшивой монеты связано с получением информации, измеряющейся числом $log18$. Опыт $\alpha _{1}$, состоящий в одном взвешивании, может иметь три исхода, поэтому $H(\alpha _1 ) \le \log 3$ и информация $I(\alpha _1 ,\beta ) \le \log 3.$

Рассмотрим теперь сложный опыт $А_{k}=\alpha _{1}\alpha _{2}$... $\alpha _{k}$, заключающийся в $k$ последовательных взвешиваниях, он дает информацию, не превосходящую $k\cdot log3$. Если опыт $A_{k}$ позволяет полностью определить исход опыта $\beta$, то должно быть $H(A_k ) \ge I(A_k ,\beta ) \ge H(\beta )$ или $k\cdot log3 \ge log18$. Отсюда

$3^k \ge 18\quad \mbox{и} \quad k \ge \log _3 18,$ т.к - целое число, то $k \ge 3$.

Покажем на "кодовом дереве", как с помощью трех взвешиваний определить фальшивую монету. Каждое взвешивание строим таким образом, чтобы на любой возможный исход приходилась максимальная энтропия.

Рис. 83

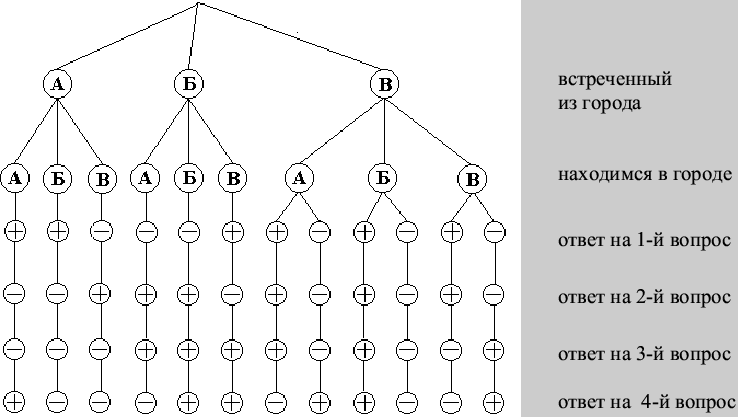
Пример 139. Имеются три города А, Б и В, причем жители А во всех случаях говорят правду, жители Б - только неправду, а жители В через раз отвечают на вопросы верно и неверно. Наблюдатель хочет выяснить, в каком городе он находится и в каком городе живет встреченный им человек. Сколько вопросов ему потребуется задать этому встречному, если на все вопросы его собеседник отвечает "да" или "нет"?

Решение. Поскольку наблюдатель может находиться в одном из трех городов А, Б или В и его собеседник может проживать в любом из этих трех городов, то интересующий нас опыт имеет 9 равновозможных исходов. Следовательно, энтропия $Н(\beta )$ = log 9.${\rm O}$усть опыт $A_k = \alpha _1 \alpha _2 ...\alpha _k$ состоит в том, что наблюдатель задает $k$ вопросов. Так как на каждый вопрос он может получить только два ответа, то $Н(\alpha _{i}) \quad \le 1$ бита.

С другой стороны, по свойству 6) энтропии:

$$H(A_k ) = H(\alpha _1 \alpha _2 ...\alpha _k ) \le H(\alpha _1 ) + H(\alpha _2 ) + ... + H(\alpha _k ) \le k$$

и $\log 9 \le I(A_k )^3 \le H(A_k ) \le k$.

Получили, что $k \ge \log 9 > \log 8 = 3$, и четыре удачно поставленных вопроса позволяют выяснить, в каком городе мы находимся и в каком городе живет встреченный человек.

Четыре вопроса могут быть следующие:

Нахожусь ли я в одном из городов А или Б?

Нахожусь ли я в городе В?

Живете ли Вы в городе В?

Нахожусь ли я в городе А?

Покажем на "дереве ответов", что ответы на эти четыре вопроса позволяют однозначно определить, из какого города встреченный человек и в каком городе мы находимся. "Дерево ответов" выглядит следующим образом:

Рис. 84

На следующем примере покажем, что минимальное количество вспомогательных опытов, полученных из анализа условий задачи, не всегда достаточно для выделения интересующего нас объекта.

Пример 140. Жители города А говорят только правду, а жители города Б чередуют правдивые и ложные ответы. Сколько вопросов потребуется задать наблюдателю встречному человеку, чтобы определить, в каком городе он находится и из какого города его собеседник?

Решение. Как и в предыдущем примере, анализ условия задачи приводит нас к следующему выводу, что $k \ge \log 4 = 2$ (бит).

Откуда следует, что потребуется задать не менее двух вопросов. Сформулируем возможные два вопроса:

Нахожусь ли я в городе А?

Нахожусь ли я в городе Б?

В этом случае дерево ответов выглядит следующим образом:

Рис. 85

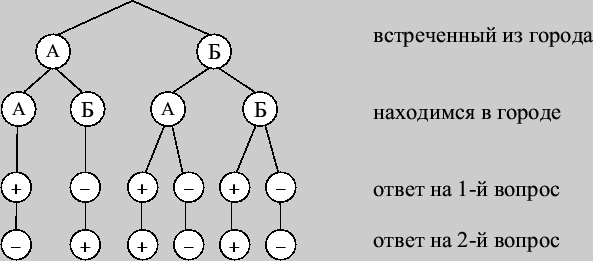
Поскольку по возможным ответам нельзя однозначно определить, где находится наблюдатель и откуда встреченный им человек, то потребуется задать еще один вопрос, например, "$2\times 2 = 4$?".

Вопросы для самоконтроля

1. Какие вы знаете типы логических задач, которые допускают для их решения использование понятия информации?

2. Условия применимости информации для определения объекта.

3. Как находить наименьшее число опытов при анализе занимательных логических задач?

4. Какое утверждение об энтропии используется часто при решении логических задач?

5. Решение простейших логических задач с использованием энтропии и двоичной системы счисления.

6. Иллюстрация решения логических задач на "кодовом дереве".

Задачи

I 271. 50 студентов-математиков III курса загадали одного из студентов. Сколько вопросов надо задать курсу, чтобы отгадать выбранного студента, если курс на все вопросы отвечает лишь "да" или "нет"?

272. Вы хотите узнать номер телефона жителя Ярославля, задавая вопросы, на которые он отвечает либо "да", либо "нет". За какое возможно меньшее количество вопросов вам это удастся?

273. Сколько вопросов надо задать, чтобы отгадать день рождения незнакомого человека, если на все вопросы он будет отвечать "да" или "нет"?

274. Имеется 9 монет одного достоинства, одна из которых фальшивая и легче других. Как на чашечных весах без гирь обнаружить фальшивую монету?

275. Известно, что жители одного города всегда говорят правду, а другого всегда обманывают. Каково наименьшее число вопросов должен задать наблюдатель, чтобы определить, в каком городе живет встреченный им человек и в каком городе он находится?

276. Имеется 12 монет одного достоинства, одна из которых фальшивая и тяжелее других. Сколькими взвешиваниями на чашечных весах без гирь можно обнаружить эту фальшивую монету?

II 277. Имеется 27 монет одного достоинства, среди которых одна фальшивая, отличающаяся от остальных по весу. Сколькими взвешиваниями на чашечных весах и как можно обнаружить эту фальшивую монету?

278. Известно, что жители города А всегда говорят правду, а жители города В - один раз правду, а другой раз - ложь. Какое наименьшее число вопросов и каких может задать наблюдатель, чтобы определить город, в котором он находится, и в каком городе живет его собеседник?

III 279. Вы хотите узнать шестизначный номер моего телефона, задавая вопросы, на которые я отвечаю либо "да", либо "нет", и на один из ваших вопросов я могу дать неправильный ответ. Какое наименьшее число вопросов и какие вы будете задавать, чтобы отгадать номер?

280. Из пяти имеющихся предметов никакие два не весят одинаково. Расположите эти предметы в ряд по возрастанию их веса, используя рычажные весы без гирь. Каково наименьшее число взвешиваний?

Далее: §27. Кодирование и декодирование Вверх: Глава IV. Энтропия и Назад: §27. Количество информации