Основные задачи, которые ставил перед собой К. Шеннон в середине ХХ в. при создании направления, в последующие годы получившего название "теория информации", были связаны с чисто техническими вопросами электросвязи и радиосвязи. Работы Шеннона оказали большое стимулирующее влияние на исследования, относящиеся к передаче и сохранению какой бы то ни было информации в природе и технике.
Информацию можно измерить числом, которое называется количеством информации
об опыте ![]() , содержащемся в опыте
, содержащемся в опыте ![]() :
:
Количество информации ![]() ,
,
![]() оказывает, насколько
осуществление опыта
оказывает, насколько
осуществление опыта ![]() уменьшает неопределенность опыта
уменьшает неопределенность опыта ![]() .
.
Количество информации предлагается находить на ориентированном графе:
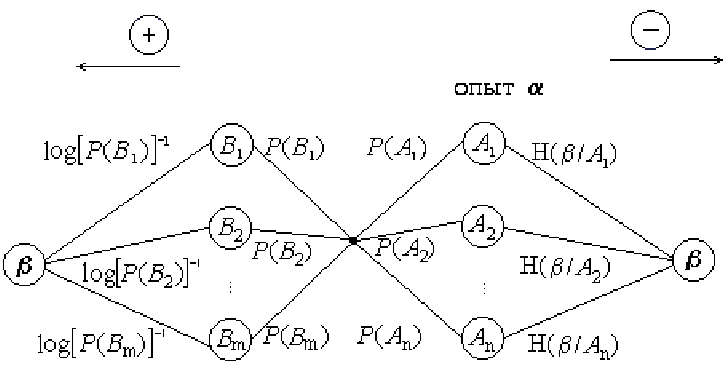
Поскольку представленный способ вычисления количества информации на графе является авторским, то проиллюстрируем его на следующем примере.
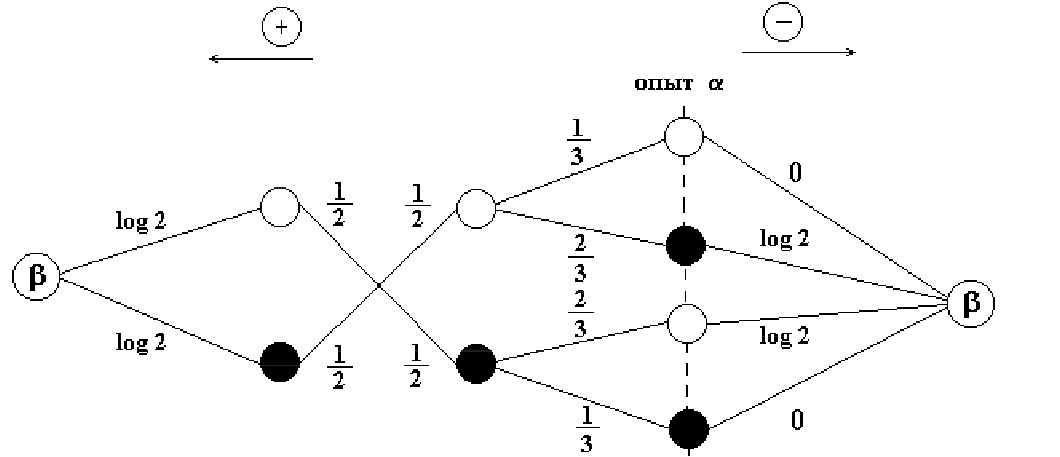
Пример 131. В урне два белых и два черных шара. Опыт ![]() состоит в извлечении из урны шара, а опыт
состоит в извлечении из урны шара, а опыт ![]() - в предварительном
извлечении из той же урны (без возвращения) двух шаров. Найти количество
информации об опыте
- в предварительном
извлечении из той же урны (без возвращения) двух шаров. Найти количество
информации об опыте ![]() , содержащемся в опыте
, содержащемся в опыте ![]() .
.
Решение. Построим ориентированный граф опытов ![]() и
и ![]() .
.
Свойства количества информации:
К понятию меры количества информации можно подойти с другой стороны. Пусть
происходит некоторое событие ![]() с вероятностью
с вероятностью ![]() . Если вероятность
. Если вероятность ![]() близка
к единице, то событие
близка
к единице, то событие ![]() практически достоверно и его появление не несет
никакой информации. Однако если произойдет противоположное событие
практически достоверно и его появление не несет
никакой информации. Однако если произойдет противоположное событие ![]() , то
, то ![]() несет значительную информацию (близкую к сенсации).
Поэтому за количество меры информации события
несет значительную информацию (близкую к сенсации).
Поэтому за количество меры информации события ![]() принимаем величину
принимаем величину
Пусть ![]() есть некоторый эксперимент с исходами
есть некоторый эксперимент с исходами ![]() ,
, ![]() , ...
,
, ...
, ![]() , которые осуществляются с вероятностями
, которые осуществляются с вероятностями ![]() ,
, ![]() (
( ![]() , ...
,
, ...
, ![]() . Информация, полученная в результате испытания
. Информация, полученная в результате испытания ![]() , есть
случайная величина
, есть
случайная величина ![]() , принимающая значения
, принимающая значения
![]()
![]() .
.
Подсчитаем среднюю информацию опыта ![]() . Примем за меру исхода
. Примем за меру исхода
![]() его вероятность
его вероятность ![]() . Тогда
. Тогда
![\begin{displaymath}
M[I_A ] = - \sum\limits_{i = 1}^n {P(A_i )\log P(A_i ) = H(\alpha ).}
\end{displaymath}](img1227.png)
Таким образом, математическое ожидание информации эксперимента ![]() есть энтропия этого эксперимента.
есть энтропия этого эксперимента.
Единица измерения информации такая, как и энтропии, - 1 бит.
Пример 132. В предыдущем примере поменяем местами очередность
проведения опытов ![]() и
и ![]() . Найти количество информации об опыте
. Найти количество информации об опыте
![]() , содержащемся в опыте
, содержащемся в опыте ![]() .
.
Решение.
Найдем условную энтропию
![]() по графу
по графу
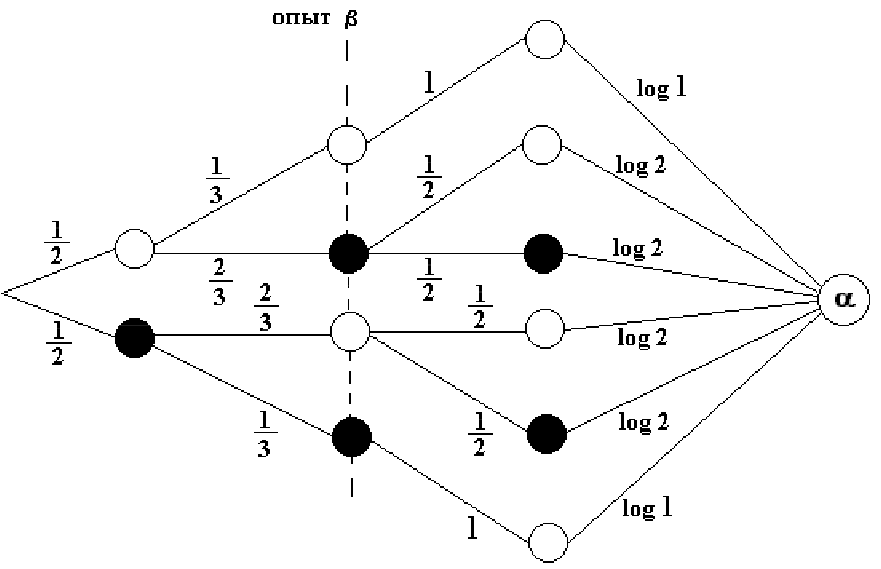
Отсюда
![]()
Эти два примера иллюстрируют свойство 3) количества информации.
Пример 133. Какое количество информации получаем для геометрического распределения, если дополнительно сообщается, что испытаний проводится не больше двух?
Решение.
![]()
Пусть ![]() - проведение двух повторных испытаний, тогда
- проведение двух повторных испытаний, тогда
![\begin{displaymath}
\begin{array}{l}
I(\alpha ,X) = H(X) - H(X / \alpha ) = - \...
...ystyle 1\over\displaystyle p}} \right)\log q]. \\
\end{array}\end{displaymath}](img1235.png)
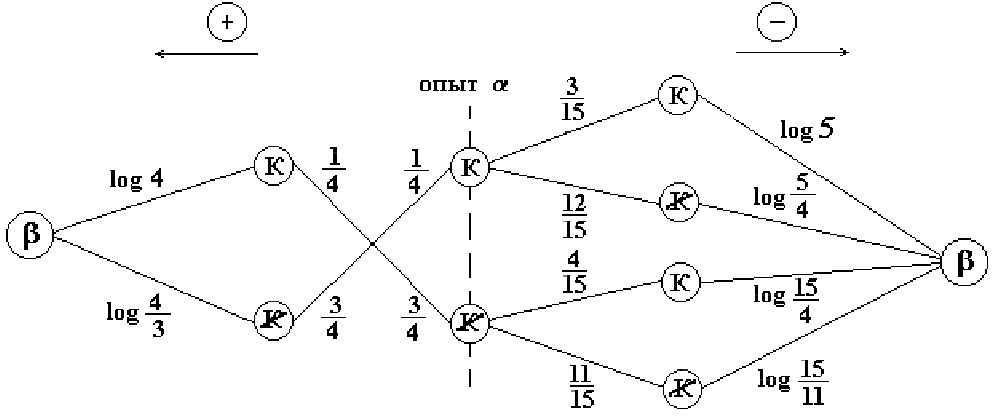
Пример 134. Найти количество информации при вынимании козырной карты из 16 карт с картинками, содержащейся в предварительно извлеченной одной карте.
Решение. Пусть опыт ![]() = {извлечение карты из 16 карт с
картинками}, а опыт
= {извлечение карты из 16 карт с
картинками}, а опыт ![]() = {предварительное извлечение одной
карты}. Для вычисления
= {предварительное извлечение одной
карты}. Для вычисления ![]() ,
,
![]() спользуем
ориентированный граф.
спользуем
ориентированный граф.
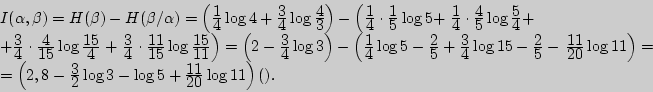
Пример 135. Доказать, что
а)
![]()
б)
![]()
Решение. Поскольку энтропия произведения двух опытов
![]() то
то
С другой стороны,
![]() тогда
тогда
Вопросы для самоконтроля
1. Что такое информация?
2. Как можно измерить информацию?
3. Единицы измерения информации.
4. Возможные способы подсчета информации.
5. Какой информации больше: об опыте ![]() , содержащейся в опыте
, содержащейся в опыте ![]() , или об опыте
, или об опыте ![]() , содержащейся в
, содержащейся в ![]() ?
?
6. Наименьшее значение количества информации и его интерпретация.
7. В каком случае получаем наибольшую информацию?
8. Интерпретация информации через энтропию.
Задачи
I 261. В урне находятся один белый и два черных шара. Найдите количество информации об извлечении шара, содержащейся в предварительном извлечении одного шара.
262. Найдите количество информации при вынимании козырной карты из колоды в 52 карты, содержащейся в предварительно извлеченной одной карте.
263. Найдите количество информации о простых цифрах при извлечении двух карточек из цифровой азбуки, содержащейся в предварительном извлечении одной карточки.
264. В каком отношении находятся известные единицы измерения инфор-мации: двоичная (бит), натуральная (нат), десятичная (дит)?
265. Какое количество информации следует получить, чтобы определить студента, выбранного из 48 "математиков" III курса?
266. Какое количество информации в среднем получает человек, опреде-ляющий день рождения своего собеседника, когда последний сообщает ему месяц, в котором он родился?
II 267. Из урны, содержащей два белых и три черных шара, извлекли шар. Найдите информацию об этом опыте, содержащуюся в предварительном извлечении из этой урны пары шаров.
268. Предлагается угадать карту, наудачу вынутую из колоды в 36 карт. Какое количество информации получит угадывающий, если дополни-тельно сообщить:
а) масть вынутой карты,
б) что вынутая карта оказалась тузом?
III 269. Какое количество информации получаем для биноминального распределения, если известно, что повторные испытания проводятся ровно два раза?
270. Какое количество информации получаем для геометрического распре-деления, если дополнительно сообщается, что испытаний проводится не больше трех?