Далее: §27. Количество информации Вверх: Глава IV. Энтропия и Назад: §25. Энтропия случайных величин

§26. Энтропия цепей Маркова

Энтропию цепей Маркова с вектором начальных вероятностей $\vec а (P(E_{1}) P(E_{2}) \ldots , P(E_{n}))$ находим как математическое ожидание условных энтропий системы $E$ относительно всех ее состояний:

$$H(E) = P(E_1 ) \cdot H(E / E_1 ) + P(E_2 ) \cdot H(E / E_2 ) + ... + P(E_n ) \cdot H(E / E_n ),$$

где $H(E / E_m ) = p_{m1} \log p_{m1}^{ - 1} + p_{m2} \log p_{m2}^{ - 1} + ... + p_{mn} \log p_{mn}^{ - 1} .$

Нахождение энтропии цепи Маркова с вектором начальных вероятностей допускает удобную интерпретацию на графе:

Рис. 77

$$H(E) = \sum\limits_i {P(E_i ) \cdot H(E / E_i )}$$

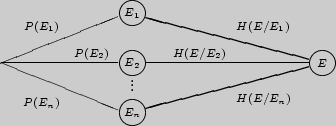
Энтропию цепей Маркова предлагаем находить, суммируя условные энтропии системы $E$ относительно всех ее состояний.

Пример 126. Найти энтропию цепи Маркова E, заданной матрицей перехода

$${\rm {\bf P}} = \left[ {\begin{array}{l} 0,2 \\ 0,7 \\ ... ...ft. {\begin{array}{l} 0,8 \\ 0,3 \\ \end{array}} \right].$$

Решение. $H(E) = H(E / E_1 ) + H(E / E_2 ),$ где $Н(E / E_1 ) = {\displaystyle 1\over\displaystyle 5}\log 5 + {\displaystyle 4\over\displaystyle 5}\log {\displaystyle 5\over\displaystyle 4},$ а $Н(E / E_2 ) = {\displaystyle 7\over\displaystyle 10}\log {\displaystyle 10\over... ...isplaystyle 3\over\displaystyle 10}\log {\displaystyle 10\over\displaystyle 3}.$

Следовательно, $Н(E) = (\log 5 - {\displaystyle 4\over\displaystyle 5} \cdot 2) + (\log 10 - 0,7\log 7 - 0,3\log 3) = \quad = 2\log 5 - 0,6 - 0,7\log 7 - 0,3\log 3$ (бит).

Пример 127. На сколько изменится энтропия цепи Маркова из предыдущего примера, если допустить переход за два шага?

Решение. Цепь Маркова $E_{1}$ за два шага задается квадратом матрицы P.

$${\rm {\bf P}}^{\rm {\bf 2}} = \left[ {\begin{array}{l} 0,2 ... ...{array}{l} {\rm0,4} \\ {\rm0,65} \\ \end{array}} \right].$$

Тогда $H(E_1 ) = \left( {{\displaystyle 3\over\displaystyle 5}\log {\displaystyle 5\ov... ...\over\displaystyle 5}\log 3 - {\displaystyle 2\over\displaystyle 5}} \right) +$

$+ \left( {\log 5 + 2 - {\displaystyle 7\over\displaystyle 20}\log 7 - {\displa... ...tyle 20}\log 13} \right) = 2\log 5 + 1,6 - 0,6\log 3 - 0,35\log 7 - 0,65\log 13$(бит) и $H(E_1 ) - H(E) = 2,2 - 0,3\log 3 + 0,35\log 7 - 0,65\log 13 \approx 0,3$(бит).

Таким образом, энтропия возросла на 0,3 бита.

Пример 128. Найти энтропию цепи Маркова, заданной матрицей вероятностей перехода

$$\mbox{\textbf{P}} = \left[ {\begin{array}{l} 0,2 \\ 0,5 \... ... \\ {\rm0,2 0,3} \\ {\rm0,1 0,3} \\ \end{array}} \right]$$

и вектором начальных вероятностей $\vec {а}$(0,6; 0,1; 0,3).

Решение. Находим $H(E)$ как вес графа:

Рис. 78

$$H(E / E_1 ) = {\displaystyle 2\over\displaystyle 10}\log {\d... ...laystyle 2}\log 2 = 0,5\log 5 - 0,3\log 3 + 0,8 = H(E / E_2 ),$$

$$H(E / E_3 ) = {\displaystyle 6\over\displaystyle 10}\log {\d... ...splaystyle 10\over\displaystyle 3} = \log 5 - 0,9\log 3 + 0,4.$$

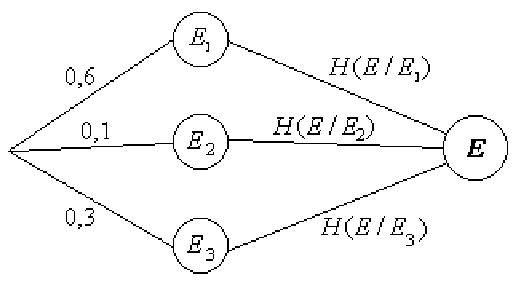
$H(E) = 0,7(0,5\log 5 - 0,3\log 3 + 0,8) + 0,3(\log 5 - 0,9\log 3 + 0,4) = = 0,65\log 5 - 0,48\log 3 + 0,68$(бит).

Пример 129. Игральная кость под воздействием ветра с вероятностью $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ остается на месте, с вероятностью $\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 6$}$переворачивается на противоположную грань и равновероятно поворачивается на соседние грани. Найти энтропию данной цепи Маркова.

Решение. Рассматриваемую цепь Маркова можно задать следующей матрицей перехода:

$$\mbox{\textbf{Р}} = \left[ {\begin{array}{l} \raise0.5ex\hb... ...m\lower0.25ex\hbox{$\scriptstyle 2$} \\ \end{array}} \right]$$

$H(E) = \left[ {{\displaystyle 1\over\displaystyle 2}\log 2 + \left( {{\displays... ... + {\displaystyle 1\over\displaystyle 6}\log 6} \right] \cdot 6 = (8 + 3\log 3)$(бит).

Пример 130. Найти энтропию цепи Маркова из предыдущего примера, полагая, что в начальный момент времени игральный кубик бросается на ровную поверхность.

Решение. В этом случае имеем цепь Маркова $Е_{1}$ с вектором начальных вероятностей $\vec {а}\left( {{\displaystyle 1\over\displaystyle 6},{\displaystyle 1\over\dis... ...playstyle 1\over\displaystyle 6},{\displaystyle 1\over\displaystyle 6}} \right)$ и $Н(Е_1 ) = {\displaystyle 1\over\displaystyle 6}Н(Е / Е_1 ) + {\displaystyle 1\o... ...e 4\over\displaystyle 3} + {\displaystyle 1\over\displaystyle 2}\log 3} \right)$ (бит).

Вопросы для самоконтроля

1. Что такое энтропия системы относительно одного из ее состояний?

2. В каком случае энтропия системы относительно одного из ее состояний является наибольшей, а в каком - наименьшей?

3. Как определяется энтропия цепей Маркова с вектором начальных вероятностей?

4. Различные подходы к введению энтропии цепей Маркова.

5. В каком случае при увеличении числа состояний системы энтропия не изменяется?

6. Приведите модели цепей Маркова для единицы измерения энтропии.

7. Когда энтропия цепей Маркова принимает наибольшее значение?

8. Приведите примеры цепей Маркова с наибольшими и наименьшими значениями энтропии.

Задачи

I 251. Какую степень неопределенности содержит выбор состояния $E_{1}$ в цепи Маркова, заданной матрицей

$${\mbox{\bf Р}} = \left[ {\begin{array}{l} 1 \mathord{\left/... ...n-\nulldelimiterspace} 2 \\ {\rm0} \\ \end{array}} \right]$$

252. Дана матрица вероятностей перехода

$${\mbox{\bf Р}} = \left[ {\begin{array}{l} 1 \mathord{\left/... ...\right. \kern-\nulldelimiterspace} 8 \\ \end{array}} \right]$$

и вектор начальных вероятностей $\vec {а} = (1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3,2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3).$ Найдите энтропию задан-ной цепи Маркова.

253. Найдите энтропию системы, которая находится в одной из вершин четырехугольника и переходит в соседние вершины с вероятностью $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ , а в противоположную - с вероятностью $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$.

254. Найдите энтропию системы, заданной матрицей вероятностей пере-хода

$$P = \left[ {\begin{array}{l} 0,2{\rm0,3} \\ {\rm0,1 0,5} ... ...{\rm0,5} \\ {\rm0,4} \\ {\rm0,4} \\ \end{array}} \right]$$

и вектором начальных вероятностей $\vec {а} = (0,1; 0,3; 0,6).$

255. Сравните энтропии цепей Маркова, заданных матрицами вероятнос-тей перехода

$${\mbox{\bf Р}} = \left[ {\begin{array}{l} \raise0.5ex\hbox{... .... {\begin{array}{l} 0 \\ 0 \\ 1 \\ \end{array}} \right]$$

256. Цепь Маркова задана вектором начальных вероятностей $\vec {а} =$ (0,5;0,4;0,1) и матрицей вероятностей перехода

$$P = \left[ {\begin{array}{l} 0{\rm0,2} \\ {\rm0,6 0,3} \\... ...\rm0,8} \\ {\rm0,1} \\ {\rm0,5} \\ \end{array}} \right].$$

Найдите энтропию заданной цепи Маркова.

II 257. Даны вектор начальных вероятностей $\vec {а} = (1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspa... ...ce} 3,1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2)$ и переходные вероятности $р_{1i} = {\displaystyle i\over\displaystyle 6},p_{2i} = {\displaystyle 3 + i\over\displaystyle 15},p_{3i} = {\displaystyle 6 + i\over\displaystyle 24}$ ($i$=1, 2, 3). Найдите энтропию цепи Маркова за два шага.

258. Рассмотрим марковскую цепь с двумя состояниями $E_{1}$ и $E_{2}$ и матрицей вероятностей перехода

$${\mbox {\bf Р}} = \left[ {\begin{array}{l} 1 \mathord{\left... ...right. \kern-\nulldelimiterspace} 3 \\ \end{array}} \right].$$

Найдите энтропию цепи Маркова за три шага.

III 259. В двух отделениях ящика находятся три шара. Каждую минуту случайным образом выбирается отделение и из него перекладывается в другое отделение один шар. Найдите энтропию марковской цепи, рассмат-ривающей в качестве состояний число шаров в первом отделении.

260. По двум урнам разложено N черных и N белых шаров так, что каждая урна содержит N шаров. Число белых шаров в первой урне определяет состояние системы. В каждый момент времени выбирают случайно по одному шару из урны и выбранные шары меняют местами. Найдите энтропию заданной цепи Маркова.

Далее: §27. Количество информации Вверх: Глава IV. Энтропия и Назад: §25. Энтропия случайных величин