Энтропия ![]() дискретной случайной величины вычисляется по
формуле
дискретной случайной величины вычисляется по
формуле
Для непрерывной случайной величины ![]() с плотностью вероятности
с плотностью вероятности
![]() определяется дифференциальная энтропия как
определяется дифференциальная энтропия как
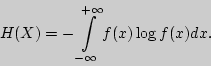
Здесь везде полагаем, что
![]()
Пример 121. Найти энтропию для биномиального распределения.
Решение.
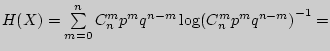
![\begin{displaymath}
= - \sum\limits_{m = 0}^n {C_n^m p^mq^{n - m}\left[ {\log C_n^m + m\log p +
(n - m)\log q} \right]} =
\end{displaymath}](img1142.png)
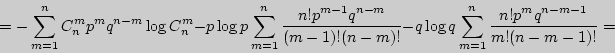
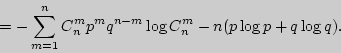
Пример 122. Найти энтропию для геометрического распределения.
Решение. Проводим независимые повторные испытания до появления "успеха". Для вычисления Н(X) воспользуемся графом:
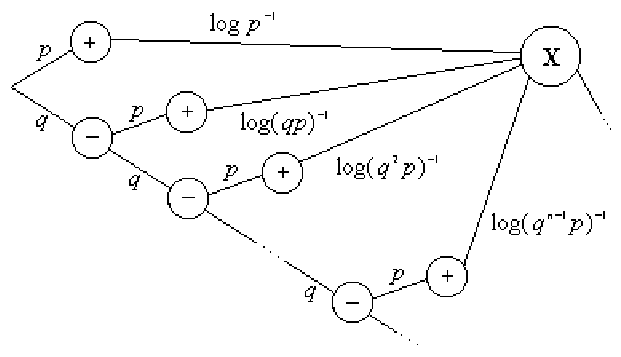
Пример 123. Найти дифференциальную энтропию для показательного распределения.
Решение.
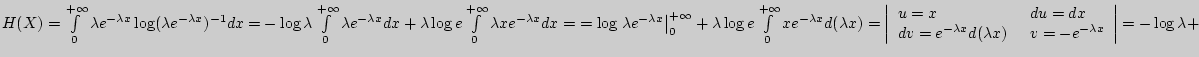
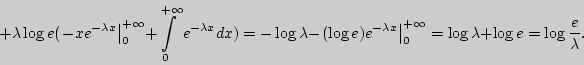
Пример 124. Найти дифференциальную энтропию для нормального закона распределения.
Решение.
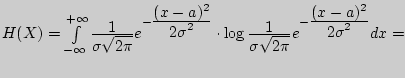
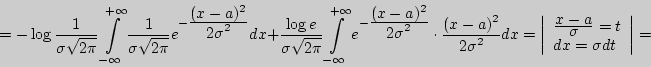
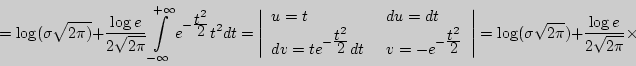
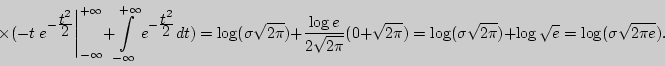
Пример 125. Найти дифференциальную энтропию для случайной величины, распределенной по закону Лапласа.
Решение. Для закона Лапласа
![]() поэтому
поэтому
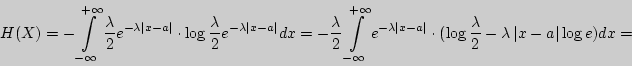
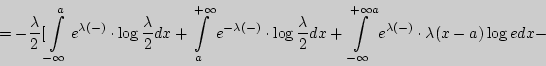
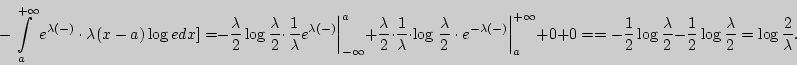
Вопросы для самоконтроля
1. Как определяется энтропия дискретных случайных величин?
2. Приведите примеры вычисления энтропии дискретной случайной вели-чины на графе.
3. Чему равна энтропия индикатора события ![]() ?
?
4. В каком случае энтропия индикатора события ![]() наибольшая?
наибольшая?
5. Приведите примеры энтропий для классических законов распределения.
6. Для каких случайных величин задается дифференциальная энтропия?
7. Чему равна дифференциальная энтропия для показательного закона распределения?
Задачи
I 241. Найдите энтропию для числа белых шаров при извлечении двух шаров из урны, содержащей два белых и один черный шар.
242. Найдите энтропию для числа козырных карт при извлечении двух карт из колоды в 36 карт.
243. Какую степень неопределенности содержит опыт угадывания суммы очков на извлеченной кости из полного набора домино?
244. Найдите энтропию для числа тузов при извлечении трех карт из карт с картинками.
245. Найдите дифференциальную энтропию для равномерного распределе-ния.
246. Найдите дифференциальную энтропию для показательного закона
распределения, если известно, что случайная величина ![]() принимает значение
меньше единицы с вероятностью 0,5.
принимает значение
меньше единицы с вероятностью 0,5.
II 247. Чему равна энтропия для геометрического закона распределения?
248. Найдите дифференциальную энтропию для распределения Коши.
III 249. Найдите энтропию для распределения Пуассона.
250. Найдите дифференциальную энтропию для распределения Лапласа.