Далее: Глава V. Математическая статистика Вверх: Глава IV. Энтропия и Назад: §30. Блочные коды

§29. Коды Фано и Хаффмана

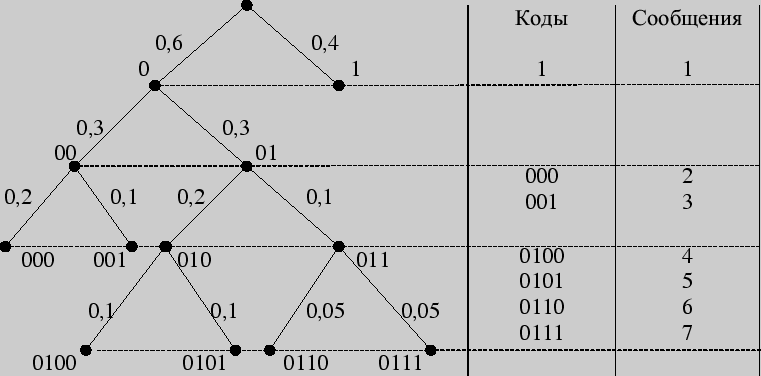
Коды Фано и Хаффмана являются оптимальными и префиксными. При построении искомых кодов будем применять как традиционный табличный способ кодирования, так и использовать "кодовые деревья".

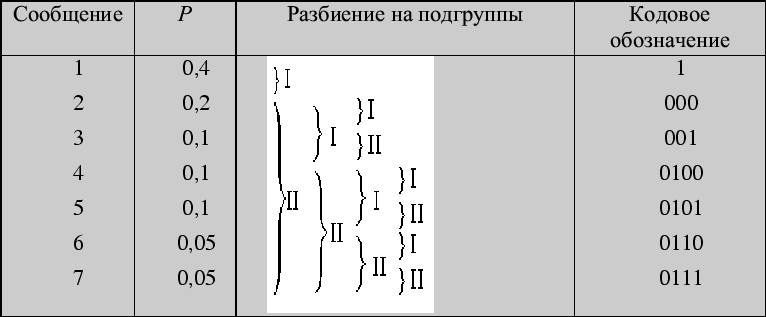
При кодировании по Фано все сообщения записываются в таблицу по степени убывания вероятности и разбиваются на две группы примерно (насколько это возможно) равной вероятности. Соответственно этой процедуре из корня кодового дерева исходят два ребра, которым в качестве весов присваиваются полученные вероятности. Двум образовавшимся вершинам приписывают кодовые символы 0 и 1. Затем каждая из групп вероятностей вновь делится на две подгруппы примерно равной вероятности. В соответствии с этим из каждой вершины 0 и 1 исходят по два ребра с весами, равными вероятностям подгрупп, а вновь образованным вершинам приписывают символы 00 и 01, 10 и 11. В результате многократного повторения процедуры разделения вероятностей и образования вершин приходим к ситуации, когда в качестве веса, приписанного ребру бинарного дерева, выступает вероятность одного из данных сообщений. В этом случае вновь образованная вершина оказывается листом дерева, т.к. процесс деления вероятностей для нее завершен. Задача кодирования считается решенной, когда на всех ветвях кодового бинарного дерева образуются листья.

Пример 151. Закодировать по Фано сообщения, имеющие следующие вероятности:

сообщение	1	2	3	4	5	6	7
вероятность	0,4	0,2	0,1	0,1	0,1	0,05	0,05

Решение 1 (с использованием кодового дерева)

Рис. 91

Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами.

Решение 2 (табличный способ)

Цена кодирования (средняя длина кодового слова $l)$ является критерием степени оптимальности кодирования. Вычислим ее в нашем случае.

$$l = \sum\limits_{i = 1}^7 {l_i \cdot p_i = 1 \cdot 0,4 + 3 \... ... + 3 \cdot 0,1 + 4 \cdot (0,1 \cdot 2 + 0,05 \cdot 2) = 2,5} .$$

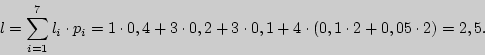
Для того, чтобы закодировать сообщения по Хаффману, предварительно преобразуется таблица, задающая вероятности сообщений. Исходные данные записываются в столбец, две последние (наименьшие) вероятности в котором складываются, а полученная сумма становится новым элементом таблицы, занимающим соответствующее место в списке убывающих по величине вероятностей. Эта процедура продолжается до тех пор, пока в столбце не останутся всего два элемента.

Пример 152. Закодировать сообщения из предыдущего примера по методу Хаффмана.

Решение 1. Первый шаг

Вторым шагом производим кодирование, "проходя" по таблице справа налево (обычно это проделывается в одной таблице):

Решение 2. Построение кодового дерева начинается с корня. Двум исходящим из него ребрам приписывается в качестве весов вероятности 0,6 и 0,4, стоящие в последнем столбце. Образовавшимся при этом вершинам дерева приписываются кодовые символы 0 и 1. Далее "идем" по таблице справа налево. Поскольку вероятность 0,6 является результатом сложения двух вероятностей 0,4 и 0,2, из вершины 0 исходят два ребра с весами 0,4 и 0,2 соответственно, что приводит к образованию двух новых вершин с кодовыми символами 00 и 01. Процедура продолжается до тех пор, пока в таблице остаются вероятности, получившиеся в результате суммирования. Построение кодового дерева заканчивается образованием семи листьев, соответствующих данным сообщениям с присвоенными им кодами. Дерево, полученное в результате кодирования по Хаффману, имеет следующий вид:

Рис. 92

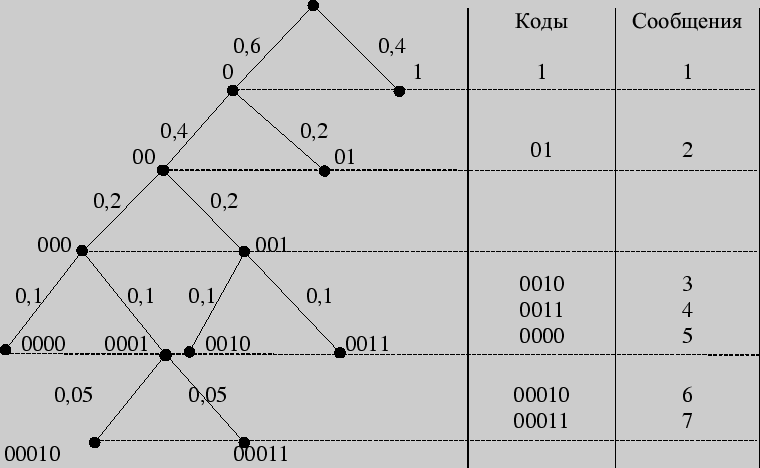
Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами. Таблица кодов имеет вид:

сообщение	1	2	3	4	5	6	7
код	1	01	0010	0011	0000	00010	00011

Цена кодирования здесь будет равна

$$l = \sum\limits_{i = 1}^7 {l_i p_i = 1 \cdot 0,4 + 2 \cdot 0,2} + 4 \cdot (0,1 \cdot 3) + 5 \cdot (0,05 \cdot 2) = 2,5.$$

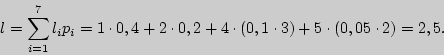
Для передачи данных сообщений можно перейти от побуквенного (поцифрового) кодирования к кодированию "блоков", состоящих из фиксированного числа последовательных "букв".

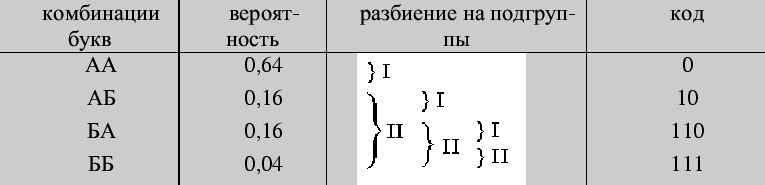
Пример 153. Провести кодирование по методу Фано двухбуквенных комбинаций, когда алфавит состоит из двух букв $А$ и $Б$, имеющих вероятности $Р(А)$ = 0,8 и $Р(Б)$ = 0,2.

Решение.

Цена кода $l = 1 \cdot 0,64 + 2 \cdot 0,16 + 3 \cdot (0,16 + 0,04) = 1,56$, и на одну букву алфавита приходится 0,78 бита информации. При побуквенном кодировании на каждую букву приходится следующее количество информации:

$Н = {\displaystyle 4\over\displaystyle 5}\log {\displaystyle 5\over\displaystyl... ...log 5 - {\displaystyle 4\over\displaystyle 5}\log 4 = \log 5 - 1,6 \approx 0.72$(бит).

Пример 154. Провести кодирование по Хаффману трехбуквенных комбинаций для алфавита из предыдущего примера.

Построим кодовое дерево.

Рис. 93

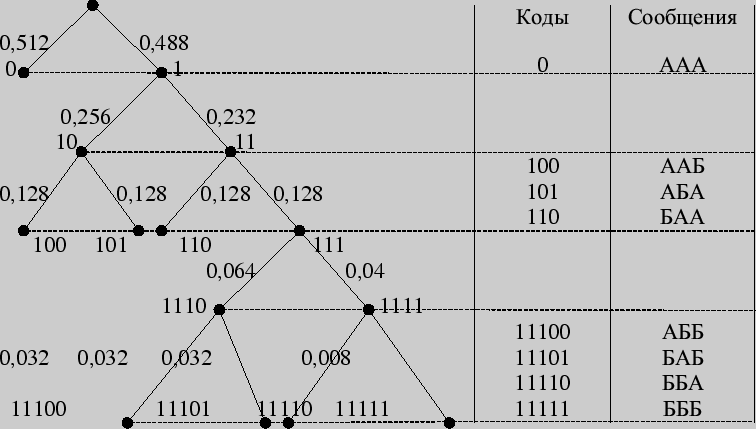
Найдем цену кодирования

$$l = 1 \cdot 0,512 + 3 \cdot (0,128 \cdot 3) + 5 \cdot (0,032 \cdot 3 + 0,008) = 2,184.$$

На каждую букву алфавита приходится в среднем 0,728 бита, в то время как при побуквенном кодировании - 0,72 бита.

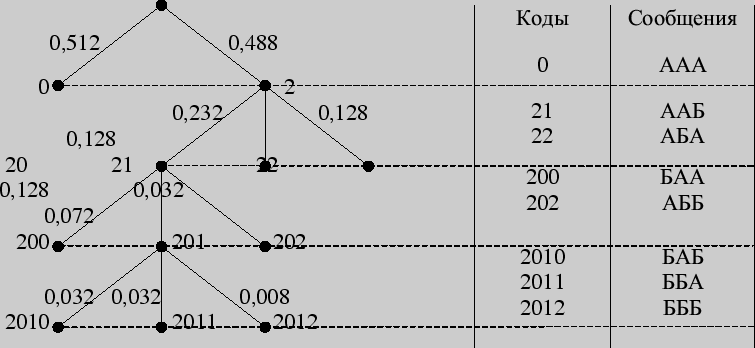
Большей оптимизации кодирования можно достичь еще и использованием трех символов - 0, 1, 2 - вместо двух. Тринарное дерево Хаффмана получается, если суммируются не две наименьшие вероятности, а три, и приписываются каждому левому ребру 0, правому - 2, а серединному - 1.

Пример 155. Построить тринарное дерево Хаффмана для кодирования трехбуквенных комбинаций из примера 153.

Решение. Составим таблицу тройного "сжатия" по методу Хаффмана

Тогда тринарное дерево выглядит следующим образом:

Рис. 94

Вопросы для самоконтроля

1. Как определяется среднее число элементарных сигналов, приходящихся на одну букву алфавита?

2. Префиксные коды.

3. Сколько требуется двоичных знаков для записи кодированного сообщения?

4. На чем основано построение кода Фано?

5. Что такое сжатие алфавита?

6. Какой код самый выгодный?

7. Основная теорема о кодировании.

8. Энтропия конкретных типов сообщений.

Задачи

I 301. Проведите кодирование по методу Фано алфавита из четырех букв, вероятности которых равны 0,4; 0,3; 0,2 и 0,1.

302. Алфавит содержит 7 букв, которые встречаются с вероятностями 0,4; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05. Осуществите кодирование по методу Фано.

303. Алфавит состоит из двух букв, $A$ и $Б$, встречающихся с вероятностями $P(A)$ = 0,8 и $P(Б)$ = 0,2. Примените метод Фано к кодированию всевозмож-ных двухбуквенных и трехбуквенных комбинаций.

304. Проведите кодирование по методу Хаффмана трехбуквенных слов из предыдущей задачи.

305. Проведите кодирование 7 букв из задачи 302 по методу Хаффмана.

306. Проведите кодирование по методам Фано и Хаффмана пяти букв, равновероятно встречающихся.

II 307. Осуществите кодирование двухбуквенных комбинаций четырех букв из задачи 301.

308. Проведите кодирование всевозможных четырехбуквенных слов из задачи 303.

III 309. Сравните эффективность кодов Фано и Хаффмана при кодировании алфавита из десяти букв, которые встречаются с вероятностями 0,3; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05; 0,04; 0,03; 0,03.

310. Сравните эффективность двоичного кода Фано и кода Хаффмана при кодировании алфавита из 16 букв, которые встречаются с вероятностями 0,25; 0,2; 0,1; 0,1; 0,05; 0,04; 0,04; 0,04; 0,03; 0,03; 0,03; 0,03; 0,02; 0,02; 0,01; 0,01.

Далее: Глава V. Математическая статистика Вверх: Глава IV. Энтропия и Назад: §30. Блочные коды