Далее: §38. Критерии Пирсона и Вверх: Глава V. Математическая статистика Назад: §36. Ранговая корреляция

§37. Статистические гипотезы

На разных этапах статистического исследования возникает необходимость в формулировании и экспериментальной проверке некоторых предположительных утверждений (гипотез). Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Выдвигается основная (нулевая) гипотеза $Н_{0}$ и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу $Н_{1}$, которая противоречит нулевой.

В результате статистической проверки гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; вероятность совершить такую ошибку обозначают $\alpha$ и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают $\beta$, а мощностью критерия является вероятность $1- \beta$.

Процедура обоснованного сопоставления высказанной гипотезы с имеющейся выборкой осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотез. Под критической областью понимают совокупность значений критерия, при которых нулевую гипотезу $Н_{0}$ отвергают. Критическую область при заданном уровне значимости следует строить так, чтобы мощность критерия была максимальной.

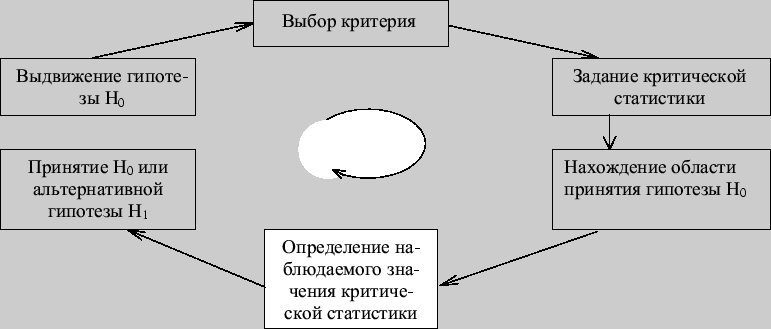
Статистические критерии проверки гипотез разнообразны, но у них единая логическая схема построения, которую представим на рис. 103.

Рис. 103

1. Сравнение двух дисперсий нормальных генеральных совокупностей. При заданном уровне значимости $\alpha$ проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

$$Н_{0}=D[X] = D[Y].$$

В качестве критерия проверки нулевой гипотезы принимают случайную величину отношения большей исправленной дисперсии к меньшей

$$F=S_{б}^{2} \quad / S_{м}^{2}.$$

Величина $F$ имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы $k_{1}=n_{1} - 1$ и $k_{2}=n_{2}- 1$.

Пример 181. Исследование длительности оборотных средств двух групп предприятий (по 13 предприятий в каждой) дало следующие результаты:

$х^{\ast } = 23$ дня, $у^{\ast }= 26$ дней, $\sigma _x^2 = 3$ дня, $\sigma _y^2 = 6$ дней.

Можно ли считать, что отклонения в длительности оборота оборотных средств групп предприятий одинаковы для уровня значимости 0,1?

Решение. В этой задаче надо проверить нулевую гипотезу $Н_{0} : D[X] = D[Y]$ о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе $Н_{1} : D[X] \ne \quad D[Y]$. Используем критерий Фишера-Снедекора со степенями свободы $k_{1}=k_{2} = 13 - 1$ и вычислим наблюдаемое значение критерия (отношение большей дисперсии к меньшей)

$$F_{эмп} = {S_{б}^2 } \mathord{\left/ {\vphantom {{S_{б}^2 } ... .../ {\vphantom {6 3}} \right. \kern-\nulldelimiterspace} 3} = 2.$$

По таблице приложения 6 по уровню значимости для двусторонней критической области $\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-\nulldelimiterspace... ...athord{\left/ {\vphantom {{0,1} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,05$ и числам степеней свободы $k_{1}=k_{2} = 12$ находим критическую точку

$$F_{кр} (0,05; 12; 12) = 2,69.$$

Так как $F_{эмп}= 2 < 2,69 = F_{кр}$, то нет оснований отвергать нулевую гипотезу о равенстве отклонений в длительности оборота оборотных средств двух групп предприятий.

Пример 182. Школьникам давались обычные арифметические задачи, а потом одной случайно выбранной половине учащихся сообщалось, что они не выдержали испытания, а остальным - обратное. Затем у каждого из них спрашивали, сколько секунд ему потребуется для решения новой задачи. Экспериментатор, вычисляя разность между определенным временем решения задачи, которое называл школьник, и результатами ранее выполненного задания, получил следующие данные:

группа 1 (учащиеся, которым сообщалось о положительном результате)	$n_{1} = 13, S_1^2 = 4,06$
группа 2 (учащиеся, которым сообщалось о неудаче)	$n_{2}= 12, S_2^2 = 20,25$

Проверьте на уровне значимости 0,01 гипотезу о том, что дисперсия совокупности детских оценок, имеющих отношение к оценке их возможностей, не зависит от того, что сообщалось детям о плохих результатах испытаний или об удачном решении первой задачи.

Решение. Применим критерий Фишера-Снедекора для нулевой гипотезы $Н_{0} : D[X] = D[Y]$ и конкурирующей $Н_{1} : D[Y] > D[X]$. Вычислим наблюдаемое значение критерия

$$F_{{\rm эмп}} = {S_2^2 } \mathord{\left/ {\vphantom {{S_2^2 ... ...,06}}} \right. \kern-\nulldelimiterspace} {4,06} \approx 4,99.$$

Критическую точку находим в приложении для уровня значимости $\alpha = 0,01$ и числам степеней свободы $k_{1} = 12 - 1$ и $k_{2} = 13 - 1$:

$$F_{кр}(0,01; 11; 12) = 4,22.$$

Получили, что $F_{эмп} = 4,99 > 4,22 = F_{кр}$ и нулевая гипотеза на уровне значимости 0,01 отвергается.

2. Сравнение двух средних нормальных генеральных совокупностей с известными дисперсиями. Проверяется нулевая гипотеза о равенстве генеральных средних рассматриваемых совокупностей с заданными или вычисляемыми дисперсиями. В качестве критерия проверки нулевой гипотезы примем случайную величину

$$Z = {\displaystyle x^\ast - y^\ast \over\displaystyle \sqrt ... ...ft/ {\vphantom {] m}} \right. \kern-\nulldelimiterspace} m} }.$$

Пример 183. Производительность двух моторных заводов, выпускающих дизельные двигатели, характеризуется следующими данными:

1-й завод	72	84	69	74	82	67	75	86	68	61
2-й завод	55	65	73	66	58	71	77	68	68	59

Можно ли считать одинаковыми производительности дизельных двигателей на обоих заводах при уровне значимости $\alpha =0,05$?

Решение. Найдем выборочные числовые характеристики данных независимых выборок:

$$х^{\ast } = 74, D_x^\ast = 59,2, y^{\ast } = 66, D_y^\ast = 43,8.$$

Найдем наблюдаемое значение критерия:

$$Z_{{\rm эмп}} = {\displaystyle x^\ast - y^\ast \over\display... ...e 74 - 66\over\displaystyle \sqrt {5,92 + 4,38} } \approx 2,5.$$

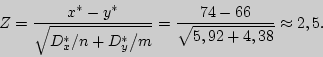
По условию, конкурирующая гипотеза имеет вид $M[X] \ne M[Y]$, поэтому критическая область - двусторонняя.

Найдем критическую точку:

$$\Phi (Z_{{\rm кр}} ) = {(1 - \alpha )} \mathord{\left/ {\vph... ...{(1 - 0,05)} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,475,$$

по таблице функции Лапласа (прил. 2) находим $Z_{кр} \approx 2$.

Так как $\left\vert {Z_{эмп} } \right\vert = 2,5 > 2 = Z_{кр}$, то нулевая гипотеза об одинаковости производительности двух заводов отклоняется.

3. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности. По выборочной средней при заданном уровне значимости проверяется нулевая гипотеза $Н_{0}: a = a_{0}$ о равенстве генеральной средней $a$ гипотетическому значению $a_{0}$. В качестве проверки нулевой гипотезы примем случайную величину

$$U = (\bar {X} - {a_0 )} \mathord{\left/ {\vphantom {{a_0 )} ... ...sqrt n } \sigma }} \right. \kern-\nulldelimiterspace} \sigma ,$$

которая распределена нормально.

Пример 184. Из нормальной генеральной совокупности с известным средним квадратическим отклонением $\sigma = 0,2$ извлечена выборка объема $n = 25$ и по ней найдена выборочная средняя $х^{\ast} = 21,04$. Проверить нулевую гипотезу $Н_{0}: a= a_{0} = 21$, при конкурирующей гипотезе $Н_{1}: а \ne 21$ и уровне значимости 0,1.

Решение. Найдем наблюдаемое значение критерия:

$$U_{{\rm эмп}} = (х^\ast - а_0 ){\sqrt п } \mathord{\left/ {\... ...t {25} } {0,2}}} \right. \kern-\nulldelimiterspace} {0,2} = 1.$$

Найдем критическую точку двусторонней критической области:

$$\Phi (U_{{\rm кр}} ) = (1 - {\alpha )} \mathord{\left/ {\vph... ...hantom {{0,1)} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,45$$

и по таблице функции Лапласа находим $U_{кр} \quad \approx 1,65$.

Поскольку $U_{кр} = 1,65 > 1 = U_{эмп}$, то нулевая гипотеза принимается.

4. Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события. При заданном уровне значимости $\alpha$ проверяется нулевая гипотеза, состоящая в том, что неизвестная вероятность $р$ появления события равна гипотетической вероятности $р_{0}$ серии повторных независимых испытаний.

В качестве критерия проверки нулевой гипотезы принимаем случайную величину

$$U = {\left( {{\displaystyle m\over\displaystyle n} - p_0 } \... ... } }}} \right. \kern-\nulldelimiterspace} {\sqrt {p_0 q_0 } }.$$

Пример 185. По 100 независимым испытаниям найдена относительная частота 0,07. При уровне значимости 0,05 проверить нулевую гипотезу $Н_{0 }: р= р_{0} = 0,1$ при конкурирующей гипотезе $Н_{1 }: р \quad \ne 0,1$.

Решение. Найдем наблюдаемое значение критерия:

$$U_{эмп} = {\displaystyle \left( {m \mathord{\left/ {\vphanto... ...} \over\displaystyle \sqrt {0,07 \cdot 0,93} } \approx - 1,18.$$

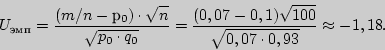
Учитывая, что критическая область двусторонняя, находим $U_{кр}$ из равенства

$$\Phi (U_{кр}) = (1 - {\alpha )} \mathord{\left/ {\vphantom {... ...tom {{0,05)} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,475.$$

По таблице функции Лапласа (прил. 2) находим $U_{кр} \quad \approx 2$.

Поскольку $\left\vert {U_{эмп}} \right\vert = 1,18 < 2 = U_{кр}$, то нет оснований отвергать гипотезу о незначительном отличии наблюдаемой относительной частоты от гипотетической вероятности.

Вопросы для самоконтроля

1. Назовите основные типы статистических критериев проверки гипотез.
2. Что означает уровень значимости критерия?
3. Что общего в методике построения доверительных интервалов и проверки статистических гипотез?
4. Поясните смысл понятий "ошибка первого рода", "ошибка второго рода", "мощность критерия".
5. В чем отличие одностороннего и двухстороннего критериев, простой и сложной гипотез?
6. Как зависят области принятия основной гипотезы от уровня значимости?
7. Как определяются критические границы для одностороннего и двухстороннего критериев при заданном уровне значимости?
8. Приведите примеры практических задач по проверке гипотез о равенстве математических ожиданий, дисперсий.

Задачи

I 361. По двум независимым выборкам, объемы которых $n_{1} = 10$ и $n_{2} = 15$, извлеченным из нормальных генеральных совокупностей $Х$ и $Y$, найдены исправленные выборочные дисперсии $S_{x} = 0,54$ и $S_{y} = 0,32$. При уровне значимости $\alpha = 0,1$ проверьте нулевую гипотезу $Н_{0} : D[Х] = D[Y]$ о равенстве генеральных дисперсий, при конкурирующей гипотезе $Н_{1} : D[X] > D[Y]$.

362. По двум независимым выборкам, объем которых $n_{1} = 9$ и $n_{2} = 16$, извлеченным из нормальных генеральных совокупностей $Х$ и $Y$, найдены выборочные дисперсии $D_x^\ast = 20,2$ и $D_y^\ast = 14$. При уровне значимости $\alpha =0,05$ проверьте нулевую гипотезу $Н_{0} : D[Х] = D[Y]$ о равенстве генеральных дисперсий при конкурирующей гипотезе $Н_{1} : D[X] \ne D[Y]$.

363. Проведено исследование розничного товарооборота продовольственных магазинов в двух районах Ярославской области (по 20 магазинов в каждом). Априори известны средние значения розничного товарооборота - 78,8 и 78,56 тыс. руб. Полученные в результате оценки средних квадратичных отклонений в первом и втором районах соответственно равны 7,2 и 7,8 тыс. руб. Можно ли считать, что разброс розничного товарооборота магазинов в районах неодинаков при уровне значимости $\alpha = 0,1$? Можно ли сделать вывод о разной покупательной способности населения районов?

364. По выборке объема $n_{1} = 30$ найден средний вес $х^{\ast }=130$г. изделий, изготовленных на первом станке; по выборке объема $n_{2} = 40$ найден средний вес $y^{\ast }=125$г. изделий, изготовленных на втором станке. Генеральные дисперсии известны: $D[X] = 60 \mbox{г}^{2}, D[Y] = 80 \mbox{г}^{2}$. Проверьте нулевую гипотезу $Н_{0} : М[Х] = М[Y]$ при конкурирующей гипотезе $М[Х] \ne М[Y]$ и уровне значимости 0,05. Предполагаем, что случайные величины $Х$ и $Y$ распределены нормально и выборки независимы.

365. Исследование пропусков по болезни детей в двух группах детского сада в течение года (по 16 детей в каждой группе) дало следующие результаты: $x^{\ast}= 32$дня, $y^{\ast }= 41$день, $S_x^2 =\mbox{дней}^{2}$, $S_y^2 = 17\mbox{дней}^{2}$.

Можно ли считать, что среднее количество дней пропусков по болезни в обеих группах одинаково при уровне значимости $\alpha = 0,1$?

366. Из нормальной генеральной совокупности с известным средним квадратическим отклонением $\sigma = 10$ известна выборка объема $n = 36$, и по ней найдена выборочная средняя $х^{\ast } = 107,5$. Проверьте нулевую гипотезу $Н_{0} : a = a_{0} = 110$ при конкурирующей гипотезе $Н_{1} : a \ne 110$ и уровне значимости 0,01.

II 367. Из двух партий изделий, изготовленных на двух одинаково настроенных станках, известны малые выборки, объемы которых $n_{1} = 12$ и $n_{2} = 15$. Получены следующие результаты:

Контролируемый размер изделий первого станка	3,4	3,5	3,8	3,9
Число изделий	2	4	5	1

Контролируемый размер изделий второго станка	3,2	3,4	3,7
Число изделий	4	3	8

Проверьте нулевую гипотезу о равенстве средних размеров изделий при уровне значимости 0,05.

368. По 100 независимым испытаниям найдена относительная частота $m/n = 0,15$. При уровне значимости 0,05 проверьте нулевую гипотезу $Н_{0} : р = р_{0} = 0,2$ при конкурирующей гипотезе а) $Н_{1}: р \ne 0,2$; б) $Н_{1} : р < р_{0}$ .

III 369. В банке в течение двух дней проводилось исследование времени обслуживания клиентов, данные которого представлены в таблице:

Номер интервала	Время обслуживания (мин.)	Число клиентов в 1-й день	Число клиентов во 2-й день
1 2 3 4 5 6 7	6-8 8-10 10-12 12-14 14-16 16-18 18-20	2 3 8 12 15 10 3	3 4 9 13 17 8 3

Можно ли считать одинаковыми отклонения от среднего времени обслуживания клиентов банка в 1-й и 2-й дни при $\alpha =0,05$?

370. За смену отказали 20 элементов первого устройства, состоящего из 800 элементов, и 30 элементов второго, состоящего из 1000 элементов. При уровне значимости $\alpha = 0,01$ проверьте нулевую гипотезу $Н_{0} = р_{1} = р_{2} = р$ о равенстве вероятностей отказа элементов обоих устройств при конкурирующей гипотезе $Н_{1} : р_{1} \ne р_{2}$.

Далее: §38. Критерии Пирсона и Вверх: Глава V. Математическая статистика Назад: §36. Ранговая корреляция