Далее: §40. Статистические методы в
Вверх: Глава V. Математическая статистика
Назад: §38. Критерии Пирсона и
Для будущего учителя очень важно уметь анализировать результаты своей
педагогической деятельности, а также грамотно планировать, проводить
психолого-педагогические эксперименты и обрабатывать их результаты, чему и
посвящены остальные два параграфа книги.
Разделение использования методов математической статистики в психологии и
педагогике весьма условно и преследует здесь скорее цель рассмотреть больше
примеров из реальных исследований в этих областях.
Специфика статистической обработки результатов психолого-педагогических
исследований заключается в том, что анализируемая база данных
характеризуется большим количеством показателей различных типов, их высокой
вариативностью под влиянием неконтролируемых случайных явлений,
необходимостью учета объективных и субъективных факторов, сложностью
корреляционных связей между переменными выборками.
Психолого-педагогические исследования можно разбить на три группы. Первая -
это номинальные переменные (пол, возраст и другие анкетные данные и т.д.).
Арифметические операции над такими величинами лишены смысла, так что
результаты описательной статистики (выборочные средние, дисперсия) к таким
величинам не применимы. Классический способ их анализа - разбиение на
классы относительно тех или иных номинальных признаков и проверка значимых
различий по классам. Вторая группа данных имеет количественную шкалу
измерения, но эта шкала является порядковой (ординальной). При анализе
ординальных переменных используются как разбиение на подвыборки, так и
ранговые технологии (например, нахождение ранговой корреляции). Третья
группа - количественные переменные, отражающие степень выраженности
замеряемого показателя, - это успеваемость, тесты Амтхауэра, Кеттелла и
другие оценочные тесты. При работе с выборками этой группы применимы все
стандартные виды анализа, и при достаточно большом объеме выборки их
распределение обычно близко к нормальному.
Одной из главных целей исследования является анализ изменений, происходящих
в процессе обучения, оценка значимости и направленности этих изменений и
выявление основных факторов, влияющих на процесс. При этом возможны два
подхода. Можно рассматривать длительность обучения и вычислять его
корреляцию с интересующими нас индивидуальными характеристиками испытуемого.
Однако проводимые исследования показывают, что в процессе профессионализации
изменяются зачастую не сами показатели, а структура взаимосвязей между ними.
Поэтому более предпочтительным методом является разбиение данных на группы
(подвыборки), их самостоятельный, а затем сравнительный анализ и проверка
значимости различий в группах.
Прежде чем рассматривать конкретные примеры, приведем, следуя [48],
классификацию психолого-педагогических задач и предлагаемых методов их
решений, а также опишем наиболее часто встречающиеся алгоритмы.
Классификация
психологических и педагогических задач и методов их решения
| Задачи |
Условия |
Методы |
| 1. Выявление различий в уровне исследуемого признака |
а) 2 выборки испытуемых |
критерий Розенбаума;
критерий Манна - Уитни;
критерий t Стьюдента |
| |
б) 3 и более выборок испытуемых |
критерий тенденций Джонкира;
критерий Крускала - Уоллиса |
| 2. Оценка сдвига значений исследуемого признака |
а) 2 замера на одной и той же выборке испытуемых |
критерий Вилкоксона;
критерий знаков;
критерий Фишера |
| |
б) 3 и более замеров на одной и той же выборке испытуемых |
критерий Фридмана;
критерий тенденций Пейджа |
| 3. Выявление различий в распределении признака |
а) при сопоставлении эмпирического распределения с теоретическим |
Биноминальный критерий |
| |
|
критерий Пирсона;
критерий Колмогорова - Смирнова |
| |
б) при сопоставлении двух эмпирических признаков |
критерий Фишера |
| 4. Выявление степени согласованности изменений |
а) двух признаков
б) двух иерархий или профилей |
коэффициент ранговой корреляции Спирмена или Кендалла;
критерий линейной корреляции Пирсона |
| 5. Анализ изменений признака под влиянием контролируемых условий |
а) под влиянием одного фактора |
критерий тенденций Пейджа;
однофакторный дисперсный анализ;
критерий Барлетта;
G - критерий Кохрена |
| |
б) под влиянием нескольких факторов одновременно |
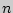 - факторный дисперсный анализ - факторный дисперсный анализ |
Алгоритм
применения критерия U Манна - Уитни
для оценки различий между двумя малыми выборками
по уровню признака
- Перенести все данные испытуемых на индивидуальные карточки, пометив карточки
1-й выборки одним цветом, а 2-й - другим.
- Разложить все карточки в единый ряд по степени возрастания признака и
проранжировать в таком порядке.
- Вновь разложить карточки по цвету на две группы.
- Подсчитать сумму рангов отдельно по группам и проверить, совпадает ли общая
сумма рангов с расчетной.
- Определить большую из двух ранговых сумм
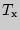 .
.
- Вычислить значение
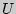 :
:
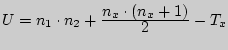 ,
где
,
где 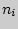 -
количество испытуемых в
-
количество испытуемых в 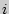 - выборке
- выборке 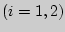 ,
, 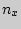 - количество испытуемых в группе с большей суммой рангов.
- количество испытуемых в группе с большей суммой рангов.
- Определить критическое значение
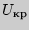 (по таблице прил. 7). Если
(по таблице прил. 7). Если
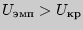 , то
, то 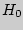 принимается.
принимается.
Пример 191. Индивидуальные значения невербального интеллекта в
выборках студентов специальности история и иностранный язык (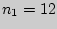 ) и
история и психология (
) и
история и психология (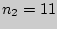 ) приведены в таблице. Подсчитаем ранговые
суммы по выборкам студентов исторического факультета.
) приведены в таблице. Подсчитаем ранговые
суммы по выборкам студентов исторического факультета.
Студенты спец. история и ин. язык
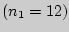 |
Студенты спец. история и психол.
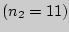 |
| Показатель верб. интеллекта |
Ранг |
Показатель верб. интеллекта |
Ранг |
| 127
116
115
115
111
107
107
107
106
104
95
90 |
23
19
17,5
17,5
12,5
8,5
8,5
8,5
6
3,5
2
1 |
123
122
117
114
113
112
111
108
107
105
104
|
22
21
20
16
15
14
12,5
11
8,5
5
3,5 |
| суммы |
|
127,5 |
|
148,5 |
| средние |
|
|
|
|
Общая сумма рангов:
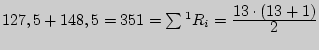
По табл. находим 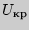 для
для 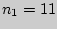 и
и 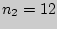
Ответ: гипотеза 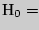 {студенты группы история и психология не
превосходят студентов группы история и ин. язык по уровню невербального
интеллекта} принимается.
{студенты группы история и психология не
превосходят студентов группы история и ин. язык по уровню невербального
интеллекта} принимается.
Алгоритм
применения критерия Т Вилкоксона
для сопоставления двух показателей испытуемых
- Составить список испытуемых.
- Вычислить разность между индивидуальными значениями во 2-м и 1-м замерах
("после" - "до"). Определить, что будет считаться "типичным" сдвигом,
и сформулировать гипотезу.
- Найти абсолютные величины разностей.
- Проранжировать абсолютные величины разностей, начиная с меньшего значения.
- Отметить ранги, соответствующие сдвигам в "нетипичном" направлении,
подсчитать сумму этих рангов
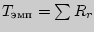 .
.
- Определить критические значения
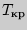 для данного
для данного 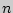 (по таблице
прил. 10). Если
(по таблице
прил. 10). Если
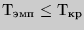 , то сдвиг в "типичную"
сторону по интенсивности достоверно преобладает.
, то сдвиг в "типичную"
сторону по интенсивности достоверно преобладает.
- Критерий применяется для сопоставления показателей, измеренных в двух разных
условиях на одной и той же выборке испытуемых.
Пример 192. 12 участников тренинга партнерского общения дважды
("до" и "после") оценивали у себя уровень владения аргументацией.
Получены данные по 10-балльной шкале.
| № |
1-е измерение
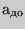 |
2-е измерение
 |
Разность
 |
 |
Ранг абс. разности |
| 1
2
3
4
5
6
7
8
9
10
11
12 |
5
4
5
5
4
3
2
3
5
5
3
4 |
7
5
6
4
5
6
5
5
3
6
3
5 |
2
1
1
-1
1
3
3
2
-2
1
0
1 |
2
1
1
1
1
3
3
2
2
1
0
1 |
9
4,5
4,5
4,5
4,5
11,5
11,5
9
9
4,5
1
4,5 |
| Сумма |
78 |
5.
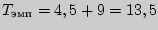
6.
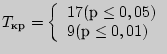

Рис. 104
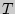 попадает в зону неопределенности, следовательно,
попадает в зону неопределенности, следовательно,
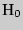 отвергается.
отвергается.
Алгоритм
применения критерия тенденций L Пейджа
для сопоставления трех и более показателей испытуемых
- Проранжировать индивидуальные значения каждого испытуемого, полученные ими в
1-м, 2-м, 3-м и т.д. замерах.
- Просуммировать ранги по условиям, в которых осуществлялись замеры. Проверить
совпадение общей суммы рангов с расчетной.
- Расположить все условия в порядке возрастания их ранговых сумм в таблицах.
- Определить эмпирическое значение
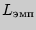 по формуле
по формуле
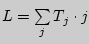 , где
, где 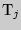 - сумма рангов по
данному условию;
- сумма рангов по
данному условию; 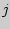 - порядковый номер, приписанный в
упорядоченной последовательности условий.
- порядковый номер, приписанный в
упорядоченной последовательности условий.
- По таблице приложения 8 определить критические значения
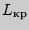 для данного количества испытуемых
для данного количества испытуемых 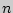 и данного количества условий
и данного количества условий
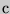 .
.
- Если
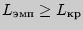 , то тенденция принимается.
, то тенденция принимается.
Пример 193. Установлено, что испытуемые по-разному относятся к
наказаниям, которые совершают по отношению к их детям разные люди.
Определить тенденцию согласия о допустимости телесных наказаний по
результатам оценки степени согласия в психогенном эксперименте, в котором
получены следующие результаты:
| Испытуемые |
Условие
1: "Я сам наказываю" / ранг |
Условие 2: "Бабушка наказывает" /
ранг |
Условие 3: "Учительница наказывает" / ранг |
| 1
2
3
4
5
6
7
8
9
10
11
12 |
4 / 1
5 / 1
1 / 2
3 / 1,5
4 / 2
6 / 1
5 / 1
6 / 1,5
3 / 1,5
2 / 2
7 / 1
5 / 1,5 |
2 / 2
4 / 2,5
1 / 2
3 / 1,5
5 / 1
5 / 2
3 / 2
6 / 1,5
3 / 1,5
2 / 2
5 / 2
5 / 1,5 |
1 / 3
4 / 2,5
1 / 2
2 / 3
1 / 3
3 / 3
4 / 3
4 / 3
1 / 3
2 / 2
4 / 3
3 / 3 |
| Сумма рангов |
I 17 |
II 21,5 |
III 33,5 |
Решение. Проранжируем индивидуальные ранги каждого испытуемого по 3
условиям и запишем их в правые три колонки таблицы, а суммы рангов запишем в
нижней строке. Проверим, что общая сумма рангов
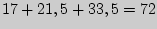 совпадает с расчетной
совпадает с расчетной
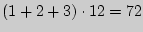 .
.
Определим эмпирическое значение критерия:
Найдем в приложении 8 критическое значение 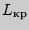 для
для  испытуемых, количества условий
испытуемых, количества условий  и уровня значимости
и уровня значимости
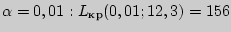 . Поскольку
. Поскольку
 , то высказанная тенденция
отклоняется.
, то высказанная тенденция
отклоняется.
Алгоритм
применения критерия 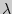 Колмогорова - Смирнова
для сопоставления эмпирического и теоретического
(другого эмпирического) распределений
Колмогорова - Смирнова
для сопоставления эмпирического и теоретического
(другого эмпирического) распределений
- Записать в таблицу наименование разрядов и полученные
эмпирические частоты в два столбца.
- Подсчитать эмпирические относительные частоты
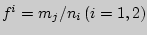 и занести их в 3 и 4-й столбцы.
и занести их в 3 и 4-й столбцы.
- Подсчитать накопленные эмпирические относительные частоты:
Полученные суммы записать в 5-й и 6-й столбцы.
- Записать в 7-й столбец абсолютные величины разностей
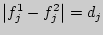 .
.
- Определить
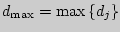 .
.
- Подсчитать значения критерия
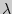 по формуле
по формуле
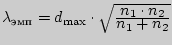 .
.
- По таблице определить, какому уровню статистической значимости
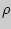 соответствует
соответствует
 .
.
Если
 или
или
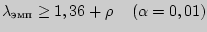 , то различия между распределениями
существенны на соответствующем уровне значимости.
, то различия между распределениями
существенны на соответствующем уровне значимости.
Пример 194. В проективной методике Х. Хекхаузена испытуемому
последовательно предъявляются 6 картин. Всякий раз он сначала рассматривает
картину в течение 20 секунд, а затем в течение 5 минут пишет по ней рассказ.
При обследовании 113 студентов были получены эмпирические распределения
словесных формулировок, отражающих мотивы "надежда на успех" и "боязнь
неудачи", которые приведены в таблице.
| Название
картины |
Кол-во вербальных реакций, отражающих
"надежду" |
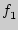 |
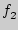 |
Накопленный эмпирический опыт, частота |
Разность абс. |
| |
"надежда на успех" |
"боязнь неудачи" |
|
|
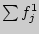 |
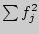 |
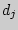 |
| 1. "Мастер измеряет деталь" |
106 |
138 |
0,183 |
0,267 |
0,183 |
0,267 |
0,084 |
| 2. "Преподаватель и ученик" |
102 |
180 |
0,176 |
0,349 |
0,359 |
0,616 |
0,257 |
| 3. "В цехе у машины" |
108 |
34 |
0,186 |
0,066 |
0,545 |
0,682 |
0,137 |
| 4. "У двери директора" |
50 |
87 |
0,086 |
0,169 |
0,631 |
0,851 |
0,22 |
| 5. "Человек в бюро" |
99 |
57 |
0,171 |
0,11 |
0,802 |
0,961 |
0,159 |
| 6. "Улыбающийся юноша" |
115 |
20 |
0,198 |
0,039 |
1,000 |
1,000 |
0 |
| Всего |
580 |
516 |
1,0 |
1,0 |
|
|
|
Можно ли утверждать, что рассматриваемые картины обладают разной побуждающей
силой в отношении мотивов: а) "надежда на успех"; б) "боязнь неудачи"?
5.
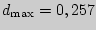 приходится на 2-ю картину.
приходится на 2-ю картину.
6.

7. По таблице определяем уровень статистической значимости
полученного значения 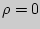 .
.
Пример 195. Найдите корреляционную матрицу по результатам
исследования познавательных особенностей родителей детей с задержкой
психического развития, количественные результаты которого в процентах
представлены в таблице.
| Познавательные
процессы |
Среднее значение результатов детей
Х |
Среднее
значение результатов матерей
Y |
Среднее значение результатов отцов
Z |
| Показатели концентрации внимания |
40,6 |
40,0 |
50,7 |
| Показатели опосредованно-непосредственного запоминания |
45,9 |
48,3 |
47,4 |
| Показатели непроизвольно-произвольного запоминания |
47,3 |
46,7 |
49,1 |
| Показатели уровня логичности мышления |
47,7 |
49,2 |
51,6 |
| Показатели уровня обобщения мышления |
44,5 |
45,7 |
48,1 |
Решение. 1). Найдем выборочные средние для значений результатов детей,
матерей и отцов
2). Найдем выборочные средние квадратические отклонения
Аналогично находим
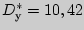 и
и
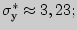
3). Вычислим выборочные ковариации
4). Найдем выборочные коэффициенты корреляции и запишем их в корреляционную
матрицу
Вопросы для самоконтроля
- Какие психологические явления являются измеряемыми? Примеры.
- Принципы классификации шкал измерения.
- Как получить процентальную шкалу?
- Наиболее практически важные параметры распределения признака.
- Как осуществить проверку гипотезы?
- Какие параметрические критерии вы знаете?
- По чему судят о мощности критерия?
- Приведите примеры методов решения психологических задач.
Задачи
I 381. У предполагаемых участников психологического эксперимента
был измерен уровень вербального и невербального интеллекта с помощью
методики Д. Векслера. Были обследованы 12 студентов специальности история и
иностранный язык и 11 студентов специальности история и психология.
Показатели вербального интеллекта представлены в таблице:
| Специальность история и иностранный
язык |
Специальность история и психология |
| Код имени испытуемого |
Показатель вербального интеллекта |
Код имени испытуемого |
Показатель вербального интеллекта |
| 1. В. А.
2. С. А.
3. К. В.
4. П. В.
5.
А. С.
6. Т. А.
7. Ф. А.
8. В. И.
9. К. А.
10. Л. Б.
11. Ф. В.
12. О. А. |
132
134
124
135
132
131
121
127
136
129
136
136 |
1. Т. Н.
2. В. О.
3. В. Е.
4. А. М.
5. З. А.
6. Н. И.
7. К. М.
8. О. К.
9. М. В.
10. Н. М.
11/ В. Н.
|
126
127
132
120
119
126
120
123
120
116
115 |
Используя критерий 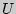 Манна-Уитни, определите, превосходят ли студентыспециальности история и иностранный язык студентов специальности история и
психология по уровню вербального интеллекта.
Манна-Уитни, определите, превосходят ли студентыспециальности история и иностранный язык студентов специальности история и
психология по уровню вербального интеллекта.
382. Используя критерий Вилкоксона, определите значимость различий изменений
вербальной памяти после иппотерапии по результатам следующего эксперимента:
| 1-е измерение (до) |
6 |
5 |
4 |
3 |
7 |
6 |
4 |
4 |
5 |
6 |
| 2-е измерение (после) |
8 |
5 |
6 |
4 |
7 |
7 |
5 |
4 |
8 |
7 |
383. При изучении психологического влияния иппотерапии на связь
эмоционального состояния и зрительной памяти получены следующие результаты:
| Кол-во выборов, соотв. положительному эмоциональному
состоянию (баллы) |
3 |
3 |
2 |
1 |
3 |
2 |
1 |
1 |
3 |
2 |
3 |
2 |
3 |
2 |
3 |
3 |
2 |
3 |
2 |
1 |
| Зрительная память
(баллы) |
6 |
5 |
5 |
3 |
5 |
5 |
4 |
3 |
6 |
3 |
5 |
5 |
6 |
6 |
5 |
6 |
5 |
4 |
5 |
4 |
Существенна ли связь эмоционального состояния и зрительной памяти под
влиянием иппотерапии?
384. Соотношение средних величин невербального, вербального и общего IQ в
различных системах обучения дало следующие результаты:
| Система обучения |
IQ |
IQ |
IQ |
| Традиционная |
113 |
116 |
116 |
| Л.В. Занкова |
111 |
121 |
118 |
| Д.Б. Эльконина -
В.В. Давыдова |
120 |
131 |
128 |
Применяя критерий 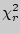 Фридмана, покажите, являются ли полученные
результаты случайными.
Фридмана, покажите, являются ли полученные
результаты случайными.
385. В выборке курсантов военного училища измерялась способность к удержанию
физического волевого усилия на динамометре. Сначала у испытуемых измерялась
максимальная мышечная сила каждой из рук, а на следующий день им
предлагалось выдерживать на динамометре с подвижной стрелкой мышечное
усилие, равное
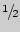 максимальной мышечной силы
данной руки. Почувствовав усталость, испытуемый сообщает об этом
экспериментатору, но не прекращает опыт, преодолевая усталость ("бороться,
пока воля не иссякнет"). Опыт проводился дважды; вначале с обычной
инструкцией, а затем после того, как испытуемый заполнял опросник самооценки
волевых качеств по методике Пуни и дал следующие результаты:
максимальной мышечной силы
данной руки. Почувствовав усталость, испытуемый сообщает об этом
экспериментатору, но не прекращает опыт, преодолевая усталость ("бороться,
пока воля не иссякнет"). Опыт проводился дважды; вначале с обычной
инструкцией, а затем после того, как испытуемый заполнял опросник самооценки
волевых качеств по методике Пуни и дал следующие результаты:
| |
Длительность удержания усилия на
динамометре |
|
|
|
| № испытуемого |
До изучения волевых качеств и обращения к
идеалу (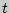 до) до) |
После измерения волевых качеств и обращения к
идеалу (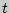 после) после) |
Разность
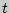 после - после - 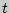 до до |
Абсо
лютное
значение
разности |
Ранговый номер абсолютной разности |
| 1
2
3
4
5
6
7
8
9
10
11 |
64
77
74
95
105
83
73
75
101
97
78 |
25
50
77
76
67
75
77
71
63
122
60 |
|
|
|
Применяя критерий Вилкоксона, подтвердите или опровергните гипотезу
экспериментатора о том, что обращение к идеалу способствует возрастанию
волевого усилия.
386. Используя критерий Пирсона, определите, различаются ли распределения
мужских и женских имен у двух писателей, А. и Б. Эмпирические частоты
приведены в таблице:
| |
Мужчин |
Женщин |
Всего человек |
| Писатель А.
Писатель Б. |
22
68 |
45
115 |
67
183 |
| Суммы |
90 |
160 |
250 |
II 387. Изучалась проблема психологических барьеров при обращении в
службу знакомств у мужчин и женщин. В эксперименте участвовали 17 мужчин и
23 женщины в возрасте от 17 до 45 лет (средний возраст 32,5 года).
Испытуемые должны были отметить на отрезке точку, соответствующую
интенсивности внутреннего сопротивления, которое им пришлось преодолеть,
чтобы обратиться в службу знакомств. Длина отрезка, отражающая максимально
возможное сопротивление, составляла 100 мм. В таблице приведены показатели
интенсивности сопротивления, выраженные в миллиметрах.
Группа 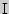 - мужчины - мужчины
(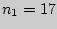 ) ) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
| Длина отрезка "сопротивления" |
81 |
80 |
73 |
72 |
72 |
69 |
69 |
65 |
65 |
62 |
60 |
54 |
54 |
43 |
30 |
26 |
26 |
Группа
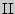 - женщины - женщины
(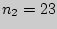 ) ) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
| Длина отрезка |
70 |
66 |
66 |
63 |
63 |
61 |
60 |
54 |
47 |
43 |
41 |
40 |
39 |
38 |
38 |
35 |
30 |
27 |
25 |
23 |
17 |
10 |
9 |
Можно ли утверждать, что мужчинам приходится преодолевать субъективно более
мощное сопротивление?
388. 12 участников комплексной программы тренинга партнерского общения,
продолжавшегося 7 дней, дважды оценивали у себя уровень владения тремя
важнейшими коммуникативными навыками. Участники должны были наметить для
себя и реально достижимый, с их точки зрения, индивидуальный идеал в
развитии каждого из навыков. Измерения проводились по 10-балльной шкале и
дали следующие результаты:
| |
1-е измерение |
2-е измерение |
| № участника |
Активное слушание |
Снижение эмоционального напряжения |
Аргумен
тация |
Активное слушание |
Снижение эмоционального напряжения |
Аргумен
тация |
| |
Реал. |
Идеал. |
Реал. |
Идеал. |
Реал. |
Идеал. |
Реал. |
Идеал. |
Реал. |
Идеал. |
Реал. |
Идеал. |
| 1
2
3
4
5
6
7
8
9
10 |
6
3
4
4
6
6
3
6
6
5 |
9
5
6
6
9
8
8
9
8
8 |
5
1
4
4
4
5
5
5
5
6 |
8
3
6
5
9
8
10
8
9
9 |
5
4
5
5
4
3
2
3
5
5 |
8
5
8
7
8
6
6
7
9
8 |
7
5
8
6
4
8
7
5
7
7 |
10
7
10
7
10
9
8
8
8
10 |
6
4
7
5
5
7
8
7
6
7 |
10
6
8
7
10
9
10
10
9
10 |
7
5
6
5
5
6
5
5
5
6 |
9
7
8
7
10
8
7
9
9
10 |
Ощущаются ли участниками достоверные сдвиги в уровне владения каждым из трех
навыков после тренинга? Уменьшается ли расхождение между "идеальным" и
реальным уровнем владения навыками после тренинга?
III 389. Экспериментально проверяется одно из положений модели
Теретлуна, а именно, гипотеза о том, что ошибка при опознании стимула имеет
дисперсию, не зависящую от интенсивности или другой физической меры стимула.
Стимул интенсивности 10 усл. ед. оценивается как 9, 9, 8, 10, 12, 13, 10,
10, 12, а стимул интенсивности 20 усл. ед. оценивается как 15, 16, 17, 23,
22, 20, 21, 24, 27. В пользу проверяемой гипотезы или против нее
свидетельствуют приведенные факты?
390. В опытах по изучению объема памяти испытуемых предлагали заучивать
последовательности из восьми трехзначных чисел. В одной серии числа отбирали
из 64 известных испытуемому чисел, а в другой серии - из 512. В опытах
участвовали 15 испытуемых. С каждым из них в каждой серии было проведено по
10 опытов. Результаты эксперимента представлены в таблице:
| № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| Среднее знач-е числа повторений в 1-м опыте |
3,6 |
4,8 |
7,0 |
4,3 |
6,4 |
4,3 |
5,0 |
5,2 |
4,1 |
6,1 |
4,2 |
3,8 |
3,2 |
3,8 |
3,9 |
| Среднее знач-е числа повторений во 2-м опыте |
2,6 |
4,3 |
3,9 |
4,0 |
3,0 |
3,9 |
4,7 |
3,9 |
4,6 |
4,4 |
3,5 |
3,4 |
3,1 |
3,1 |
3,1 |
Значимы ли различия между рядами полученных чисел или имеющиеся расхождения
можно считать случайными? Сформулируйте проверяемые гипотезы и обоснуйте
выбор статистического критерия.
Далее: §40. Статистические методы в
Вверх: Глава V. Математическая статистика
Назад: §38. Критерии Пирсона и
ЯГПУ, Центр информационных технологий обучения
2006-03-04
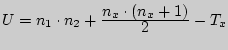 ,
где
,
где 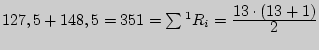
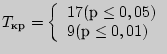

![\begin{displaymath}
\mbox{\boldmath$(r)$} = \left[ {{\begin{array}{*{20}c}
1 \h...
...ill \\
\hfill & \hfill & 1 \hfill \\
\end{array} }} \right]
\end{displaymath}](img1992.png)