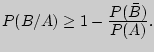Условной вероятностью ![]() события
события ![]() при
условии, что событие
при
условии, что событие ![]() произошло
произошло ![]() назовем отношение
назовем отношение
![]() .
.
Это определение эквивалентно так называемой теореме умножения,
согласно которой
![]() , т.е.
вероятность
произведения двух
событий равна вероятности одного из них, умноженной на условную
вероятность
другого при условии, что первое событие наступило.
, т.е.
вероятность
произведения двух
событий равна вероятности одного из них, умноженной на условную
вероятность
другого при условии, что первое событие наступило.
Два события ![]() и
и ![]() называются
независимыми, если
называются
независимыми, если ![]() .
.
Построение классической вероятности основано на правилах сложения и умножения вероятностей, следствия которых имеют следующие интерпретации на вероятностных деревьях:
1.
![]() ,
где
,
где ![]() и
и ![]() -
несовместные
события
-
несовместные
события
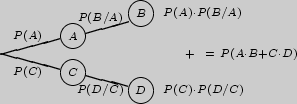
2.
![]()

Назовем произведение
![]() весом ветви, проходящей через корень дерева и вершины, соответствующие
событиям
весом ветви, проходящей через корень дерева и вершины, соответствующие
событиям ![]()
![]() .
.
Интерпретацией теорем сложения и умножения на вероятностных деревьях служит дерево исходов, соответствующее "благоприятному" событию. Рядом с каждым ребром такого дерева запишем вероятность исхода, соответствующего конечной вершине этого ребра при условии выполнения произведения всех исходов, соответствующих вершинам пути от корня дерева до данной вершины.
Эффективность данных интерпретаций покажем на следующих примерах.
Пример 26. Слово "МАТЕМАТИКА" разделено на отдельные буквы, из них произвольным образом отбираются и выкладываются по порядку четыре буквы. Какова вероятность получения слова "МАМА"?
Решение. Пусть событие ![]() = {получить слово "МАМА"}.
Возьмем в дереве
испытаний ветвь, соответствующую событию
= {получить слово "МАМА"}.
Возьмем в дереве
испытаний ветвь, соответствующую событию ![]() и
найдем ее вес:
и
найдем ее вес:
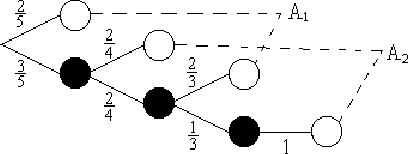
Пример 27. Два игрока по очереди выбирают вслепую фишку из имеющихся 2 белых и 3 черных. Побеждает тот, кто первым вытянет белую фишку. В каком отношении находятся шансы игроков на успех?
Решение. Обозначим через ![]() = {победа
= {победа ![]() -го
игрока},
-го
игрока}, ![]() 1, 2. Составим
вероятностное дерево исходов данного испытания.
1, 2. Составим
вероятностное дерево исходов данного испытания.
Пример 28. Четыре брата определяют дежурного по квартире при помощи четырех спичек, одна из которых короче остальных. В равных ли условиях находятся братья?
Решение. Пусть четверо вытягивают по очереди одну спичку до тех пор, пока кто-нибудь не вытянет короткую. Тот, кто вытянет короткую спичку, станет дежурным.
Вероятностное дерево исходов будет иметь вид:
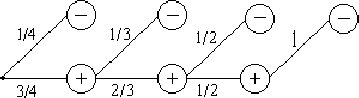
и, следовательно, в этом случае шансы у всех равные.
Пример 29. Доказать, что
![]() где n
где n![]() a и n
a и n![]() b.
b.
Решение. Возьмем урну, содержащую ![]() белых и
белых и ![]() черных шаров. Пусть
черных шаров. Пусть
![]() = {вынимание
= {вынимание ![]() шаров} и
шаров} и ![]() = {вынимание
= {вынимание ![]() белых
шаров}. Тогда
белых
шаров}. Тогда
![]() +...+
+...+ ![]() и 1
=
и 1
= ![]() =
=
![]() +...+
+...+
![]() =
=
Пример 30 (пример Бернштейна). Доказать, что вообще говоря
![]() для
попарно независимых событий
для
попарно независимых событий ![]() ,
, ![]() (i
(i![]() j) /сравни с
вероятностью суммы попарно несовместных событий/.
j) /сравни с
вероятностью суммы попарно несовместных событий/.
Решение. Рассмотрим 9 карточек, на которых написаны упорядоченные
тройки
букв ![]() :
:
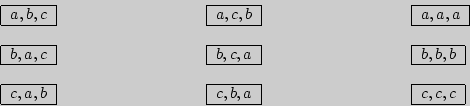
Примем за событие ![]() = {достать карточку с буквой
= {достать карточку с буквой ![]() на
на ![]() -м месте}.
-м месте}.
События ![]() и
и ![]() независимы, поскольку
независимы, поскольку
![]()
Аналогично доказывается, что ![]() ,
, ![]() и
и ![]() ,
, ![]() тоже попарно
независимые события.
тоже попарно
независимые события.
Однако
![]()
Вопросы для самоконтроля
Задачи
а)
![]()
б)
![]()
в)
![]()
г)
![]()