| 0 |
30 |
45 |
60 |
90 |
|
|---|---|---|---|---|---|
| 0 |
|
|
|
|
|
| sin |
0 |
|
|
|
1 |
| сos |
1 |
|
|
|
0 |
| tg |
0 |
|
1 | - | |
| ctg |
- | 1 |
|
0 |
Первоначально синус, косинус, тангенс и котангенс рассматриваются как тригонометрические функции острого угла. Далее в разделе ``Тригонометрия'' проводится обобщение этих понятий, и указанные функции рассматриваются как функции действительного числа.
Здесь учитывается, что для любого действительного числа х существует угол, радианная мера которого равна х. Одним из ведущих свойств тригонометрических функций является периодичность.
Определение: Функцию
![]() называют
периодической, если существует число
называют
периодической, если существует число ![]() такое, что для любого
такое, что для любого ![]() из области
определения функции
из области
определения функции
![]() чи?сла
чи?сла ![]() и
и ![]() также
входят в область определения функции
также
входят в область определения функции
![]() и выполняется
равенство:
и выполняется
равенство:
![]() .
.
Число ![]() называют периодом функции
называют периодом функции
![]() . Наименьший положительный
период функции называют ее главным периодом.
. Наименьший положительный
период функции называют ее главным периодом.
1. Функция y = sin x.
Область определения - все множество действительных чисел R.
Область изменения - отрезок [- 1; 1].
Функция
![]() нечетная; периодическая с главным периодом
нечетная; периодическая с главным периодом
![]() ; непрерывная на всей области определения. На промежутках
; непрерывная на всей области определения. На промежутках
![]() функция
функция ![]() = sin
= sin ![]() возрастает, а на промежутках
возрастает, а на промежутках
![]() убывает.
убывает.
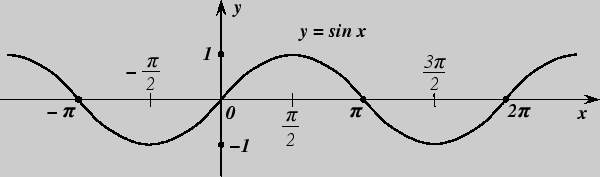
График функции ![]() = sin
= sin ![]() называется синусоидой.
называется синусоидой.
2. Функция y = соs x.
Область определения - все множество действительных чисел R.
Область изменения - отрезок [- 1; 1].
Функция
![]() четная; периодическая с главным периодом
четная; периодическая с главным периодом
![]() ; непрерывная на всей области определения. На промежутках
; непрерывная на всей области определения. На промежутках
![]() функция
функция
![]() убывает, а на промежутках
убывает, а на промежутках
![]() возрастает.
возрастает.
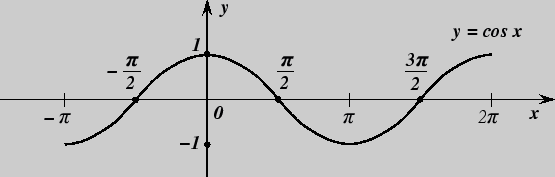
График функции ![]() = sin
= sin ![]() называется косинусоидой.
называется косинусоидой.
3. Функция y = tg x.
Область определения - множество действительных чисел, отличных от чисел
![]() , где
, где
![]() .
.
Область изменения -
![]() .
.
Функция ![]() = tg
= tg ![]() нечетная; периодическая с главным периодом
нечетная; периодическая с главным периодом ![]() . Функция
непрерывна и возрастает на промежутках
. Функция
непрерывна и возрастает на промежутках
![]() .
.
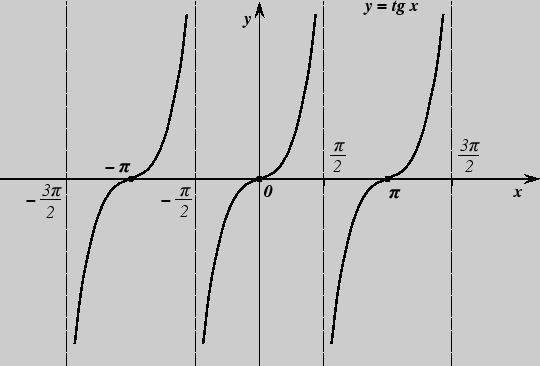
График функции ![]() = tg
= tg ![]() называется тангенсоидой.
называется тангенсоидой.
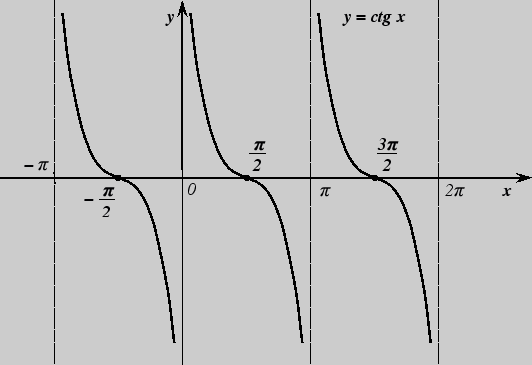
4. Функция y = сtg x.
Область определения - множество действительных чисел, отличных от чисел
![]() , где
, где
![]() .
.
Область изменения -
![]() .
.
Функция ![]() = сtg
= сtg ![]() нечетная; периодическая с главным периодом
нечетная; периодическая с главным периодом ![]() . Функция
непрерывна и убывает на промежутках
. Функция
непрерывна и убывает на промежутках
![]() .
.
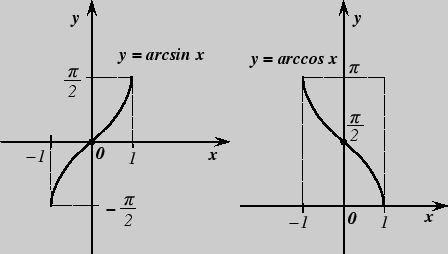
| 1. Функция y = arcsin x | 2. Функция y = arcсоs x |
|---|---|
| Область определения: [- 1; 1]
Область изменения:
Возрастает на [- 1; 1] Непериодическая, нечетная |
Область определения: [- 1; 1]
Область изменения:
Убывает на [- 1; 1] Непериодическая |
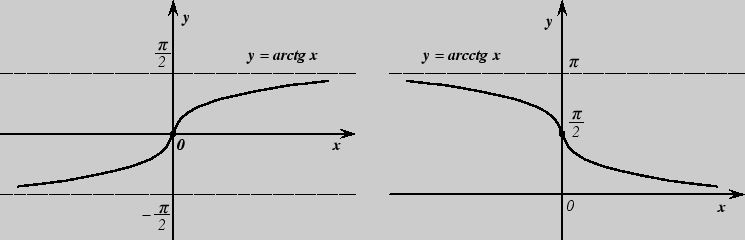
| 3. Функция y = arctg x | 4. Функция y = arсctg x |
|---|---|
| Область определения:
Область изменения:
Возрастает на
Непериодическая, нечетная |
Область определения:
Область изменения:
Убывает на
Непериодическая |
Для решения тригонометрических уравнений и неравенств применяется единичная
окружность, совмещенная с системой координат. Величина sin x отмечается по оси
ординат; величина cos х по оси абсцисс; величина tg x отмечается на прямой тангенсов
![]() 1 от точки (1;0); величина ctg x отмечается на прямой котангенсов
1 от точки (1;0); величина ctg x отмечается на прямой котангенсов ![]() = 1 от точки
(0; 1).
= 1 от точки
(0; 1).
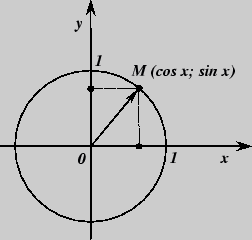
1. sin
![]() + cos
+ cos
![]() = 1; 2. 1 + tg
= 1; 2. 1 + tg
![]() =
=
![]() ; 3. 1 + ctg
; 3. 1 + ctg
![]() ;
4. tg
;
4. tg ![]() ctg
ctg ![]() = 1.
= 1.
| 1. sin (
2. sin (
3. sin 2 |
4. cos (
5. cos (
6. cos 2 |
|---|
1. sin ![]() + sin
+ sin ![]() = 2
= 2
![]() ;
3. cos
;
3. cos ![]() + cos
+ cos ![]() = 2
= 2
![]() ;
;
2. sin ![]() - sin
- sin ![]() = 2
= 2
![]() ;
4. cos
;
4. cos ![]() - cos
- cos ![]() = -2
= -2
![]() .
.
Примеры: 1. Упростить: а) (sin ![]() - cos
- cos ![]() - sin
2
- sin
2![]() Данное выражение преобразуется к виду sin
Данное выражение преобразуется к виду sin![]() + 2sin
+ 2sin ![]() cos
cos ![]() + cos
+ cos![]() - sin 2
- sin 2![]() = sin
= sin
![]() + cos
+ cos
![]() +2sin
+2sin ![]() cos
cos ![]() - sin 2
- sin 2![]() =
=
= 1 + sin 2![]() - sin 2
- sin 2![]() = 1;
= 1;
б)
![]() =
2 сos 20
=
2 сos 20![]() .
.
2. Вычислить: а) sin 74![]() cos 16
cos 16![]() + cos 74
+ cos 74![]() sin 16
sin 16![]() = sin
(74
= sin
(74![]() + 16
+ 16![]() = sin 90
= sin 90![]() = 1;
= 1;
б)
![]() = tg 120
= tg 120![]() = tg (90
= tg (90![]() +
30
+
30![]() = - ctg 30
= - ctg 30
![]() .
.
|
|
|
|
|
|
|
|
||
| sin |
sin |
-sin |
sin |
-sin |
cos |
cos |
-cos |
-cos |
| cos |
cos |
cos |
-cos |
-cos |
sin |
-sin |
-sin |
sin |
| tg |
tg |
-tg |
-tg |
tg |
ctg |
-ctg |
ctg |
-ctg |
| ctg |
ctg |
-ctg |
-ctg |
ctg |
tg |
-tg |
tg |
-tg |
| 1. arcsin (-
2. arccos (-
3. arcsin |
4. arctg (-
5. arcctg (-
6. arctg |
Примеры: Вычислить: а) arcsin (-
![]() = -
arcsin
= -
arcsin
![]() ;
;
б) arccos (-
![]() arccos
arccos
![]() -
-
![]() ; в) arctg (-
; в) arctg (-
![]() arctg
arctg
![]() .
.