По соотношению сторон треугольники разделяются на разносторонние и равнобедренные (в том числе и равносторонние).
По величине наибольшего угла треугольники разделяются на остроугольные, прямоугольные и тупоугольные.
Признаки равенства треугольников:
1. По двум сторонам и углу между ними:
2. По стороне и двум прилежащим к ней углам:
3. По трем сторонам:
Признаки подобия треугольников:
1.
![]() , если
, если
![]() .
.
2.
![]() , если
, если
![]() .
.
3.
![]() , если
, если
![]() .
.
Средняя линия - отрезок, соединяющий середины двух сторон треугольника.
Медиана - отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса - отрезок, выходящий из вершины треугольника и делящий угол пополам.
Биссектриса угла треугольника делит его противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Высота - отрезок, выходящий из вершины треугольника и перпендикулярный противоположной стороне.
Срединный перпендикуляр - прямая, проведенная через середину стороны треугольника, перпендикулярная к этой стороне.
Четыре замечательные точки треугольника:
1. Точка пересечения медиан (медианы ![]() пересекаются в одной точке).
пересекаются в одной точке).
2. Точка пересечения биссектрис - центр вписанной окружности (биссектрисы
![]() пересекаются в одной точке).
пересекаются в одной точке).
3. Точка пересечения высот (высоты ![]() пересекаются в одной точке).
пересекаются в одной точке).
4. Точка пересечения срединных перпендикуляров - центр описанной окружности
(срединные перпендикуляры ![]() пересекаются в одной точке).
пересекаются в одной точке).
Две прямые на плоскости называются параллельными, если они не пересекаются.
Аксиома параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы
равны, соответственные углы равны, а сумма односторонних углов равна ![]() .
.
Четырехугольники могут быть выпуклыми и невыпуклыми.
Выпуклые четырехугольники по наличию параллельных сторон делятся на параллелограммы (2 пары параллельных сторон), трапеции (1 пара параллельных сторон) и общего вида (нет параллельных сторон).
К частным видам параллелограммов относятся прямоугольники (4 угла прямые), ромбы (4 стороны равны), квадраты (обладают свойствами как прямоугольников, так и ромбов).
Свойства параллелограммов:
- В любом параллелограмме противоположные стороны равны, противоположные углы равны, диагонали в точке пересечения делятся пополам.
- В прямоугольнике диагонали равны.
- В ромбе диагонали перпендикулярны.
Признаки параллелограмма:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
К частным видам трапеций относятся равнобедренные (боковые стороны равны) и прямоугольные (одна из боковых сторон перпендикулярна основаниям).
Свойства трапеций:
- Средняя линия трапеции (отрезок, соединяющий середины боковых сторон) параллельна основаниям трапеции, а длина ее равна полусумме длин оснований.
- В равнобедренной трапеции диагонали равны, углы при одном и том же основании равны.
Окружность - геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Окружность является замкнутой плоской линией.
Круг - часть плоскости, ограниченная окружностью.
Радиус - отрезок, соединяющий центр окружности с точкой на окружности.
Хорда - отрезок, соединяющий две произвольные точки окружности.
Диаметр - хорда, проходящая через центр окружности.
Центральный угол - угол между двумя радиусами, его величина совпадает с градусной мерой дуги, на которую он опирается.
Вписанный угол - угол между двумя хордами, с вершиной на окружности; измеряется половиной градусной меры дуги, на которую он опирается.
Если проведены две хорды AB и CD окружности, пересекающиеся в точке Р, то
выполняется равенство
![]() .
.
Если две хорды окружности параллельны, то градусные меры дуг, заключенных между ними, равны.
Касательная к окружности - прямая, имеющая с окружностью одну общую точку. Радиус, проведенный в точку касания, перпендикулярен касательной.
Угол между касательной и хордой, проведенными через точку окружности, измеряется половиной градусной меры дуги, заключенной между касательной и хордой.
Теорема Птолемея для вписанных четырехугольников: Произведение длин диагоналей вписанного четырехугольника ABCD равно сумме произведений длин пар противоположных сторон:
Если четырехугольник вписан в окружность, то суммы его противолежащих углов
равны ![]() .
.
Если четырехугольник ABCD описан около окружности, то суммы длин его противоположных сторон равны.
1. Произвольный треугольник (![]() - стороны;
- стороны; ![]() ,
,
![]() ,
, ![]() -
- ![]() ротиволежащие им углы;
ротиволежащие им углы; ![]() - полупериметр;
- полупериметр; ![]() -
радиус описанной окружности;
-
радиус описанной окружности; ![]() - радиус вписанной окружности;
- радиус вписанной окружности; ![]() - площадь;
- площадь;
![]() - высота, проведенная к стороне
- высота, проведенная к стороне ![]() :
:
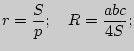
![]() (теорема косинусов);
(теорема косинусов);
![]() (теорема синусов).
(теорема синусов).
2. Прямоугольный треугольник (![]() - катеты;
- катеты;![]() - гипотенуза;
- гипотенуза;
![]() - проекции катетов на гипотенузу;
- проекции катетов на гипотенузу; ![]() - высота, проведенная к
гипотенузе):
- высота, проведенная к
гипотенузе):
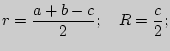
![]() (теорема Пифагора);
(теорема Пифагора);
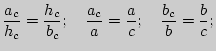
3. Равносторонний треугольник:
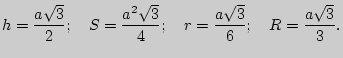
4. Произвольный выпуклый четырехугольник (![]() и
и
![]() - диагонали;
- диагонали; ![]() - угол между ними;
- угол между ними; ![]() - площадь):
- площадь):
5. Параллелограмм (![]() и
и![]() - смежные стороны;
- смежные стороны; ![]() - угол
между ними;
- угол
между ними; ![]() - высота, проведенная к стороне
- высота, проведенная к стороне ![]() ;
;![]() - площадь):
- площадь):
6. Ромб:
![]() .
.
7. Прямоугольник:
![]() .
.
8. Квадрат (![]() - диагональ):
- диагональ):
![]() .
.
9. Трапеция (![]() и
и ![]() - основания;
- основания; ![]() - расстояние между ними;
- расстояние между ними;
![]() - средняя линия;
- средняя линия; ![]() - площадь):
- площадь):
10. Описанный многоугольник (![]() - полупериметр;
- полупериметр; ![]() - радиус
вписанной окружности;
- радиус
вписанной окружности; ![]() - площадь):
- площадь): ![]() .
.
11. Правильный многоугольник (![]() - сторона
правильного
- сторона
правильного ![]() -угольника;
-угольника; ![]() - радиус описанной окружности;
- радиус описанной окружности; ![]() - радиус
вписанной окружности;
- радиус
вписанной окружности; ![]() - площадь):
- площадь):
12. Окружность, круг (![]() - радиус;
- радиус; ![]() - длина окружности;
- длина окружности;
![]() - площадь круга):
- площадь круга):
13. Сектор (![]() - длина дуги, ограничивающей сектор;
- длина дуги, ограничивающей сектор; ![]() -
градусная мера центрального угла;
-
градусная мера центрального угла; ![]() - радианная мера центрального
угла;
- радианная мера центрального
угла; ![]() - радиус;
- радиус; ![]() - площадь):
- площадь):
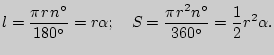
Задача 1. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найти катеты треугольника.
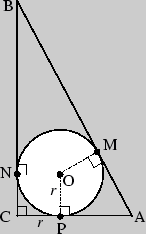
АМ = 5; ВМ = 12. Пусть радиус вписанной окружности равен ![]() см.
см.
По свойствам отрезков касательных, проведенных к окружности из внешней точки: BM = BN, AM = AP.
Тогда BC = BN + NC = 12 + ![]() ,
,
AC = AP + PC = 5 + ![]() , AB = BM + MA = 12 + 5 = 17.
, AB = BM + MA = 12 + 5 = 17.
По теореме Пифагора АВ![]() = АС
= АС![]() + ВС
+ ВС![]() .
.
(![]() + 12)
+ 12)![]() + (
+ (![]() + 5)
+ 5)![]() = 17
= 17![]() .
.
Упростив уравнение, получим ![]() + 17
+ 17![]() - 6 = .
- 6 = .
Его корни ![]() = - 2 (посторонний) и
= - 2 (посторонний) и ![]() = 3.
= 3.
Тогда АС = 5 + 3 = 8; ВС = 12 + 3 = 15.
Ответ: 8 см, 15 см.
Задача 2. В параллелограмме ABCD со стороной AD = 25 проведена
биссектриса угла А, проходящая через точку Р на стороне ВС. Найдите периметр
трапеции APCD, если ее средняя линия равна 15, а диагональ
![]() .
.
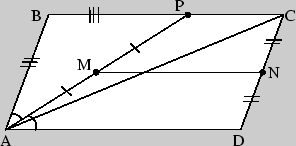
1)
![]() , так как АР - биссектриса; тогда
, так как АР - биссектриса; тогда ![]() АВР - равнобедренный (АВ = ВР);
АВР - равнобедренный (АВ = ВР);
2) MN - средняя линия трапеции APCD: 2MN = AD + PC; AD + PC = 30; PC = 5; BP = 20; AB = 20.
По теореме косинусов:
3) В ![]() АВР: AP
АВР: AP![]() = AB
= AB![]() +BP
+BP![]() - 2AB
- 2AB![]() BP
BP![]() cos
cos![]() AВР.
AВР.
4) В ![]() АВC: AC
АВC: AC![]() = AB
= AB![]() + BC
+ BC![]() - 2AB
- 2AB![]() BC
BC![]() cos
cos![]() AВР.
AВР.
Из 4) находим cos![]() AВР =
AВР =
![]() ; подставив найденное
значение в 3), получим АР
; подставив найденное
значение в 3), получим АР![]() = 900, АР = 30.
= 900, АР = 30.
5) ![]() = AP + РС + CD + DА = 30 + 5 + 20 + 25 = 80.
= AP + РС + CD + DА = 30 + 5 + 20 + 25 = 80.
Ответ: 80.
Задача 3. Сторона правильного шестиугольника ABCDEF равна ![]() . Найдите радиус окружности, вписанной в треугольник МРК, где точки М, Р,
К - середины сторон шестиугольника ABCDEF соответственно.
. Найдите радиус окружности, вписанной в треугольник МРК, где точки М, Р,
К - середины сторон шестиугольника ABCDEF соответственно.
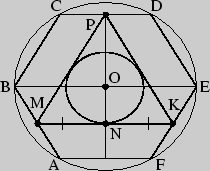
1) По свойствам правильного шестиугольника BE = 2 AF = ![]() .
.
2) ABEF - равнобедренная трапеция, в которой МК - средняя линия: МК =
![]() .
.
3)
![]() РК - равносторонний. Радиус искомой вписанной
окружности
РК - равносторонний. Радиус искомой вписанной
окружности
![]() PN, PN =
PN, PN =
![]() МК.
МК.
PN =
![]() = 72, следовательно,
= 72, следовательно, ![]() = 24.
= 24.
Ответ: 24.
Задача 4. Углы при одном из оснований трапеции равны ![]() и
и
![]() , а разность квадратов длин ее оснований равна 8. Найти площадь
трапеции.
, а разность квадратов длин ее оснований равна 8. Найти площадь
трапеции.
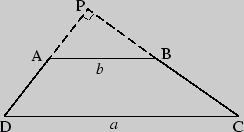
В трапеции
![]() ,
,
![]() .
.
Продолжим боковые стороны AD и ВС до пресечения их в точке Р. ![]() CРD
- прямоугольный, так как
CРD
- прямоугольный, так как
![]() .
.
S![]() = S
= S
![]() - S
- S
![]()
Пусть AB = ![]() , CD =
, CD = ![]() ; по условию
; по условию ![]() -
- ![]() = 8, AB
= 8, AB
![]() CD.
CD.
S
![]() CP
CP ![]() DP; S
DP; S
![]() =
=
![]() PB
PB ![]() PA.
PA.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
![]() .
.
S
![]() -
-
![]() =
=
![]() -
-
![]() 8 = 1.
8 = 1.
Ответ: 1.