1)
![]() ; 2)
; 2)
![]() ;
3)
;
3)
![]() ; 4)
; 4)
![]() ; 5)
; 5)
![]() .
.
Примеры:
а)
![]() ; б)
; б)
![]() .
.
1)
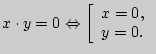 ; 2)
; 2)
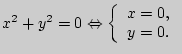 ; 3)
; 3)
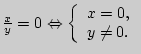 ;
;
4)
![]() ;
;
5) теорема Виета: если
![]() где
где
![]() корни уравнения, то:
корни уравнения, то:
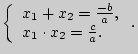
Примеры:
а)
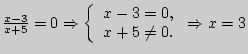 ;
;
б)
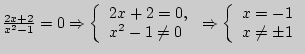 , следовательно, нет решения;
, следовательно, нет решения;
в)
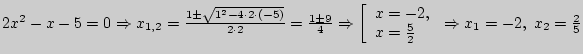 ;
;
г)
![]() , по теореме Виета:
, по теореме Виета:
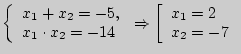 ;
;
д)
![]() .
.
1)
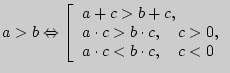 2)
2)
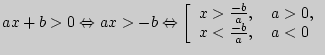 .
.
Примеры: а)
![]() ; б)
; б)
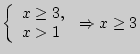 ; в)
; в)
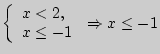 ;
;
г)
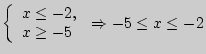 ; д)
; д)
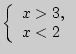 нет решения.
нет решения.
План решения неравенства
![]() ) методом интервалов:
) методом интервалов:
1. Раскладываем числитель и знаменатель левой части на множители.
2. Наносим на числовую ось корни знаменателя в виде выколотых точек и корни числителя: если неравенство строгое - в виде выколотых точек, если нестрогое - в виде невыколотых точек.
3. Отмечаем интервалы, на которых дробь
![]() сохраняет знак, и расставляем знаки этой дроби на каждом
интервале.
сохраняет знак, и расставляем знаки этой дроби на каждом
интервале.
4. Выбираем для ответа интервалы с нужным знаком (в соответствии со знаком неравенства).