Далее: II. Элементы математического анализа
Вверх: I. Элементы аналитической геометрии
Назад: 3. Системы линейных уравнений
Вопросы теории. Матрицы, действия над матрицами и их основные
свойства. Транспонирование матрицы. Согласование размеров матриц при их перемножении. Некоммутативность
умножения матриц. Определители и их основные свойства. Правило Лапласа. Решение
систем линейных уравнений по правилу Крамера. Обратная матрица. Критерий
обратимости матрицы.
Образцы решения задач
Задача 1. Выполните операции над матрицами:  , где
, где
 - единичная матрица.
- единичная матрица.
Решение. Сложение матриц и умножение матрицы на число выполняются
покомпонентно, поэтому
Задача 2. Для данных матриц 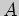 и
и 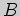 выясните, определены
ли произведения
выясните, определены
ли произведения  ,
,  ,
,  и
и  и вычислите те из них, которые
определены:
Решение. Матрица
и вычислите те из них, которые
определены:
Решение. Матрица 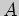 имеет размеры
имеет размеры  , а матрица
, а матрица
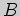 - размеры
- размеры  . Поэтому произведение
. Поэтому произведение  не определено, так как
число столбцов матрицы
не определено, так как
число столбцов матрицы 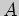 не равно числу строк матрицы
не равно числу строк матрицы 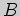 . Число
столбцов матрицы
. Число
столбцов матрицы 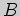 равно числу строк матрицы
равно числу строк матрицы 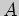 , поэтому произведение
, поэтому произведение
 определено и равно
Число столбцов матрицы
определено и равно
Число столбцов матрицы 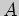 не равно числу ее строк, поэтому ее квадрат
не равно числу ее строк, поэтому ее квадрат
 не определен. Матрица
не определен. Матрица 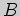 квадратная, поэтому ее квадрат определен
и равен
квадратная, поэтому ее квадрат определен
и равен
Задача 3. Вычислите определитель
Решение. Все элементы четвертой строки определителя имеют общий
множитель  , который можно вынести за знак определителя:
Получившийся определитель нетрудно вычислить, пользуясь правилом Лапласа и
разлагая по первому столбцу. Единственный ненулевой элемент этого столбца
находится в третьей строке, поэтому соответствующий ему минор войдет в
выражение для определителя со знаком "+":
, который можно вынести за знак определителя:
Получившийся определитель нетрудно вычислить, пользуясь правилом Лапласа и
разлагая по первому столбцу. Единственный ненулевой элемент этого столбца
находится в третьей строке, поэтому соответствующий ему минор войдет в
выражение для определителя со знаком "+":
 :
:
Задача 4. Решите систему, пользуясь правилом Крамера:
Решение. Согласно правилу Крамера, для решения системы необходимо
вычислить определители
Искомые 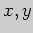 равны
Задача 5. Вычислите матрицу, обратную данной:
равны
Задача 5. Вычислите матрицу, обратную данной:
![$ A=\left[ \begin{array}{rr}
3&1\\
2&1
\end{array} \right].
$](img239.png)
Решение. Вычисляя определитель данной матрицы
видим, что матрица имеет обратную. Вычисляем алгебраические дополнения  элементов матрицы (здесь
элементов матрицы (здесь  - минор, получаемый вычеркиванием строки и
столбца, содержащих данный элемент):
Осталось подставить значения алгебраических дополнений в формулу для вычисления
обратной матрицы (обратите внимание на порядок следования алгебраических
дополнений!):
- минор, получаемый вычеркиванием строки и
столбца, содержащих данный элемент):
Осталось подставить значения алгебраических дополнений в формулу для вычисления
обратной матрицы (обратите внимание на порядок следования алгебраических
дополнений!):
Задачи для самостоятельного решения
1. Выполните действия: 


 Символ
Символ  означает транспонирование матрицы.
означает транспонирование матрицы.
2. Для данных матриц 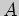 и
и 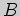 выясните, определены ли произведения
выясните, определены ли произведения
 ,
,  ,
,  и
и  . Вычислите те произведения, которые определены.
. Вычислите те произведения, которые определены.
3. Вычислите и сравните произведения  и
и  . Найдите
. Найдите
 .
4. Вычислите
.
4. Вычислите  ,
,  ,
,  и сравните результаты.
и сравните результаты.
5. Вычислите определители:
6. Решите системы, пользуясь правилом Крамера.
7. Среди данных матриц найдите обратимые и вычислите для них
обратные
матрицы. Результат проверьте умножением.
Далее: II. Элементы математического анализа
Вверх: I. Элементы аналитической геометрии
Назад: 3. Системы линейных уравнений
ЯГПУ, Центр информационных технологий обучения
27.03.2007
![]() , где
, где
![$\displaystyle A=\left[ \begin{array}{rrr}
0&-1&1\\
-5&0&2\\
0&0&1
\end{array}...
...;\; B=\left[ \begin{array}{rrr}
3&-1&0\\
0&2&-3\\
1&1&0
\end{array} \right],
$](img213.png)
![$\displaystyle 2A-3B+I=2\left[ \begin{array}{rrr}
0&-1&1\\
-5&0&2\\
0&0&1
\end...
...\right]+\left[ \begin{array}{rrr}
1&0&0\\
0&1&0\\
0&0&1
\end{array} \right]=
$](img215.png)
![$\displaystyle =\left[ \begin{array}{rrr}
0&-2&2\\
-10&0&4\\
0&0&2
\end{array}...
...=\left[ \begin{array}{rrr}
-8&1&2\\
-10&-5&13\\
-3&-3&3
\end{array} \right].
$](img216.png)
![$\displaystyle A=\left[ \begin{array}{rrr}
1&-2&0\\
0&3&-2
\end{array}\right],\;\; B=\left[ \begin{array}{rr}
1&2\\
-2&0
\end{array} \right].
$](img222.png)
![$\displaystyle BA= \left[ \begin{array}{rr}
1&2\\
-2&0
\end{array} \right]\cdot \left[ \begin{array}{rrr}
1&-2&0\\
0&3&-2
\end{array}\right]=
$](img225.png)
![$\displaystyle =\left[ \begin{array}{r\vert r\vert r}
\left[ \begin{array}{rr}
1...
...t]\cdot \left[ \begin{array}{r}
0\\
-2
\end{array}\right]
\end{array}\right]=
$](img226.png)
![$\displaystyle =\left[ \begin{array}{rrr}
1&4&-4\\
-2&4&0
\end{array} \right].
$](img227.png)
![$\displaystyle B^2=
\left[\begin{array}{rr}
1&2\\
-2&0
\end{array} \right] \cdo...
...}\right] \left[\begin{array}{r}
2 0
\end{array}\right]
\end{array}\right] =
$](img228.png)
![$\displaystyle =\left[ \begin{array}{rr}
1\cdot 1+2\cdot(-2)&1\cdot2+2\cdot 0 ...
...nd{array} \right]=
\left[ \begin{array}{rr}
-3&2\\
-2&-4
\end{array} \right].
$](img229.png)






![$ A=\left[ \begin{array}{rr}
3&1\\
2&1
\end{array} \right].
$](img239.png)


![$\displaystyle A^{-1}=\frac{1}{{\rm det} A}\left[ \begin{array}{rr}
A_{11}&A_{2...
...}
\end{array}\right]=\left[ \begin{array}{rr}
1&-1\\
-2&3
\end{array}\right].
$](img244.png)
![$\displaystyle 1)\;\;
A=\left[\begin{array}{rrr}
1&-1&1\\
-1&1&-1
\end{array} \...
...ay} \right],\;\;
C=\left[\begin{array}{rrr}
1&0&2\\
0&2&5
\end{array}\right];
$](img250.png)
![$\displaystyle 2)\;
A=\left[\begin{array}{rrr}
2&0&9\\
1&-1&0\\
0&5&-8
\end{ar...
...ht],\;
C=\left[\begin{array}{rrr}
8&0&1\\
0&-1&0\\
1&0&9
\end{array}\right].
$](img251.png)
![$\displaystyle 1)\; A=\left[ \begin{array}{rr}
0&2\\
-1&3
\end{array}\right], B...
...
\end{array}\right],B=\left[ \begin{array}{rr}
0&-1\\
1&0
\end{array}\right];
$](img252.png)
![$\displaystyle 3)\;A=\left[ \begin{array}{rrr}
2&-1&6\\
7&0&0\\
0&2&-1
\end{array}\right],\; B=\left[ \begin{array}{rrr}
1&0&-2\\
0&2&-8
\end{array}\right].
$](img253.png)
![$\displaystyle 1)\;A=\left[ \begin{array}{rr}
2&1\\
0&3
\end{array} \right], B...
...nd{array}\right], B=\left[ \begin{array}{rr}
1&0\\
0&-10
\end{array}\right].
$](img255.png)
![$\displaystyle 1)\;A=\left[ \begin{array}{rr}
5&0\\
-2&1
\end{array} \right], ...
...\end{array}\right], B=\left[ \begin{array}{rr}
9&0\\
0&1
\end{array}\right].
$](img259.png)


![$\displaystyle 1)\;\left[ \begin{array}{rr}
2&-1\\
3&5
\end{array} \right],\;
2...
...\;
4)\;\left[ \begin{array}{rrr}
5&0&1\\
-3&8&-1\\
0&2&1
\end{array}\right].
$](img262.png)